


Gravitons are the propagating modes associated with transverse, traceless
tensor metric perturbations, and they behave as a superposition of two
minimally coupled scalar fields, each corresponding to a polarisation state.
As a result, the graviton field, which is massless, has a spectrum of quantum
mechanical fluctuations similar to the one obtained for the scalar field
 . For each
polarisation state, the rms amplitude of the tensor metric
perturbations associated with a given Fourier mode at horizon crossing
is then (48)
. For each
polarisation state, the rms amplitude of the tensor metric
perturbations associated with a given Fourier mode at horizon crossing
is then (48)
where V is the volume associated with the Fourier expansion, and
the value of H is to be
calculated when the comoving scale k crosses outside the Hubble
radius during inflation.
The phases of the Fourier modes hk are again
independent and randomly distributed.
Consequently, the power spectrum at horizon re-entry,
Pt(k),
contains all the information necessary to describe the stochastic background
of gravitational waves generated during inflation. Again, in general,
Pt(k) can be approximated as a single power-law,
A scale-invariant power spectrum for the tensor perturbations then
corresponds to nt = 0.
For the simplest single-field inflationary models, as long as the
gravitational waves are
produced during the slow-roll phase, necessarily
nt
If a gravitational wave background produced during inflation was
detected using the CMBR,
and it was possible to estimate both the amplitude and spectral index of
the tensor perturbation
contribution to the CMBR temperature anisotropy and polarisation
signals, the next step would be to
try to detect locally those gravitational waves. If successful, such a
detection would
do much the same for the credibility of inflation as was achieved for
the Hot Big Bang theory itself by the detection of the CMBR.
The simplest quantity to compare with the experimental sensitivity of
gravitational wave detectors
is the present-day contribution per logarithmic interval of the
gravitational waves to the total energy density,
where
we then get in the case of a initial scale-invariant power spectrum of
gravitational waves
The shape of the initial power spectrum is broken at the scale of
matter-radiation equality,
keq = 6.22 x 10-2
Working within the simplest inflationary models, those which obey the
consistency relation
T/S
If the power spectrum of tensor perturbations is not a perfect power-law
there will be
small corrections to this expression, which will be in principle more
important for the
smallest scales, i.e. high k. A sensitivity of
Because the energy density in gravitational waves is proportional to the
rms strain 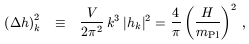
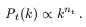
 0. Further,
under such
conditions, and in the simplest models, the ratio between
Pg(k) and
0. Further,
under such
conditions, and in the simplest models, the ratio between
Pg(k) and
 H2(k)
is approximately equal to
- nt/2, which is another way of stating the so-called
inflationary consistency relation
(56).
Note that in these models,
if the expansion of the Universe during inflation is perfectly
exponential, one gets
nt = 0, but then the amplitude of the tensor
perturbation also effectively tends to zero compared
with the amplitude of the (equally scale-invariant) scalar
perturbation. However, in
some slow-roll models with more complicated potentials, like
intermediate inflation, it is
possible to have an important tensor contribution to the perturbation
spectrum at horizon re-entry
though the power spectrum of density perturbations is scale-invariant.
H2(k)
is approximately equal to
- nt/2, which is another way of stating the so-called
inflationary consistency relation
(56).
Note that in these models,
if the expansion of the Universe during inflation is perfectly
exponential, one gets
nt = 0, but then the amplitude of the tensor
perturbation also effectively tends to zero compared
with the amplitude of the (equally scale-invariant) scalar
perturbation. However, in
some slow-roll models with more complicated potentials, like
intermediate inflation, it is
possible to have an important tensor contribution to the perturbation
spectrum at horizon re-entry
though the power spectrum of density perturbations is scale-invariant.
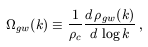
 c =
3H02 /
8
c =
3H02 /
8 G and
G and
 gw is the
energy density of the stochastic background
of gravitational waves with comoving wavenumber k. Given that
gw is the
energy density of the stochastic background
of gravitational waves with comoving wavenumber k. Given that
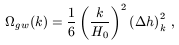
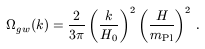
 0h2
0h2
 (3.36/g*)
Mpc-1, where g*
is the effective number of relativistic degrees of freedom (equals 3.36
for the standard cosmology
with 3 massless neutrino species), as gravitational waves that enter the
horizon prior to
matter-radiation equality redshift more slowly with time. Given that we
are only interested in
gravitational waves that can be detected locally, we will concentrate on
those which entered
the horizon during radiation domination. These correspond to
k << 2 x 10-24m,
or f << 10-16 Hz, where
f = c k / 2
(3.36/g*)
Mpc-1, where g*
is the effective number of relativistic degrees of freedom (equals 3.36
for the standard cosmology
with 3 massless neutrino species), as gravitational waves that enter the
horizon prior to
matter-radiation equality redshift more slowly with time. Given that we
are only interested in
gravitational waves that can be detected locally, we will concentrate on
those which entered
the horizon during radiation domination. These correspond to
k << 2 x 10-24m,
or f << 10-16 Hz, where
f = c k / 2 is
the frequency.
is
the frequency.
 -
7nt, and requiring the CMBR temperature anisotropies
detected on
large-angular scales by COBE to be reproduced, one obtains
(75)
-
7nt, and requiring the CMBR temperature anisotropies
detected on
large-angular scales by COBE to be reproduced, one obtains
(75)
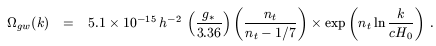
 gw(k)
h2 ~ 10-15 is therefore needed
for a serious search for local gravitational waves produced during
inflation. With its initial strain
detectors, the Earth-based LIGO (Laser Interferometer
Gravitational Wave Observatory) should be
able to identify a stochastic background of gravitational waves
provided
gw(k)
h2 ~ 10-15 is therefore needed
for a serious search for local gravitational waves produced during
inflation. With its initial strain
detectors, the Earth-based LIGO (Laser Interferometer
Gravitational Wave Observatory) should be
able to identify a stochastic background of gravitational waves
provided
 gwh2
is at
least a few times 10-3, at its most sensitive operating
frequency of roughly 100 Hz, with the
limit dramatically improving by possibly 6 orders of magnitude with more
advanced strain detectors installed in a later phase
(59).
Unfortunately, this misses the mark by six orders of magnitude.
gwh2
is at
least a few times 10-3, at its most sensitive operating
frequency of roughly 100 Hz, with the
limit dramatically improving by possibly 6 orders of magnitude with more
advanced strain detectors installed in a later phase
(59).
Unfortunately, this misses the mark by six orders of magnitude.
 h squared
times frequency squared, a detector operating at lower frequency has better
energy-density sensitivity for fixed strain sensitivity. Earth-based
detectors cannot operate at
frequencies below about 10 Hz because of seismic noise, but space-based
operators can. The
LISA (Laser Interferometer Space Antenna) mission has already
been approved by ESA, with an
initialy predicted launch date for only around 2020, but which may be
brought down to later this
decade if NASA gets interested in a joint effort. It will have a peak
sensitivity in terms of
h squared
times frequency squared, a detector operating at lower frequency has better
energy-density sensitivity for fixed strain sensitivity. Earth-based
detectors cannot operate at
frequencies below about 10 Hz because of seismic noise, but space-based
operators can. The
LISA (Laser Interferometer Space Antenna) mission has already
been approved by ESA, with an
initialy predicted launch date for only around 2020, but which may be
brought down to later this
decade if NASA gets interested in a joint effort. It will have a peak
sensitivity in terms of
 gwh2
of about 10-12 at a frequency close to 10-3 Hz
(59),
which is more promising, but still misses by at least three
orders of magnitude the required sensitivity level for the detection of
a local stochastic background
of inflationary produced gravitational waves. Also, at frequencies above
10-4 Hz it is expected
that the stochastic background of gravitational waves produced by
compact white-dwarf binaries will
swamp the inflationary signal. However, LISA may be able to
disentangle the two backgrounds, given
that it rotates in orbit and so it will be sensitive at different times
to regions in the Galactic plane, where the binaries are, and outside
(59).
gwh2
of about 10-12 at a frequency close to 10-3 Hz
(59),
which is more promising, but still misses by at least three
orders of magnitude the required sensitivity level for the detection of
a local stochastic background
of inflationary produced gravitational waves. Also, at frequencies above
10-4 Hz it is expected
that the stochastic background of gravitational waves produced by
compact white-dwarf binaries will
swamp the inflationary signal. However, LISA may be able to
disentangle the two backgrounds, given
that it rotates in orbit and so it will be sensitive at different times
to regions in the Galactic plane, where the binaries are, and outside
(59).