


3.1 The Method of Least Squares: Regression Analysis
The squares of the residuals are minimized; there is justification for this, and there is a long history and a vast literature (e.g. Williams 1959, Linnik 1961, Montgomery & Peck 1992).
For our particular example of fitting the ``regression line'', or a straight line y = ax + b through N pairs of (xi, yi), the solution to the least squares of the residuals in y yields
In the absence of knowledge of the how and why of a relation between
the xi and the yi any two-parameter
curve may be fitted to the data
pairs with simple coordinate transformations: for example
an exponential, y = b exp a,
requires yi to be
changed to ln yi in the above expressions;
a power-law, y = bxa;
change yi to ln yi and
xi to ln xi;
a parabola, y = b +
ax2; change xi to
(Note that the residuals cannot be Gaussian for all of these
transformations: of course it is always possible to minimize the
squares of the residuals, but it may well not be possible to retain
the formal justification for doing so.)
There are many further variations available. Algebra can provide
expressions for weighted data-pairs and/or the fitting of polynomials
of any order. For all of these, residuals can be examined to determine
which is the best way to model the data relations.
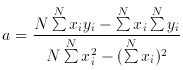 and
and
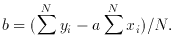
 xi.
xi.