


3.2 The Maximum-Likelihood (ML) Method
The maximum-likelihood method also has a long history: it was derived by Bernoulli in 1776 and by Gauss around 1821, and worked out in detail by Fisher in 1912.
Consider the probability density function F (x;  ), x a random
variable,
), x a random
variable,  a single parameter
characterizing the known form of F. We
want to estimate
a single parameter
characterizing the known form of F. We
want to estimate  . Let
x1, x2, . . , xN
be a random sample of size N, the
xi independent and drawn from the same
population. Then the so-called
``likelihood function'' is the joint probability density function
. Let
x1, x2, . . , xN
be a random sample of size N, the
xi independent and drawn from the same
population. Then the so-called
``likelihood function'' is the joint probability density function
This is the probability, given
Note that traditionally it is ln L that is maximized. It should be
pointed out that the maximum of the function cannot always be
determined by this method - finding the ML time of occurrence of a
singular observed event is a case in point.
The MLE is a statistic with many highly desirable properties - it is
efficient, usually unbiased, it has minimum variance, and it is ~
Normally distributed.
If the residuals are Normally distributed, then minimizing the sum
of squares (Section 3.1) is the
maximum-likelihood method.
By way of example,
Jauncey (1967)
showed that ML was an excellent
way of estimating the slope of the number - flux-density relation for
extragalactic radio sources, and this particular application has made
the technique familiar to astronomers. The source count is assumed to
be of the power-law form
where N is the number of sources on a particular patch of sky with
flux densities greater than S, k is a constant and
where
and
Differentiation of this with respect to
However, with a computer handy it is simplest to forget the
differentiation and to evaluate L (
This application of ML makes optimum use of the data in that the
sources are not grouped and the loss of power that always results from
binning is avoided.
To return to general considerations, after the ML estimate has been
obtained, it is essential to perform a final check - does the MLE
model fit the data reasonably? If it does not then the data are
erroneous when the model is known to be right; conversely, the adopted
or assumed model is wrong. There are many ways of carrying out such a
check: two of these, the chisquare test and the Kolmogorov-Smirnov
test, are described in Section 4.2.
The ML procedure may be generalized to obtain simultaneous MLEs of
several parameters:
and the solution of these simultaneous equations yields the MLE
It is important to emphasize the ML principle, which is that when
confronted with the choice of hypotheses, choose that which maximizes
L, i.e. the one giving the highest probability to the observed
event. This sounds reasonable, but in fact the proofs of certain
theorems (see e.g.
Martin 1971)
concerning the ``goodness'' of MLEs are
required to justify the procedure.

 , of obtaining the observed set of
results. The maximum-likelihood estimator (MLE) of
, of obtaining the observed set of
results. The maximum-likelihood estimator (MLE) of  is
is 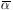 = (that
value of
= (that
value of  that maximizes
L (
that maximizes
L ( ) for all variations
of
) for all variations
of  ), i.e.
), i.e.


 is the exponent,
or slope in the log N-log S plane, which we wish to
estimate. If we
consider M sources with flux densities S in the range
S0 to Smax, then
a straightforward application of the ML procedure above yields the
following likelihood function:
is the exponent,
or slope in the log N-log S plane, which we wish to
estimate. If we
consider M sources with flux densities S in the range
S0 to Smax, then
a straightforward application of the ML procedure above yields the
following likelihood function:



 then yields the equation from which
then yields the equation from which 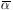 , the MLE of
, the MLE of  , is obtained:
, is obtained:

 ) over a wide range of
) over a wide range of  , small
, small 
 .
Maximum L yields
.
Maximum L yields 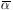 ,
while a good estimate of the standard deviation in
,
while a good estimate of the standard deviation in
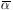 is obtained
from the two
values of
is obtained
from the two
values of  that cause L
to drop by e1/2
from its maximum, the factor e1/2 because the asymptotic
distribution of L is Gaussian. For large M and b
(Jauncey 1967),
that cause L
to drop by e1/2
from its maximum, the factor e1/2 because the asymptotic
distribution of L is Gaussian. For large M and b
(Jauncey 1967),


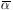 i.
i.