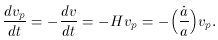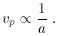1. The Hubble Law and Particle Kinematics
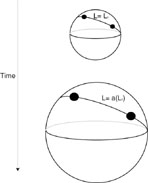
The Hubble law (1) is a direct result of the CP. Consider the expansion of the universe, which must occur in a homogeneous and isotropic manner according to the CP. The expansion can be visualized with the analogy of a balloon with a grid painted on it. Of course this should not be taken literally, since the spatial extent of the universe is three dimensional. Think of the grid as a network of meter sticks and clocks at rest with respect to the Hubble expansion, which corresponds to the Cosmic Rest Frame (CRF) mentioned earlier. Due to the expansion, two particles (10) initially separated by a distance l0, will be separated by a distance l(t) = a(t) l0 at some later time t, see Figure (2). Because of the CP, the function a(t), known as the scale factor, can only be a function of time. From this relation, the speed of the observers relative to each other is,
where
Figure 2. As the universe expands the
distance between galaxies
(test particles) increases proportional to the scale factor,
L(t) = a(t) L0
From this derivation of the Hubble law, it becomes manifest that
the Hubble Constant can depend on time. In this new way of
defining H(t) =
To understand how particles `come to rest' in the CRF, consider a
particle starting out with a peculiar velocity vp >>
c. The
particle passes a CRF observer (O1) at time t
and travels a
distance dl = vp dt. At this time the
particle passes
another CRF observer (O2), who has a velocity dv =
Hdl = Hvp dt relative to
O1. O2 measures the particle's
peculiar velocity as, vp(t + dt) =
vp(t) - dv. This shows
that the peculiar velocity satisfies the equation of motion,
Solving this differential equation yields,
This indicates that the peculiar
velocity decreases as the scale factor increases. Indicating that
as the universe expands, particles with peculiar velocities tend
to go to zero meaning they `settle' into the CRF.
10 Remember that when one speaks of a
cosmological
model, the test particles are galaxies. Back.
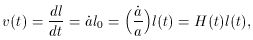
is the time derivative of
the scale factor.
(t)
/ a(t), H(t) measures the rate of
change of the scale factor, a(t), and offers a way to link
observations (like Hubble's) with a proposed model using the scale
factor. For Hubble's observations, the distance l(t) was small
and H(t) could be estimated by a linear relation yielding
equation (1).
