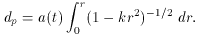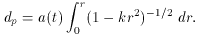2. The Robertson Walker Metric
The only metric compatible with Hubble's findings and the Cosmological Principle is the Robertson Walker Metric (RWM) with the corresponding line element,
For a brief explanation consider the following:
There are a few subtleties that must be discussed. First, the r
that appears in the line element (4) is not
the radius of the universe. The r is a dimensionless, comoving
coordinate that ranges from zero to one for k = 1. The measurable,
physical distance is given by the RWM above. Choosing a frame
common to two distinct points, one obtains,
for their
separation. Where d
Evidently for a k = 0 flat universe, the distance is simply,
Thus, a(t) has units of length and depends on the geometry of
the spacetime.
The next issue is that of curvature. The curvature of the
universe is determined by the amount of energy and matter that is
present. The space is one of constant curvature determined by the
value of k. Because any arbitrary scaling of the line element
(4) will not affect the sign of k, we have the
following convention (11)
11 When the metric is invariant under
multiplication by a scale factor, the metric is said to be
conformally invariant. Back.
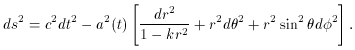
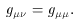
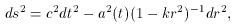
 and
d
and
d are zero, because one has
freedom to arrange the axis and ds2 represents their
separation in spacetime. Thus, their spatial separation is found
by considering spacelike hypersurfaces, that is dt2 =
0. Thus, their separation is
are zero, because one has
freedom to arrange the axis and ds2 represents their
separation in spacetime. Thus, their spatial separation is found
by considering spacelike hypersurfaces, that is dt2 =
0. Thus, their separation is