


In past years, inflation has become more of a scenario than model. A plethora of models have been suggested, all of which share the common feature that the universe goes through a brief period of rapid expansion. This rapid expansion is manifested in the evolution of the scale factor, a(t). In the case of inflation, a(t) ~ tn, where n > 1 and the universe expands faster than light. This does not violate relativity, since the spacetime is the thing expanding (i.e., no information is being transferred). Since n can take on any value greater than one, this is already an example of the flexibility of the theory.
In Section 2 it was shown by Equation
(14) that if an
equation of state p =
- is achieved and one
has a positive
cosmological constant, then the universe will accelerate.
Incorporating the cosmological constant,
is achieved and one
has a positive
cosmological constant, then the universe will accelerate.
Incorporating the cosmological constant,
 , into an energy
density,
, into an energy
density, 
 , and assuming it is the
dominate one can use (15) and (16) to obtain,
, and assuming it is the
dominate one can use (15) and (16) to obtain,
One can choose to ignore the curvature term, since one anticipates
a large increase in the scale factor. That is, the presence of
the scale factor in the denominator of the -k/a2 term in
the equation above will leave this term negligible. This is often
referred to as the redshifting of the curvature, since the effect
of the curvature can be ignored if the scale factor becomes large
enough during a period of constant energy density
This is a differential equation with the solution,
where H = (8/3
Since
So given a constant vacuum term, the DeSitter scenario `drives'
the universe to a flat geometry, thus approaching
The revision of this idea was suggested by Guth in the early
1980's [33],
[34]. The crux
to the modern
inflationary scenario, in contrast to the DeSitter model, is to
limit the amount of time that this rapid expansion (inflation)
occurs. Guth explained the physical mechanism for such an
inflationary period as corresponding to a phase transition in the
early universe. By limiting the time of the quasi-exponential
expansion, Guth was able to produce a universe more like our own.
Unlike DeSitter's model, which was based on a pure solution to
Einstein's equations, Guth's idea was based on ideas from particle
physics. Guth was studying a class of grand unified theories
(GUTs) and the predictions they make about particle production in
the universe. This suggested how cosmology could be united with
particle physics in a phenomenological manner, which has become
one of the most appreciated beauties in modern physics today.
18 Not to be confused with
the Einstein-DeSitter model. Back.
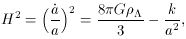

 . This is actually a glimpse
of how the flatness
problem will be resolved. So, ignoring the curvature term, we have
. This is actually a glimpse
of how the flatness
problem will be resolved. So, ignoring the curvature term, we have
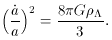
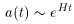
 G
G

 )1/2 and
since
)1/2 and
since 
 is a constant, so is
H. This model is
referred to as the DeSitter model
(18)
By introducing a negative pressure,
the flatness problem is solved. The crux of this argument is that
is a constant, so is
H. This model is
referred to as the DeSitter model
(18)
By introducing a negative pressure,
the flatness problem is solved. The crux of this argument is that

 is a
constant (19)
This comes
from the fact that
is a
constant (19)
This comes
from the fact that 
 is
an intrinsic property of
the spacetime manifold. As the manifold is stretched, this vacuum
energy does not change. Another way this can be explained is by
that the Einstein equations are arbitrary up to a constant term
is
an intrinsic property of
the spacetime manifold. As the manifold is stretched, this vacuum
energy does not change. Another way this can be explained is by
that the Einstein equations are arbitrary up to a constant term
 . The disadvantage of this
explanation is that it does
not manifest the connection between cosmology and particle theory
(more on this later).
. The disadvantage of this
explanation is that it does
not manifest the connection between cosmology and particle theory
(more on this later).

 is taken to be the dominate
form of energy,
the other contributions to the density in the Friedmann equation
(28) are also redshifted away, since
is taken to be the dominate
form of energy,
the other contributions to the density in the Friedmann equation
(28) are also redshifted away, since
 M
~ a-3,
M
~ a-3,
 R ~
a-4. This leads to the
conclusion that no matter what the initial distribution of
R ~
a-4. This leads to the
conclusion that no matter what the initial distribution of
 T =
T =
 M +
M +
 R +
R +

 , the vacuum energy
will eventually dominate. Thus, the assumption of
, the vacuum energy
will eventually dominate. Thus, the assumption of

 domination can actually be
relaxed.
domination can actually be
relaxed.
 =
=
 c,
where
c,
where  c is
the critical density, (i.e.,
c is
the critical density, (i.e.,
 c =
(3H2) / (8
c =
(3H2) / (8 G). This evolution, if allowed to
continue, will produce an empty universe with practically no
radiation or matter. The fact that we live in a universe that is
full of matter and radiation is why the original proposal, by
DeSitter, was rejected and forgotten.
G). This evolution, if allowed to
continue, will produce an empty universe with practically no
radiation or matter. The fact that we live in a universe that is
full of matter and radiation is why the original proposal, by
DeSitter, was rejected and forgotten.
19 Actually,
 does
not have to be a constant; in-fact, it can be a function of time.
Such vacuum energies are referred to as Quintessence, or Dark
energy, and are the subject of much research. Unfortunately, time
will not permit a discussion
([30]
[31],
[32]).
Back.
does
not have to be a constant; in-fact, it can be a function of time.
Such vacuum energies are referred to as Quintessence, or Dark
energy, and are the subject of much research. Unfortunately, time
will not permit a discussion
([30]
[31],
[32]).
Back.