


B. Inflation As a Solution to the Initial Value Problems
It was discussed in the first part of this section that inflation
solves the flatness problem because the universe expands at such a
great rate that the curvature term is `redshifted' away. Another
way of stating this result is to define inflation as any period in
the evolution of the universe in which the scale factor (a(t))
undergoes a period of acceleration; i.e.,
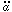 (t)
> 0. This condition can be used to provide a further insight
into what inflation means. Consider the quantity (H a)-2.
Knowing
(t)
> 0. This condition can be used to provide a further insight
into what inflation means. Consider the quantity (H a)-2.
Knowing
it follows that
Now consider the time derivative of this
quantity.
given the conditions
Referring back to equation (45), and dividing
through by H2, one again gets the equation for the evolution
of the density parameter,
Comparing Equations (48) and (49)
expresses the fact that the curvature decreases during inflation.
More explicitly, as a and H increase by tremendous amounts
during inflation, the right had side of (49)
approaches zero since the denominator becomes large. Thus,
But (48) can also be written as, d(1/Ha)/dt < 0
since H
and a are both taken as positive quanitites. Recall that 1/H
gives the particle horizon of a flat universe, so one can use
Equation (5),
where r is the
comoving radial coordinate. Using d(1/Ha)/dt < 0 gives the
relation,
What does this mean? This implies that during a period of
inflation the comoving frame (parameterized by r,
Notice it is now justified to use the flat universe approximation,
since inflation forces
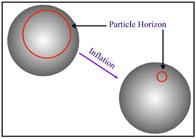
Figure 4. This figure illustrates the more
natural perspective
contrasted to that of Figure (3). The frame of
reference is that of comoving coordinates, which puts the observer
at rest relative to the expansion. In this frame the particle
horizon is seen to shrink.
So, the picture during inflation is that the spacetime background
expands at an accelerating pace. This resolves the horizon
problem, since causal regions in the early universe are stretched
to regions much larger than the Hubble distance. This is because
during inflation the scale factor evolves at super-luminal speeds,
whereas the particle horizon (Hubble distance) is approximately
constant. The particle horizon does expand at the speed of light
(by definition), but this pales in comparison to the evolution of
the scale factor. Remember the Hubble distance is the farthest
distance light could have traveled from a source to reach an
observer. Once inflation ends, the scale factor returns to its
sub-luminal evolution leaving the particle horizon to ``catch
up''. This situation is illustrated in Figure 5. So as
we look out at the sky today we are still seeing the regions of
uniformity that were stretched outside the particle horizon during
inflation.
A more quantitative argument is given by considering the physical
distance light can travel during inflation compared to after.
where tinf marks the beginning of inflation,
trec is the time of recombination, and
t0 is today.
Equation (50) can be understood by making the following
estimates. In the first integral, the scale factor during
inflation is given by, a(t) ~ eHt. Whereas, in
the second
integral one can assume the scale factor is primarily matter
dominated a(t) ~ t2/3. Furthermore, the
integral on the
right can be simplified by taking trec = 0. Of course
this only
increases the integral. Lastly, tinf can be set equal to
zero and then trec =
Evaluating the integrals and a bit of algebra gives,
where the last step uses H =
With the discussion presented thus far, the monopole problem is
solved trivially. The number of predicted monopoles per particle
horizon at the onset of inflation is on the order of one
[42].
As discussed previously, this would result in a
density today that would force
This holds true for the other topological defects and unwanted
relics associated with spontaneous symmetry breaking (SSB) in
unified theories. This leads one to ask, why would the temperature
increase after inflation? The mechanism by which this reheating
of the universe takes place is related to the mechanisms that
bring about the demise of the inflationary period. These
mechanisms are understood through the dynamics of scalar fields,
to be discussed in the next section.
One question has been left unresolved with reference to the
problems of initial values in the hot Big Bang model. This is the
problem of the origin of structure in the universe. It was
pointed out that the DeSitter universe is left empty and cold with
no stars or galaxies. The flatness and monopole problem were
resolved by a redshifting of the various energy densities. But, if
no energy is present, how can particle creation take place? This
peculiar feature of inflation will be discussed in the next
section, but here I would like to present a qualitative
description.
At the end of inflation, all energy densities have become
negligible except the vacuum density (or cosmological constant if
you prefer). Where did the energy go? It went into the
gravitational `potential' of the universe, so energy is still
conserved [43],
[44]
(24)
Thus, at the end of inflation
there is a universe filled with vacuum energy, which takes the
form of a scalar field. This scalar field is coupled to gauge
fields, such as the photon. As the scalar field releases its
energy to the coupled field, the universe goes through a reheating
phase where particles are created as in the hot Big Bang model.
The energy for this particle creation is provided by the `latent'
heat locked in the scalar field. More will be said on this later,
but the important point is that the hot Big Bang model picks up
where inflation leaves off. Thus, one may be inclined to say,
inflation is a slight modification to the hot Big Bang model. One
author refers to inflation as, ``a bolt on accessory''
[29].
This all sounds very appealing, however reheating is a fragile
topic for inflation and results in a number of different models.
This derives from the fact that if the temperature is too high at
the time of reheating, the unwanted particle relics could be
re-introduced into the model! As a result, many different
reheating scenarios have been proposed, along with many different
models for the onset of inflation.
One surprise from inflation makes all of this worry worth it.
Along with offering a solution to the various initial value
problems of the hot Big Bang, inflation offers a mechanism to seed
the large-scale structure of the universe. Depending on the model
chosen, (e.g., reheating temperature, onset conditions, etc.) one
gets predictions for the large-scale structure of the universe and
the anisotropies in the cosmic background. As will be seen in the
next section, this again demonstrates how the very small (quantum
mechanics) can impact the very large (universal structure). In
some models of inflation, a small fluctuation in the quantum foam
of the Planck epoch (t < 10-43) can give rise to the
formation
of galaxies, solar systems, and eventually human life! We are the
result of pure chance! This is getting a little ahead of the game,
so let us consider a quantitative and mechanical explanation of
inflation.
24 Actually, energy
need not be conserved if we live in an open universe. However,
this need not concern us here. Back.
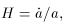
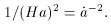
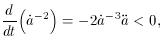
 > 0 and
> 0 and
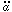 > 0. This implies,
> 0. This implies,

 =
=  /
/
 c,
c,
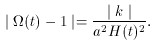
 is driven towards one and the
universe is made flat by
inflation. As the scale factor evolves under the condition
is driven towards one and the
universe is made flat by
inflation. As the scale factor evolves under the condition
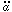 > 0 the density
(
> 0 the density
( ) approaches the critical
density (
) approaches the critical
density ( c).
c).
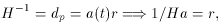
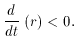
 ,
and
,
and  ), SHRINKS! Remember that the comoving
coordinates represent the system of coordinates that are at rest
with respect to the expansion. In other words, instead of viewing
the spacetime as expanding it is equally valid to view the
particle horizon as shrinking. To visualize this, it is perhaps
useful to again consider the idea of an expanding balloon (see
Figures 3 and
4). Normally, in this
example, one views two points on the surface of the balloon as
getting farther apart because the balloon is expanding. However,
if one chooses a frame in which the surface is not expanding this
would mean that the metric, or way of measuring, would shrink.
Thus, the distance between the points would get larger, since the
comoving coordinates got smaller. Each frame of reference has its
advantages. For the remainder of this paper I will choose the
frame where the universe is seen to expand. This has the
advantage that the Hubble length remains `almost' constant during
inflation, which eases the discussion in the analysis to follow.
), SHRINKS! Remember that the comoving
coordinates represent the system of coordinates that are at rest
with respect to the expansion. In other words, instead of viewing
the spacetime as expanding it is equally valid to view the
particle horizon as shrinking. To visualize this, it is perhaps
useful to again consider the idea of an expanding balloon (see
Figures 3 and
4). Normally, in this
example, one views two points on the surface of the balloon as
getting farther apart because the balloon is expanding. However,
if one chooses a frame in which the surface is not expanding this
would mean that the metric, or way of measuring, would shrink.
Thus, the distance between the points would get larger, since the
comoving coordinates got smaller. Each frame of reference has its
advantages. For the remainder of this paper I will choose the
frame where the universe is seen to expand. This has the
advantage that the Hubble length remains `almost' constant during
inflation, which eases the discussion in the analysis to follow.
 = 1 by
the fact that 1/a2 H2
increases so rapidly compared to k in Equation
(49). Also note that
= 1 by
the fact that 1/a2 H2
increases so rapidly compared to k in Equation
(49). Also note that
 doesn't have to be
entirely matter dominated. For example,
doesn't have to be
entirely matter dominated. For example,
 =
=
 M +
M +

 = .3 + .7 = 1 is an acceptable
configuration in the inflation scenario.
= .3 + .7 = 1 is an acceptable
configuration in the inflation scenario.
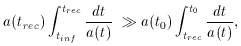
 t is the time inflation lasts.
Thus,
t is the time inflation lasts.
Thus,
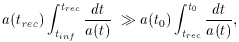

 /a = 2/3t. So, we
can see from
(51) that as long as inflation lasts long enough
(
/a = 2/3t. So, we
can see from
(51) that as long as inflation lasts long enough
( t) then the horizon
problem is solved.
t) then the horizon
problem is solved.
 >> 1, which is not
observed. As stated previously, the comoving (causal) horizon
shrinks during inflation. Thus, if the universe starts with one
monopole, it may contain that one monopole after inflation, but no
more. However, this is highly unlikely if the universe inflates by
an appreciative amount. Furthermore, inflation redshifts all
energy densities. So, as long as the temperature does not go near
the critical temperature after inflation, no additional monopoles
may form.
>> 1, which is not
observed. As stated previously, the comoving (causal) horizon
shrinks during inflation. Thus, if the universe starts with one
monopole, it may contain that one monopole after inflation, but no
more. However, this is highly unlikely if the universe inflates by
an appreciative amount. Furthermore, inflation redshifts all
energy densities. So, as long as the temperature does not go near
the critical temperature after inflation, no additional monopoles
may form.