


C. Inflation and Scalar Fields
As stated above, inflation is capable of solving many of the
initial value, or `fine-tuning', problems of the hot Big Bang
model. This is assuming that there is some mechanism to bring
about the negative pressure state needed for quasi-exponential
growth of the scale factor. In the early 1980's, Alan Guth
[33]
was studying properties of grand unified theories or
GUTs. He noticed that these theories predict a large number of
topological defects. Specifically, he was addressing the issue of
monopole creation in the SU(5) GUT. He found the theory predicts a
large number of these monopoles, and that they should `over-close'
the universe. This means that the monopole contribution to
 is greater than the observed
upper-bound on the density
parameter,
is greater than the observed
upper-bound on the density
parameter,  > 4, which comes from observation
[5]. To remedy this,
Guth concluded that the symmetry breaking associated with scalar
fields in the particle theory must cause the universe to enter a
period of rapid expansion. This expansion `dilutes' the density
of the monopoles created, as stated above.
> 4, which comes from observation
[5]. To remedy this,
Guth concluded that the symmetry breaking associated with scalar
fields in the particle theory must cause the universe to enter a
period of rapid expansion. This expansion `dilutes' the density
of the monopoles created, as stated above.
The first step in understanding the dynamics of scalar fields is
to undertake the study of field theory. In field theory, one
considers a Lagrangian density, as opposed to the usual Lagrangian
from classical mechanics. This is because the scalar field is
taken to be a continuous field, whereas the Lagrangian in
mechanics is usually based on discrete particle systems. The
Lagrangian (L) is related to the Lagrangian density
( ) by,
) by,
Usually the scalar field is represented by a continuous function,
The resulting Euler-Lagrange equations result from varying the
action with respect to spacetime
[41],
where xµ = (t, -xi) as
usual, and
The prime represents differentiation with respect to
Thus, the inhomogeneities in the field are
redshifted away during inflation since the scale factor increases
by a large amount.
One can also define the stress-energy tensor by use of Noether's
theorem [41],
This is useful, because it can be compared to
Tµ
The calculation for the pressure is a bit more subtle,
Consider the first component of pressure, again making use of
(53) and (57),
Since g11 = -1 and one can use the metric to raise
and lower indices,
Since the metric is diagonal this yields,
Similarly, the T22 and T33
components may be found. So for the total pressure one finds,
or,
From the T00 component we already found,
Equations (58), (59) for the pressure and
the energy density, show that the equation, p =
-
The first term 1/2
By plugging in the energy density of the field (61)
and making use of the Friedmann equation (to get H) one obtains
Equation (55) in perhaps a more enlightening way.
From the pressure and energy density derived above, we see that
the requirement that p =
-
At this point, it is useful to distinguish
However, observation of the large-scale structure of the universe
and anisotropies in the cosmic background should be able to
constrain the inflaton parameters to a particular region. This
can then be used by particle theorists, as a motivation for some
required scalar field. Observational aspects of inflation will be
considered in the next section, but this property of the inflaton
field manifests itself as one of the greatest contributions of
cosmology commensurate with particle theory. Some examples of
potentials that have been proposed for the inflaton are presented
below [47],
[29].
In Guth's original inflation scenario
[33],
the inflaton
field (
Tunneling that leads to bubble nucleation is a first order phase
transition. This is very similar to processes that take place in
the study of condensed matter physics, fluid dynamics, and
ferromagnetism (see for example
[48] and
[49]).
The bubbles experience a state of negative pressure. Once
created, they continue to expand at an exponential rate. Each
expanding bubble corresponds to an expanding domain. However, when
one carefully investigates this situation, one finds that the
bubbles can collide as they reach the false vacuum. Furthermore,
the size of these bubbles expands at too great of a rate and the
corresponding universe is left void of structure. One finds that
too much inflation occurs and the visible universe is left empty.
This is referred to as the `graceful exit' problem. Again one is
presented with an empty universe, which was the same reason that
the DeSitter universe idea was abandoned.
Guth and others further tried to remedy these problems by
fine-tuning the bubble formation. The problem with this is two
fold. One, cosmologists and particle theorists don't like
fine-tuning. The idea is to form a model that gives our universe
as a usual result that follows from natural consequences. By
natural one means that the scales of the model are related to the
fundamental constants of nature; e.g., quantum gravity should
occur at the Planck scale, since this scale is the only one
natural in units (c,
In 1982, a solution to the graceful exit problem was proposed by
Linde [50]
and independently by Steinhardt and Albrecht
[51].
This New Inflation model solves the
graceful exit problem by assuming the inflaton field evolves very
slowly from its initial state, while undergoing a phase transition
of second order. Figure 8 illustrates this by again
considering the evolution of
The majority of current models rely on another concept coined by
Linde as Chaotic Inflation. This model differs from Old and
New Inflation in that no phase transitions occur. In this scenario
the inflaton is displaced from its true vacuum state by some
arbitrary mechanism, perhaps quantum or thermal fluctuations.
Given this initial state, the inflaton slowly rolls down the
potential returning to the true vacuum (see
Figure 9). This model has the advantage that no
fine-tuning
of critical temperature is required. This model presents a
scenario, which can be fulfilled by a number of different models.
Figure 9. Toy Model For Chaotic Inflation -
The inflaton finds
itself displaced from the true vacuum and proceeds to `roll' back.
Inflation takes place while the inflaton is displaced.
After the displacement of the inflaton, the universe undergoes
inflation as the inflaton rolls back down the potential. Once the
inflaton returns to its vacuum (true) state, the universe is
reheated by the inflaton coupling to other matter fields. After
reheating, the evolution of the universe proceeds in agreement
with the Standard Big Bang model.
Although the inflaton could in principle be displaced by a very
large amount, all the inflationist need be concerned with is the
last moments of the evolution. This is when the perturbations in
the scalar field are created that eventually lead to large-scale
structure and anisotropies in the cosmic background. As long as
the inflaton is displaced by a minimal amount (minimal to be
defined in a moment) the initial value problems will be solved.
When considering quantum fluctuations resulting in the
displacement of
Successful evolution is only possible if
V(
This method is successfully used in a number of inflationary
models that make predictions in accordance with observation. It
must be stated again that Chaotic Inflation results in a very
general theory. The inflaton field originally proposed by Guth's
model was that of a grand unified theory, but within the Chaotic
Inflationary scenario any inflaton field can be used that
satisfies the SRA. With these general requirements, potentials
used in supergravity, superstrings, and supersymmetry theories can
be used to motivate inflation.
Using the energy density obtained in equation (61) one
can restate the Friedmann equation (45) in terms of the scalar field.
Also, the equations of motion derived in (55) are
restated here for convenience.
Using the SRA, one can simplify these equations by
eliminating the
where Mp is the Planck mass and has been substituted
for G,
remembering that
One can use equations (72) and (73) to manifest
the connection between the slow-roll condition (69)
and the generic definition of inflation, that is
For inflation to take place means
Using (72) and differentiating with respect to time,
Plugging this result into (74) gives,
Solving (73) for
Lastly, substituting H2 from (72) one obtains,
But this is just the slow-roll condition
25 In much of the literature on
inflation, the slow-roll approximation is presented as a necessary
and sufficient condition for inflation. However, in many new
models of inflation this is not necessary. For a treatment of
these models, see
[43],
[44],
[45, and
references therein]. Back.
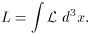
 (x, t), which can be real or
complex. Given a potential
density of the field, V(
(x, t), which can be real or
complex. Given a potential
density of the field, V( ),
),
 takes the form,
takes the form,
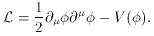
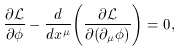
 = c = 1. Also note,
gµ
= c = 1. Also note,
gµ = diag(1,
-1, -1, -1), the factor of
= diag(1,
-1, -1, -1), the factor of  -g
that usually appears in the action and other equations involving
tensor densities will be sqrt[-(-1)] = 1 (Minkowski space). The
resulting equation is
-g
that usually appears in the action and other equations involving
tensor densities will be sqrt[-(-1)] = 1 (Minkowski space). The
resulting equation is
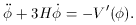
 and
the term containing the Hubble constant serves as a kind of
friction term resulting from the expansion. The field is taken to
be homogeneous, which eliminates any gradient contributions. This
homogeneity is a safe assumption, since physical gradients
are related to comoving gradients by the scale factor,
and
the term containing the Hubble constant serves as a kind of
friction term resulting from the expansion. The field is taken to
be homogeneous, which eliminates any gradient contributions. This
homogeneity is a safe assumption, since physical gradients
are related to comoving gradients by the scale factor,


 for a
perfect fluid, namely,
for a
perfect fluid, namely,

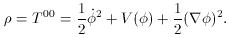
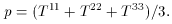
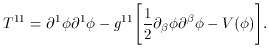
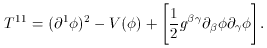
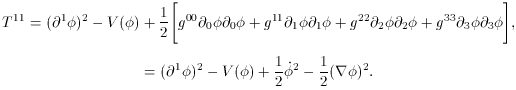
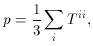
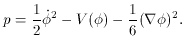
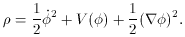
 is not quite
satisfied. A first resolution to this problem is to again assume
that the scalar field (
is not quite
satisfied. A first resolution to this problem is to again assume
that the scalar field ( ) is
spatially homogeneous, allowing
one to eliminate the gradient terms
(
) is
spatially homogeneous, allowing
one to eliminate the gradient terms
(
 ). This
assumption is only made at this point to simplify the analysis. As
we have seen if one keeps the terms, it can be shown that the
gradients are redshifted away by the expansion (56).
Ignoring gradients, the equations become
). This
assumption is only made at this point to simplify the analysis. As
we have seen if one keeps the terms, it can be shown that the
gradients are redshifted away by the expansion (56).
Ignoring gradients, the equations become
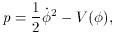
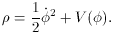
 2 can be thought of as
the kinetic energy and the second as the potential, or
configuration energy. It is now possible to explicitly see where
Equation (55) came from if we assume the field can
be described as a `perfect' fluid. This assumption allows us to
use a continuity equation,
2 can be thought of as
the kinetic energy and the second as the potential, or
configuration energy. It is now possible to explicitly see where
Equation (55) came from if we assume the field can
be described as a `perfect' fluid. This assumption allows us to
use a continuity equation,
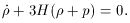
 can be
approximately met, if one
requires
can be
approximately met, if one
requires  <<
V(
<<
V( ). This leads to what is
called the
slow-roll approximation (SRA), which provides a natural condition
for inflation to occur
(25)
To assure the constraint on
). This leads to what is
called the
slow-roll approximation (SRA), which provides a natural condition
for inflation to occur
(25)
To assure the constraint on
 , one must also require that
, one must also require that
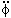 be
negligible. Given these requirements, we will to define the
slow-roll parameters and introduce the Planck mass
(26)
[46],
be
negligible. Given these requirements, we will to define the
slow-roll parameters and introduce the Planck mass
(26)
[46],

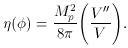
 as the inflaton
field. Inflaton is the name given to
as the inflaton
field. Inflaton is the name given to
 , since its origin does
not have to originate with a specified particle theory. Although
the original hope was that
, since its origin does
not have to originate with a specified particle theory. Although
the original hope was that  would
help determine the correct
particle physics models, current model building does not
necessarily require specific particle phenomenology. This is
actually an advantage for inflation, it retains its power to solve
the initial value problems, yet it could arise from any arbitrary
source (i.e., any arbitrary inflaton).
would
help determine the correct
particle physics models, current model building does not
necessarily require specific particle phenomenology. This is
actually an advantage for inflation, it retains its power to solve
the initial value problems, yet it could arise from any arbitrary
source (i.e., any arbitrary inflaton).
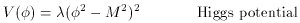



 ) sits at a local minimum
and is trapped in a false
vacuum state (see Figure 7). The vacuum state of
a field
or particle is the lowest energy state available to the system.
Some examples are the ground state of the hydrogen atom (-13.6 eV)
and the ground state of the harmonic oscillator (1/2
) sits at a local minimum
and is trapped in a false
vacuum state (see Figure 7). The vacuum state of
a field
or particle is the lowest energy state available to the system.
Some examples are the ground state of the hydrogen atom (-13.6 eV)
and the ground state of the harmonic oscillator (1/2

 ). The concept of `false'
vacuum comes from examination of
Figure 7. If
). The concept of `false'
vacuum comes from examination of
Figure 7. If
 is `placed' in the potential well on
the left, the lowest energy available is that of the false vacuum.
The only way
is `placed' in the potential well on
the left, the lowest energy available is that of the false vacuum.
The only way  can get out of this
local minimum is by
quantum tunneling, after some characteristic time. As tunneling
takes place the universe inflates. Inflation halts when
can get out of this
local minimum is by
quantum tunneling, after some characteristic time. As tunneling
takes place the universe inflates. Inflation halts when
 reaches the false vacuum and bubbles of the false vacuum coalesce
releasing the `latent' heat that was stored in the field. This is
much like the way bubble nucleation occurs when opening a bottle
of compressed liquid (like soda). Energy escapes from the soda in
the form of carbon dioxide and the liquid enters a lower more
favorable energy state.
reaches the false vacuum and bubbles of the false vacuum coalesce
releasing the `latent' heat that was stored in the field. This is
much like the way bubble nucleation occurs when opening a bottle
of compressed liquid (like soda). Energy escapes from the soda in
the form of carbon dioxide and the liquid enters a lower more
favorable energy state.
 ,
G). Secondly, if the model is
fine-tuned to agree with the observations of the anisotropies in
the cosmic background, the bubbles would collide far too often.
This results in the appearance of topological defects, like the
monopoles. However, this was the whole reason inflation was
invoked in the first place.
,
G). Secondly, if the model is
fine-tuned to agree with the observations of the anisotropies in
the cosmic background, the bubbles would collide far too often.
This results in the appearance of topological defects, like the
monopoles. However, this was the whole reason inflation was
invoked in the first place.
 . If
. If
 `rolls' down the
potential at a slow rate, one obtains the amount of inflation
needed to solve the initial value problems. After the universe
cools to a critical temperature, Tc,
`rolls' down the
potential at a slow rate, one obtains the amount of inflation
needed to solve the initial value problems. After the universe
cools to a critical temperature, Tc,
 can proceed to
its `true' vacuum state energy. The transition of the potential
is a second order phase transition, so this model does not require
tunneling [42].
This type of transition is similar to
the transitions that occur in ferromagnetic systems
[49].
can proceed to
its `true' vacuum state energy. The transition of the potential
is a second order phase transition, so this model does not require
tunneling [42].
This type of transition is similar to
the transitions that occur in ferromagnetic systems
[49].

 , minimal
displacement is easily achieved.
, minimal
displacement is easily achieved.
 ) is very flat
and has minimal curvature. In terms of (63) and
(64) this suggests that inflation will occur as long as
the SRA requirements hold.
) is very flat
and has minimal curvature. In terms of (63) and
(64) this suggests that inflation will occur as long as
the SRA requirements hold.


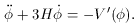
 2 and
2 and
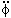 terms. This
leaves the more tractable equations shown below, which remain
valid until
terms. This
leaves the more tractable equations shown below, which remain
valid until  approaches the true
vacuum; i.e.,
approaches the true
vacuum; i.e.,  ~ 1.
~ 1.
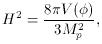

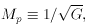
 = c = 1.
= c = 1.
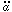 > 0.
First note that
> 0.
First note that
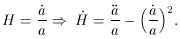
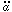 (t) > 0 and a(t) is
always positive thus,
(t) > 0 and a(t) is
always positive thus,
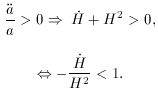

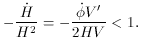
 and
plugging the result into the last equation, we obtain
and
plugging the result into the last equation, we obtain
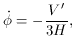

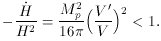
 << 1. So
again one is reminded that inflation will take place until
<< 1. So
again one is reminded that inflation will take place until
 ~ 1, which has been shown
to be equivalent to
~ 1, which has been shown
to be equivalent to  > 0.
> 0.
26 The
Planck mass is easier to work with opposed to Newton's constant
G, since most of the interesting energy scales are on the order
of GeV (1 eV = 1.6 x 10-19 Joules). In these
units, the Planck mass is  1019 GeV. Back.
1019 GeV. Back.