


2. The Amount of Inflation
One can find the amount of inflation by considering the change of the scale factor. Considering the example of quasi-exponential expansion, meaning that the Hubble constant need not be constant. Then,
Using the slow-roll equations, the number of e-foldings can be
expressed in terms of the inflaton potential. Dividing
(73) by (72) yields,
Using this result, with the formula for N
(76), one gets,
Here the fact that the SRA has been used is expressed
using `
For N > 60, which is needed to solve the initial value
problems [22],
we again find
Given the slow-roll conditions and the number of required
e-foldings (N), one can test a model inflaton to see
if it is compatible with an inflationary scenario. With this
generic framework that has been set forth, one can construct
particle theories and then test their validity within the context
of inflation theory. However, the slow-roll approximation and
initial value problems (N > 60) are not the only
constraints on the inflaton and therefore particle theory. The
inflaton is further restricted by the predicted large-scale
structure of the universe, along with the mechanisms involved with
reheating of the universe at the end of inflation. The large-scale
structure is determined by density perturbations resulting from
quantum fluctuations in the evolution of the inflaton field. This
analysis can actually be done without the advent of quantum
gravity; however, it is outside the scope of this paper. Instead,
the author hopes to manifest the stringency of these parameters on
the inflaton field by addressing the observational consequences
and predictions that inflation offers. In the next section these
observational tests will be explored.
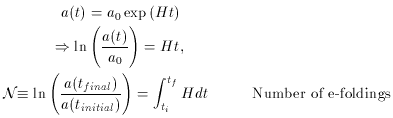
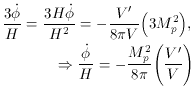
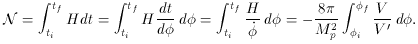
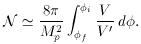
 ' in (78).
' in (78).
 >>
Mp. This
can be seen from (78), where V' ~ V /
>>
Mp. This
can be seen from (78), where V' ~ V /
 using the SRA. This means that if one chooses a potential of
1/2 m2
using the SRA. This means that if one chooses a potential of
1/2 m2
 2, one must choose the
coupling, m2
to be small. Given a self interacting potential term,
2, one must choose the
coupling, m2
to be small. Given a self interacting potential term,

 4, the coupling must be
extremely weak,
4, the coupling must be
extremely weak,
 << 1.
This coupling agrees nicely with theories of supergravity and
certain string theories, although other potentials are ruled out
because of their couplings, such as the weak coupling. This
leaves the question. Can inflation be considered without a theory
of quantum gravity? As mentioned before, the inflationist is often
not concerned with these initial stages of inflation. The common
standpoint is that chaotic inflation can present an evolution and
then one studies the predictions of this evolution. As
aesthetically displeasing as this may be, it allows cosmology to
progress further without a quantum theory of gravity. Ultimately
this issue will be addressed to create a complete picture of the
creation of the universe; however, Guth has recently shown this
consideration may not need to be considered
[44],
[43].
<< 1.
This coupling agrees nicely with theories of supergravity and
certain string theories, although other potentials are ruled out
because of their couplings, such as the weak coupling. This
leaves the question. Can inflation be considered without a theory
of quantum gravity? As mentioned before, the inflationist is often
not concerned with these initial stages of inflation. The common
standpoint is that chaotic inflation can present an evolution and
then one studies the predictions of this evolution. As
aesthetically displeasing as this may be, it allows cosmology to
progress further without a quantum theory of gravity. Ultimately
this issue will be addressed to create a complete picture of the
creation of the universe; however, Guth has recently shown this
consideration may not need to be considered
[44],
[43].