


1. Modeling the Inflaton Field
The equations of motion derived above (72), (73)
describe the evolution of an arbitrary potential
V( ) subject
only to the constraint that V(
) subject
only to the constraint that V( )
conform to the slow roll
conditions away from its minimum. As mentioned previously, the
conditions for inflation are arbitrary and inflation will occur as
long as
)
conform to the slow roll
conditions away from its minimum. As mentioned previously, the
conditions for inflation are arbitrary and inflation will occur as
long as 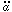 > 0. There are three
cases that are of particular
interest [22].
> 0. There are three
cases that are of particular
interest [22].
 )
)

 n. This
gives a scale factor which behaves quasi-exponentially.
n. This
gives a scale factor which behaves quasi-exponentially.
For particle theorist n = 2, 4 are most favorable, since they
describe renormalizable particle theories
[41].
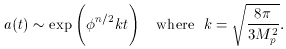
 ) ~ exp (-sqrt[(16
) ~ exp (-sqrt[(16
 / n)]
/ n)]
 / Mp). This
gives a(t) ~ tn. The only
requirement being that n > 1.
/ Mp). This
gives a(t) ~ tn. The only
requirement being that n > 1.
 ) ~
) ~
 F, where
F = 4(n-1 - 1). This yields a(t) ~
e(t/t0)n.
F, where
F = 4(n-1 - 1). This yields a(t) ~
e(t/t0)n.
As an example consider a simple polynomial model with n = 2.
The slow roll condition
In other words, the inflaton field must be larger than the Planck
energy. This is actually the value one would expect for the
cosmological constant, since the only natural scale at high energy
is the Planck scale. However, inflation (as it has been
presented) relies on the evolution of a classical field. If the
value of the field is in the quantum regime, where the Planck
scale lives, inflation can not be treated classically.
Fortunately, there are many resolutions to this problem. First,
what really matters in the field equations is the potential energy
density of the field; namely,
Remember that V appeared
in the Lagrangian density, thus V is actually a density. From
this equation one can see that the magnitude of the potential,
and, therefore, the energy scale of the theory, depend on `m' as
well as
Another resolution to this scale problem is to limit
considerations to the final part of the evolution of the inflaton.
As stated before, the inflaton evolves until
one e-folding is defined as the amount of time for a to grow by
a factor of e:
It will be shown that only
60 e-foldings are needed to resolve the initial value problems and
the scales that are important in determining structure in the
universe only depend on modes that are present during these last
60 e-foldings.
However, it must be pointed out that many people find problems
with these conditions on 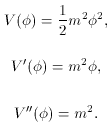
 <
1 impllies
<
1 impllies
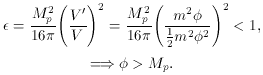
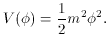
 . `m' represents the
mass of the inflaton and one resolution to the high value of
. `m' represents the
mass of the inflaton and one resolution to the high value of
 is to introduce a small
mass for the inflaton; i.e., make `m' small.
is to introduce a small
mass for the inflaton; i.e., make `m' small.
 = 1 when the
inflaton then reheats the universe. The most important
consequences of inflation are its resolution of the initial value
problems and its predictions about large-scale structure and the
cosmic background anisotropies. As we will see most of these
phenomena only require analysis of the last moments of
`e-foldings' of inflation. E-folding is a way of measuring how
the scale factor increases. Since,
= 1 when the
inflaton then reheats the universe. The most important
consequences of inflation are its resolution of the initial value
problems and its predictions about large-scale structure and the
cosmic background anisotropies. As we will see most of these
phenomena only require analysis of the last moments of
`e-foldings' of inflation. E-folding is a way of measuring how
the scale factor increases. Since,
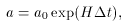
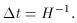
 . The idea
of fine-tuning the mass
of the inflaton `m' is certainly unappealing. One of the
appealing aspects of inflation was its resolution of the initial
value or fine-tuning problems of the Big Bang model. But, now we
are again confronted with an initial value problem. This problem
can be resolved by addressing inflation in the context of a
quantum gravity theory such as superstring theory. I will not
pursue such issues in this paper, although the reader is again
referred to the eprint archive for recent
efforts (27)
. The idea
of fine-tuning the mass
of the inflaton `m' is certainly unappealing. One of the
appealing aspects of inflation was its resolution of the initial
value or fine-tuning problems of the Big Bang model. But, now we
are again confronted with an initial value problem. This problem
can be resolved by addressing inflation in the context of a
quantum gravity theory such as superstring theory. I will not
pursue such issues in this paper, although the reader is again
referred to the eprint archive for recent
efforts (27)