


A. Perturbations and Large-Scale Structure
During the inflation epoch, perturbations (small fluctuations) of two types are generated: scalar (density) perturbations, and tensor (metric) perturbations. The scalar perturbations come from quantum fluctuations of the inflaton field before and during its evolution. Tensor perturbations arise from quantum fluctuations in the space-time metric within the quasi-DeSitter spacetime. Fluctuations of this type are a natural consequence of a DeSitter spacetime.
In DeSitter space there exists an event horizon. Consider the distance light can travel in comoving coordinates, which is given by (6) and a(t) ~ exp(Ht).
The presence of this event horizon suggests the
presence of thermal fluctuations in the fields, similar to those
present in a black hole. This can be understood by appealing to
the uncertainty principle. The event horizon causes the ground
state modes of any fields present to be restricted in spatial
extent. The uncertainty principle then requires,
where k is the Boltzman constant relating the
energy to the temperature.
This result provides a motivation for the existence of
fluctuations in the metric and scalar field. As these
perturbations are created during inflation they are inflated
outside of the causal horizon (particle horizon). As mentioned in
the previous section, the causal horizon is nearly stationary
during inflation. Once the perturbation has been inflated outside
the horizon, its ends are no longer in causal contact. In this
way, the perturbations become `frozen-in' as classical
perturbations.
Ignoring the nonlinear, or super-horizon, effects of these
perturbations may trouble the reader. However, as we shall see,
ignoring these effects appears to be in agreement with the cosmic
background data
[57],
[58],
[59].
As stated,
one reason for choosing to ignore super-horizon evolution is the
causal separation of the ends of the perturbation. However, this
argument is far from rigorous and the study of nonlinear
perturbations takes much care. Perturbation evolution relies on
the extrinsic (super-horizon) properties of the spacetime manifold
and is sensitive to the gauge of general relativity. The
perturbation evolution can usually be ignored in regions where the
pressure becomes negligible, which happens to be on the order of
the horizon [22].
This generally motivates one to
ignore the super-horizon evolution, however for a complete
treatment, see
[60],
[61],
[5,
Chapter 8 and
9].
After inflation the expansion continues at sub-luminal speeds and
these perturbations enter back inside the causal horizon. Thus,
the most important perturbations for creating structure come from
the ones that were exited near the end of the inflationary period
(i.e., approximately the last 60 e-foldings). After the reheating
process occurs, the inhomogeneities passing back inside the
horizon cause fluctuations that seed the large-scale structure.
Pure exponential inflation, which corresponds to a DeSitter
spacetime, has an interesting property. The spacetime is invariant
under time translation. That is to say, there is no natural origin
of time under true exponential expansion
[22,
Chapter 11]. The only fundamental size in the theory is that of
the Hubble horizon (c/H). Thus, one expects that the amplitude
of a `standing wave' perturbation will be related to the horizon
size, c/H, which is not changing. Therefore, we see why
inflation predicts a scale-invariant spectrum for the
perturbations.
This analysis can be illustrated through musical analogy. The
fundamental mode of the perturbations are determined by the Hubble
distance (c/H), much like the fundamental mode of a flute is
determined by its length. Because the Hubble length (horizon) is
nearly stationary during inflation, this means inflation
predicts a scale-invariant, or Harrison-Zeldovich spectrum.
Furthering this analogy, the `overtones` of the universe
correspond to the inflaton potential that determines its behavior,
much like overtones can be used to distinguish one instrument from
another. However, as we have seen that inflation need not be
exponential. The small deviations from DeSitter spacetime result
in small deviations from a scale-invariant spectrum. These
deviations can be used to successfully predict the correct
potential for the inflaton.
The generated perturbations can be characterized by a power
spectrum,
where
One is generally interested in the scale dependence of the
spectral index of these perturbations, since this dependence
changes for different inflation models
[62].
For an absolute scale-invariant spectrum, it follows that
The details of the calculation need not concern us here,
for a derivation of this result see
[15] or
[22].
This relation is only presented to demonstrate
that the tilt, which is a discriminating factor between models,
can be written in terms of the SRA parameters
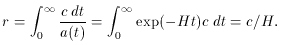
 p
p

 H/c, since the
characteristic size is just c/H.
This uncertainty in momentum gives rise to energy fluctuations and
the corresponding Hawking temperature is given by
[22],
H/c, since the
characteristic size is just c/H.
This uncertainty in momentum gives rise to energy fluctuations and
the corresponding Hawking temperature is given by
[22],

 H2(k).
The H indicates that the
perturbation amplitude is taken to correspond to its value when it
crossed the causal horizon. Quantitatively, this corresponds to
k = aH, where k is the wave number of the
perturbation. Quantum
field theory can be used to calculate an expression for
H2(k).
The H indicates that the
perturbation amplitude is taken to correspond to its value when it
crossed the causal horizon. Quantitatively, this corresponds to
k = aH, where k is the wave number of the
perturbation. Quantum
field theory can be used to calculate an expression for
 H similar to
Equation (80) above
[22,
Chapter 8].
H similar to
Equation (80) above
[22,
Chapter 8].
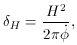
 is the inflaton. This
formula manifests
the connection between the inflaton potential and the
perturbations generated during inflation.
is the inflaton. This
formula manifests
the connection between the inflaton potential and the
perturbations generated during inflation.
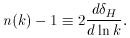
 is independent of k and the above relation gives n = 1 as one
would expect. For a spectrum that is nearly scale-invariant the
amount n differs from one is referred to as the tilt of the
spectrum. Although it is not at all obvious, (81) and
(82) can be used along with the slow roll parameters
(64), (63) to express the tilt as,
is independent of k and the above relation gives n = 1 as one
would expect. For a spectrum that is nearly scale-invariant the
amount n differs from one is referred to as the tilt of the
spectrum. Although it is not at all obvious, (81) and
(82) can be used along with the slow roll parameters
(64), (63) to express the tilt as,
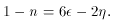
 and
and
 . Therefore, if an
experimental consequence of the tilt is
observable, one can find the appropriate values for the SRA and
reconstruct the inflaton potential
[63].
. Therefore, if an
experimental consequence of the tilt is
observable, one can find the appropriate values for the SRA and
reconstruct the inflaton potential
[63].