


B. The Cosmic Background Anisotropies
The discovery of the anisotropies in the cosmic background by COBE created a new opportunity for verification of cosmological parameters and theories of large-scale formation. As discussed at the beginning of this paper, the CMB offers a `snap-shot' of the universe at the time of recombination (z ~ 1000). The anisotropies that were present in the baryon-photon plasma at this time are manifested today by the temperature fluctuations in the spectrum. These fluctuations are representative of a nearly Gaussian, scale-invariant spectrum. As discussed previously, this is a unique prediction of inflation theories.
Although the quantitative details can become formible, the qualitative description of these temperature fluctuations is quite simple. During inflation, the perturbations formed must be of nearly the same amplitude and randomly distributed, as discussed above. After reheating takes place, these classical perturbations re-enter the horizon causing density fluctuations in the baryon-photon plasma. In over-dense regions, potential wells form that trap the plasma and cause it to heat up. At the same time, photon pressure induces a kind of restoring force to oppose the gravitational potential. In this way, a harmonic oscillator motion is set up in the plasma. These oscillations continue with no friction (viscosity) from the fluid. This is why they are referred to as adiabatic fluctuations. However, if this were not the case and the friction is deemed important, one obtains an isocurvature spectrum [64]. These turn out to be indicative of cosmic strings, which are ruled-out by observation as a method of primordial structure formation. However, models containing cosmic strings that are produced during reheating following inflation may still play a major role in cosmological models [65].
At the time of recombination, when the photons were able to escape the fluid, they had to overcome the gravitational potentials. The picture is that the photons in these potential wells were hotter than the average, but this temperature difference was partially cancelled by the gravitational redshift resulting from the photons `climbing' out of the potential well. This phenomena is know as the Sachs-Wolf effect. The result is that the photons that were in the wells have a slight temperature increase from those that were not. This variation is predicted by theory to be on the order of 10-5 [22]. These oscillations propagate through the fluid at the speed of sound. Thus, there is a acoustic horizon that is generated within the surface of last scattering and if present today would have an angular size of about one degree on the sky.
One concern with the simplicity of this analysis is what effects, such as reionization in the surface of last scattering, must be considered? It is important to consider the mean free path of the photon as it travels within the fluid before escaping. This could affect the energy and therefore temperature of the spectrum. However, it turns out that this effect only appears on small angular scales within the spectrum and can be ignored [58]. Also, any effects from CMB scattering off interstellar gas only appear in the spectrum at very small angles. These observations are of course useful, but offer little insight into examination of the early universe and formation of large-scale structure.
Given the predicted anisotropies from the Sachs-Wolf effect, the next step is to examine the cosmic background spectrum through observation. The anisotropies in the temperature of the cosmic background spectrum can be expanded in spherical harmonics [56],
The multipole coefficients are given by,
The amount of anisotropy at multipole moment l is
expressed by the power spectrum,
The Cl's measure the temperature anisotropy of two regions
separated by angle
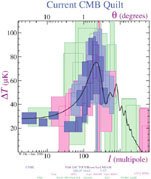
When the COBE data is plotted with multipole l versus
temperature variation, a peak is found to occur around l = 220 or
1° (Figure (10)). This peak corresponds to the
angular size on the sky of the acoustic horizon discussed before
and has been called the Doppler peak. Thus, there is a maximum
temperature variation at precisely the angle predicted by the
Sachs-Wolf effect. Since a mechanism of this type can only be
explained by an inflationary model, one is presented with a strong
argument for inflation
[64].
Figure 10. Power Spectrum Plot of the
Cosmic Background - The data
is normalized to the quadrupole (l = 2) anisotropy detected by
COBE. The Doppler peak corresponds to a maximum power fluctuation
at a multipole of l = 220, which is about an angle of one degree
on the sky. This graph provided by Wayne Hu
[64].
However, the peak is actually sensitive to the cosmological
parameters, such as the Hubble constant and the curvature of the
universe. If the universe is non-flat then the null geodesics are
found to converge (diverge) in the case of spherical (hyperbolic)
geometry. The angle subtended is given by
The cosmic background is apparently richer in structure than was
first realized. As we have discussed, inflation predicts
fluctuations in both the scalar and tensor fields. This gives
rise to slight differences in the anisotropies at small angles
(large l). Also, there are multiple peaks in the spectrum
following the peak at l = 220 and the height and shape of the
spectrum are related to the specifics of inflation models, such as
the tilt.
To examine one aspect of the complexity involved, consider that
the scalar and tensor perturbations can be fixed by their
contribution to the quadrupole moment Cl=2 of the CMB
[66].
where V = V(
Although most models of inflation predict a near scale-invariant,
or Harrison-Zel'dovich spectrum, the small deviations from
differing potentials V(
However, the ultimate test of inflation is the precise
determination of the tensor perturbations, that is the nt's.
This can't be deduced from the CMB spectrum because both the
scalar and tensor perturbations contribute to the temperature
anisotropy. However, if a method could be devised to separate out
the tensor perturbations and this spectrum were detected, it would
be concrete evidence of an inflationary period. This is because
inflation is the only way metric perturbations can survive to the
present. This is due to the structure of a DeSitter spacetime.
The tensor spectrum can be separated by creating a polarization
map of the CMB. The separation is then possible because the
tensor perturbations have an intrinsic axial component, and the
angular dependence can be determined from the metric. Whereas, the
scalar perturbations have no dependence on direction. Therefore,
the polarization vector can be constructed out of two parts, a
curl and a gradient.
where
The polarization tensor can be expanded in tensor spherical
harmonics [70],
The YG(lm)ab and
YC(lm)ab represent a basis for
the gradient (scalar) and curl (tensor) perturbation terms in this
polarization mapping. The aG(lm)'s and
aC(lm)'s
are again just found by exploiting the orthogonality. One can use
this spectrum to construct necessary requirements for the
potentials of the inflaton field and this analysis can therefore
be used to distinguish the various inflation models.
28 http://map.gsfc.nasa.gov. Back.
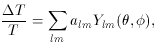
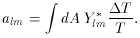
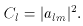
 . This angle
is related to the l's
by:
. This angle
is related to the l's
by:  ~ 180° /
l. Thus, l allows one to express
the temperature variations of regions separated by an angle
180° / l. The l = 0 represents the monopole contribution to
the anisotropy, which is of course zero (this is comparing a point
separated from itself by 360°. The next moment, l = 1, is
the dipole moment, which compares regions separated by
180°. This anisotropy originates from our peculiar
velocity, the motion of the Earth relative to the cosmic
background. This moment is usually taken out of the spectrum to
leave the `true' anisotropy. The l = 2 moment is the quadrupole
contribution, which marks the first non-trivial anisotropy for
understanding structure formation.
~ 180° /
l. Thus, l allows one to express
the temperature variations of regions separated by an angle
180° / l. The l = 0 represents the monopole contribution to
the anisotropy, which is of course zero (this is comparing a point
separated from itself by 360°. The next moment, l = 1, is
the dipole moment, which compares regions separated by
180°. This anisotropy originates from our peculiar
velocity, the motion of the Earth relative to the cosmic
background. This moment is usually taken out of the spectrum to
leave the `true' anisotropy. The l = 2 moment is the quadrupole
contribution, which marks the first non-trivial anisotropy for
understanding structure formation.
 H ~
H ~
 1/2 1°. This
means for the peak at l = 220 we
live in a universe which is flat. Although, this seems to
represent a bit of circular logic. This difficulty can be
remedied by calling upon other observational tests to constrain
the parameters. These includ galaxy surveys, lensing experiments,
or standard candle observations. When all of these methods are
combined, strong constraints can be put on parameters and the best
model can be determined.
1/2 1°. This
means for the peak at l = 220 we
live in a universe which is flat. Although, this seems to
represent a bit of circular logic. This difficulty can be
remedied by calling upon other observational tests to constrain
the parameters. These includ galaxy surveys, lensing experiments,
or standard candle observations. When all of these methods are
combined, strong constraints can be put on parameters and the best
model can be determined.
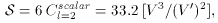
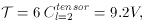
 ) is the
inflaton potential, S is the
scalar contribution, and T is the tensor contribution.
When the slow-roll approximation is considered and the
determination of cosmological parameters is found by methods other
than CMB analysis; e.g., for large-scale structure probing, one
finds that the ratio T/S is less than order unity.
This restricts V
) is the
inflaton potential, S is the
scalar contribution, and T is the tensor contribution.
When the slow-roll approximation is considered and the
determination of cosmological parameters is found by methods other
than CMB analysis; e.g., for large-scale structure probing, one
finds that the ratio T/S is less than order unity.
This restricts V  5 x
10-12. Reformulating equation
(82) in terms of the inflaton potential, one finds in
Planckian units the relations for the scalar and tensor spectral
indices, respectively.
5 x
10-12. Reformulating equation
(82) in terms of the inflaton potential, one finds in
Planckian units the relations for the scalar and tensor spectral
indices, respectively.
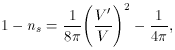
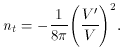
 )
give a way of testing inflation
models. With future experiments such as
MAP (28)
and
PLANCK (29) ,
these spectral indices will be found with great precision and the
shape and height of the spectrum can be used to manifest the
correct inflaton potential. In this way, inflation will be used to
predict new particle physics, instead of the original scenario
which was vice versa.
)
give a way of testing inflation
models. With future experiments such as
MAP (28)
and
PLANCK (29) ,
these spectral indices will be found with great precision and the
shape and height of the spectrum can be used to manifest the
correct inflaton potential. In this way, inflation will be used to
predict new particle physics, instead of the original scenario
which was vice versa.
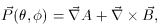
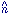 gives the direction. Thus,
to obtain the tensor terms
one can take the divergence of this vector. Before proceeding
further, it may be of interest to the reader why the perturbations
only contain tensor and scalar contributions and vector type
perturbations are absent. This is because massless vector fields
are conformally invariant
[67].
This invariance can
be broken by introducing a mass term or by explicitly breaking the
coupling. Although for a massive vector field the perturbations
generated are far too small and die off far too quickly during the
inflationary expansion
[68].
Thus, a standard
prediction of inflation is that there are no vector perturbations.
But, isn't the polarization a vector? No. The polarization is
actually a 2 x 2 trace free symmetric tensor. This tensor
is written in terms of the Stokes parameters
Q(
gives the direction. Thus,
to obtain the tensor terms
one can take the divergence of this vector. Before proceeding
further, it may be of interest to the reader why the perturbations
only contain tensor and scalar contributions and vector type
perturbations are absent. This is because massless vector fields
are conformally invariant
[67].
This invariance can
be broken by introducing a mass term or by explicitly breaking the
coupling. Although for a massive vector field the perturbations
generated are far too small and die off far too quickly during the
inflationary expansion
[68].
Thus, a standard
prediction of inflation is that there are no vector perturbations.
But, isn't the polarization a vector? No. The polarization is
actually a 2 x 2 trace free symmetric tensor. This tensor
is written in terms of the Stokes parameters
Q(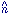 ) and
U(
) and
U(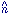 ), which give us the
polarization in each direction.
For an explanation of these parameters see,
[69,
section 7.2].
), which give us the
polarization in each direction.
For an explanation of these parameters see,
[69,
section 7.2].

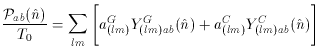
29 http://astro.estec.esa.nl/SA-general/Projects/Planck.
Back.