


 AND FUNDAMENTAL PLANE RELATIONS FOR ELLIPTICAL GALAXIES
AND FUNDAMENTAL PLANE RELATIONS FOR ELLIPTICAL GALAXIES
If the TF relation has been the workhorse of modern
velocity field studies, the Dn- relation has
been a short step behind. The closest analogue to
the TF relation for elliptical galaxies is actually
the predecessor of Dn-
relation has
been a short step behind. The closest analogue to
the TF relation for elliptical galaxies is actually
the predecessor of Dn- , the Faber-Jackson (FJ) relation.
FJ expresses the power-law correlation between an elliptical
galaxy's luminosity and its internal velocity dispersion,
, the Faber-Jackson (FJ) relation.
FJ expresses the power-law correlation between an elliptical
galaxy's luminosity and its internal velocity dispersion,
where the exponent
These surveys bore unexpected fruit, however, in the latter
part of the 1980s. Two groups conducting
surveys of ellipticals arrived independently at a new
result: the FJ correlation could be considerably tightened
by the addition of a third parameter, namely, surface brightness
(Djorgovski & Davis
1987;
Dressler et al. 1987).
In its modern incarnation, the new correlation has become
known as the Dn-
where
More broadly, Dn-
An early determination of the parameters
The two-dimensionality of the loci in parameter
space occupied by ellipticals
actually makes the FP relations, including Dn-
with
The discovery of the fundamental plane relations was crucial
to the use of ellipticals in peculiar velocity surveys because of their
much increased accuracy over Faber-Jackson. For example,
Jorgensen et
al. (1996)
estimate that
the scatter in log (Re) at fixed
The Dn-
Like the TF relation, the FP relations are now being studied
at appreciable redshift as well. Recently,
Bender et al. (1996)
have studied a sample of cluster ellipticals at z = 0.37. They
have found evidence for mild (~ 0.5 mag) evolution
toward brighter magnitudes at such redshifts, comparable to
the result found by
Vogt et al. (1996)
for the TF relation.
Because it is difficult to find Cepheids in nearby elliptical
galaxies, there has been little attempt to provide
absolute calibrations of the Dn-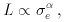
 was found
empirically to be ~ 4 ± 1
(Faber & Jackson 1976;
Schechter 1980;
Tonry & Davis 1981).
Although discovered around the
same time, and viewed as closely related in physical origin,
TF and FJ were not considered equivalently good distance
indicators. It was clear from the outset that the scatter
in the FJ relation was about twice that of the TF relation,
on the order of 0.8 mag. Thus, while the TF relation flourished
in the early 1980s as a tool of distance measurement
(Section 3),
elliptical galaxy surveys focused more on
the stuctural and dynamical implications of the FJ relation.
was found
empirically to be ~ 4 ± 1
(Faber & Jackson 1976;
Schechter 1980;
Tonry & Davis 1981).
Although discovered around the
same time, and viewed as closely related in physical origin,
TF and FJ were not considered equivalently good distance
indicators. It was clear from the outset that the scatter
in the FJ relation was about twice that of the TF relation,
on the order of 0.8 mag. Thus, while the TF relation flourished
in the early 1980s as a tool of distance measurement
(Section 3),
elliptical galaxy surveys focused more on
the stuctural and dynamical implications of the FJ relation.
 relation: a power-law correlation
between the luminous diameter
Dn-
relation: a power-law correlation
between the luminous diameter
Dn- and the
internal velocity dispersion
and the
internal velocity dispersion  ,
,
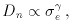
 = 1.20 ± 0.10
(Lynden-Bell et
al. 1988).
(Dn-
= 1.20 ± 0.10
(Lynden-Bell et
al. 1988).
(Dn- is
defined as the diameter within which the galaxy has a given
mean surface brightness. As such, it implicitly incorporates the third
parameter into the correlation.)
is
defined as the diameter within which the galaxy has a given
mean surface brightness. As such, it implicitly incorporates the third
parameter into the correlation.)
 and its variants may be viewed
as manifestations of the Fundamental Plane (FP) of Elliptical
Galaxies, a planar region in the three-dimensional space
of structural parameters
in which normal ellipticals are found.
One expression of the FP relates effective diameter
to internal velocity dispersion and central
surface brightness,
and its variants may be viewed
as manifestations of the Fundamental Plane (FP) of Elliptical
Galaxies, a planar region in the three-dimensional space
of structural parameters
in which normal ellipticals are found.
One expression of the FP relates effective diameter
to internal velocity dispersion and central
surface brightness,
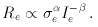
 and
and  using
B-band photometry gave
using
B-band photometry gave

 1.4,
1.4, 
 0.9
(Faber et al. 1987).
More recently,
Bender et al. (1992)
found
0.9
(Faber et al. 1987).
More recently,
Bender et al. (1992)
found  = 1.4,
= 1.4,  = 0.85
using B-band data for a sample of Virgo and Coma cluster ellipticals;
the upper panel of Figure 4
shows the FP for this sample.
A recent R-band FP analysis by
the EFAR group
(Wegner et al. 1996)
is
= 0.85
using B-band data for a sample of Virgo and Coma cluster ellipticals;
the upper panel of Figure 4
shows the FP for this sample.
A recent R-band FP analysis by
the EFAR group
(Wegner et al. 1996)
is  = 1.23,
= 1.23,  = 0.72.
A measurement based on Gunn R-band photometry
(Jorgensen et
al. 1996)
yields a similar value of
= 0.72.
A measurement based on Gunn R-band photometry
(Jorgensen et
al. 1996)
yields a similar value of  (1.24 ± 0.07) but a somewhat
different value of
(1.24 ± 0.07) but a somewhat
different value of  (0.82 ± 0.02), perhaps due to the slightly different bandpass used.
Pahre et al. (1995)
have recently
carried out the first analysis of the FP using K-band
photometry, finding
(0.82 ± 0.02), perhaps due to the slightly different bandpass used.
Pahre et al. (1995)
have recently
carried out the first analysis of the FP using K-band
photometry, finding  = 1.44 ±
0.04,
= 1.44 ±
0.04,  = 0.79
± 0.04.
= 0.79
± 0.04.
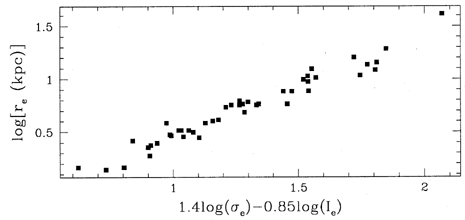
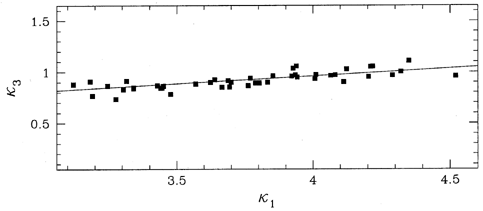
Figure 4. Two versions of the Fundamental Plane for the
Virgo
and Coma ellipticals studied by
Bender et al. (1992).
Further details are given in the main text. (The data used for
these figures were kindly provided by D. Burstein.)
 , somewhat
less mysterious than the one-dimensional TF sequence. As noted
by Faber et
al. (1987),
such two-dimensionality is expected on
virial equlibrium grounds alone. Unlike the TF relation, therefore,
the FP is not obviously related to the relative distribution of
luminous and dark matter.
If the virial theorem were truly all there
was to the FP, however, one would find
re
, somewhat
less mysterious than the one-dimensional TF sequence. As noted
by Faber et
al. (1987),
such two-dimensionality is expected on
virial equlibrium grounds alone. Unlike the TF relation, therefore,
the FP is not obviously related to the relative distribution of
luminous and dark matter.
If the virial theorem were truly all there
was to the FP, however, one would find
re 
 e2
Ie-1. The fact that
the FP coefficients differ significantly from these
values implies that the mass-to-light (M / L) ratios
of ellipticals vary slowly as a function of mass. In particular,
the observed FP relations indicate that
e2
Ie-1. The fact that
the FP coefficients differ significantly from these
values implies that the mass-to-light (M / L) ratios
of ellipticals vary slowly as a function of mass. In particular,
the observed FP relations indicate that
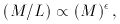

 0.15-0.20.
Bender et al. (1992)
have used this fact to look at the FP in a different way. They
define coordinates (
0.15-0.20.
Bender et al. (1992)
have used this fact to look at the FP in a different way. They
define coordinates ( 1,
1,  2,
2,  3), each of which is
a normalized linear combination of log(
3), each of which is
a normalized linear combination of log( e), log (re),
and log (Ie). The definitions are such that
e), log (re),
and log (Ie). The definitions are such that  1 is
proportional to log (M) and
1 is
proportional to log (M) and  3 is proportional to log
(M/L).
A plot of
3 is proportional to log
(M/L).
A plot of  3 versus
3 versus
 1, shown in the
bottom panel
of Figure 4, is very nearly an edge-on projection
of the FP. The line drawn through the data is
1, shown in the
bottom panel
of Figure 4, is very nearly an edge-on projection
of the FP. The line drawn through the data is  3 = 0.15
3 = 0.15 1 +0.36.
A
1 +0.36.
A  -space analysis of the properties
of elliptical galaxies may provide greater insight into the physical processes
that shaped them
(Bender et al. 1993).
-space analysis of the properties
of elliptical galaxies may provide greater insight into the physical processes
that shaped them
(Bender et al. 1993).
 e and Ie
is 0.084 dex. This corresponds to a distance error of
just over 19%, quite comparable to recent estimates
of the TF distance error (Section 3). Moreover,
Jorgensen et al. have found that the distance error
is reduced to 17% when galaxies with
e and Ie
is 0.084 dex. This corresponds to a distance error of
just over 19%, quite comparable to recent estimates
of the TF distance error (Section 3). Moreover,
Jorgensen et al. have found that the distance error
is reduced to 17% when galaxies with  e < 100 km s-1
are excluded. This effect is reminiscent of the increased
TF scatter at lower velocity widths discussed in
Section 3,
and may arise for the same reason.
Pahre et al. (1995)
find a distance error of 16.5% from the K-band FP.
e < 100 km s-1
are excluded. This effect is reminiscent of the increased
TF scatter at lower velocity widths discussed in
Section 3,
and may arise for the same reason.
Pahre et al. (1995)
find a distance error of 16.5% from the K-band FP.
 relation occupies a special place in the history
of peculiar velocity surveys because it was used in the first
detection of very large-scale streaming by the ``7-Samurai'' group
(Dressler et al. 1987;
Lynden-Bell et
al. 1988).
In the 7-Samurai survey, a full-sky sample of elliptical galaxies
revealed a streaming motion of amplitude ~ 500 km s-1 that was
coherent across the entire sky to a depth of ~ 40 Mpc. Subsequent
studies of spiral galaxies
(Willick 1990;
Han & Mould 1992;
Mathewson et al. 1992;
Courteau et al. 1993)
have lent confirmation
to this result, although the coherence length of the flow remains
controversial. Since the late 1980s no new results concerning
the peculiar velocity field have been obtained using elliptical
galaxy data. However, this situation will change in the coming
years as several large surveys of elliptical galaxies (e.g.,
Wegner et al. 1996)
come to fruition.
relation occupies a special place in the history
of peculiar velocity surveys because it was used in the first
detection of very large-scale streaming by the ``7-Samurai'' group
(Dressler et al. 1987;
Lynden-Bell et
al. 1988).
In the 7-Samurai survey, a full-sky sample of elliptical galaxies
revealed a streaming motion of amplitude ~ 500 km s-1 that was
coherent across the entire sky to a depth of ~ 40 Mpc. Subsequent
studies of spiral galaxies
(Willick 1990;
Han & Mould 1992;
Mathewson et al. 1992;
Courteau et al. 1993)
have lent confirmation
to this result, although the coherence length of the flow remains
controversial. Since the late 1980s no new results concerning
the peculiar velocity field have been obtained using elliptical
galaxy data. However, this situation will change in the coming
years as several large surveys of elliptical galaxies (e.g.,
Wegner et al. 1996)
come to fruition.
 and FP relations. As a result,
elliptical galaxy distances have
not figured prominently in the Hubble constant problem.
However, this situation may change in the near future, if Surface
Brightness Fluctuation distances (discussed in the next Section)
can provide an absolute calibration for
the Dn-
and FP relations. As a result,
elliptical galaxy distances have
not figured prominently in the Hubble constant problem.
However, this situation may change in the near future, if Surface
Brightness Fluctuation distances (discussed in the next Section)
can provide an absolute calibration for
the Dn- and
FP relations.
and
FP relations.