


5.1. Calibration of SBF
It may appear from the brief description above that SBF is a purely ``geometrical method,'' like parallax. If this were true, it would free the method from the nagging questions that plague other DIs: are they really universal, or do they depend on galaxy type, age, environment, and so forth? In reality, however, SBF dependent on the stellar populations in the galaxies to which it is applied. Not only does this mean that we need to be cautious with regard to its univerality, but, also, that it is difficult to derive an absolute calibration of SBF from first principles. Like the other DIs considered in this Chapter, absolute distances obtained from the SBF technique are tied to the Cepheid distance scale. If the latter were to change, so would the SBF distances. In particular, estimates of H0 derived from SBF studies (see below) may well require revision as the HST Key Project (Section 2) yields new results.
The stellar population dependence of SBF
arises because the stars which contribute most strongly
to the fluctuations are those that lie at the tip
of the giant branch. Tonry and coworkers parameterize
this effect in terms of ``effective fluctuation magnitudes''
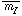 (absolute) and
(absolute) and 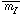 (apparent). The quantity
(apparent). The quantity
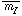 may be thought
of as the absolute magnitude of
the giant branch stars which dominate the fluctuations;
may be thought
of as the absolute magnitude of
the giant branch stars which dominate the fluctuations;
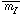 is an apparent
magnitude obtained from the observed fluctuations. If all galaxies had
identical stellar populations, they would all
have the same value of
is an apparent
magnitude obtained from the observed fluctuations. If all galaxies had
identical stellar populations, they would all
have the same value of 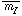 , and their distance
moduli would be given simply by
, and their distance
moduli would be given simply by 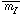 -
- 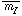 .
.
Because galaxies do not have identical stellar
populations, it is necessary to
determine an empirical correction to 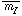 as a function of a distance-independent galaxian
property. Tonry and coworkers use (V - I) color
for this purpose. Their most recent calibration is
as a function of a distance-independent galaxian
property. Tonry and coworkers use (V - I) color
for this purpose. Their most recent calibration is
which is valid for 1.0
The correlation of fluctuation magnitude
with color is quite strong.
Accurate colors are therefore required in order to minimize
systematic effects. The possibility that the slope or zero point of
this correlation may not be universal, but instead
depend on some as yet undetermined galaxy properties as suggested by
Tammann (1992),
merits further attention. However,
Tonry et al. (1997)
show that the most
likely manifestation of such a problem, a trend
with metallicity of residuals from the 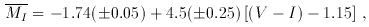
 (V-I)
(V-I)  1.3
(Tonry et al. 1997).
We discuss the zero point of this
relation in Section 5.2.
The color dependence indicated by equation 10
is readily seen in the
1.3
(Tonry et al. 1997).
We discuss the zero point of this
relation in Section 5.2.
The color dependence indicated by equation 10
is readily seen in the  versus
(V - I) diagrams of several tight groups and clusters, as
shown in the upper panel of Figure 5.
A line of slope 4.5 - the solid lines drawn
throught the data points - fits the fluctuation magnitude-color
data in each group well. (The solid points, as well
as the small open squares, are thought to be non-members of the groups.)
The different intercepts of the solid lines reflect the
different distances to the groups.
versus
(V - I) diagrams of several tight groups and clusters, as
shown in the upper panel of Figure 5.
A line of slope 4.5 - the solid lines drawn
throught the data points - fits the fluctuation magnitude-color
data in each group well. (The solid points, as well
as the small open squares, are thought to be non-members of the groups.)
The different intercepts of the solid lines reflect the
different distances to the groups.

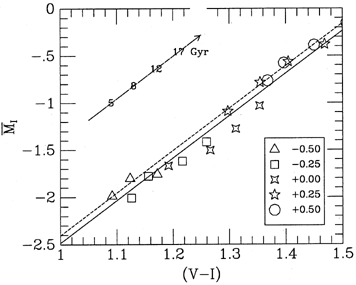
Figure 5. Top panel: fluctuation apparent magnitudes
 versus (V -
I) color for several nearby groups
and clusters. The solid lines drawn through the data points all have
slope 4.5. Bottom panel: a plot of the theoretical
versus (V -
I) color for several nearby groups
and clusters. The solid lines drawn through the data points all have
slope 4.5. Bottom panel: a plot of the theoretical 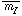 versus
(V - I) relation, from the stellar population synthesis models of
Worthey (1994).
The different point types indicate different
metallicities relative to the Milky Way, as coded in the inset.
For each point type, there are several distinct points,
corresponding to different stellar population ages, as
indicated by the arrow. The solid line
is a fit to the theoretical models with
slope fixed at 4.5. The dashed line is the empirical relation,
equation 10. Adapted from
Tonry et al. (1997).
versus
(V - I) relation, from the stellar population synthesis models of
Worthey (1994).
The different point types indicate different
metallicities relative to the Milky Way, as coded in the inset.
For each point type, there are several distinct points,
corresponding to different stellar population ages, as
indicated by the arrow. The solid line
is a fit to the theoretical models with
slope fixed at 4.5. The dashed line is the empirical relation,
equation 10. Adapted from
Tonry et al. (1997).
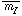 - (V - I)
relation, does not exist. It is reassuring, moreover,
that theoretical stellar population synthesis models
predict a trend of fluctuation magnitude with color
that is very similar to the empirical one.
This is shown in the lower panel of
Figure 5, in which the population synthesis models
of Worthey (1994)
are plotted in the
- (V - I)
relation, does not exist. It is reassuring, moreover,
that theoretical stellar population synthesis models
predict a trend of fluctuation magnitude with color
that is very similar to the empirical one.
This is shown in the lower panel of
Figure 5, in which the population synthesis models
of Worthey (1994)
are plotted in the 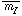 - (V - I)
plane. The points represent models of various metallicities
relative to the Milky Way (indicated by point type as
coded in the inset of the figure), and of various ages
(the trend with age, at a given metallicity, is indicated
by the arrow). The solid line, which has slope 4.5 and
an intercept determined by fitting to the
theoretical models, is seen to be a reasonable fit. The
dashed line is the emprical relation, equation 10. The zero point
of the theoretical relation differs from that of the empirical
one by only 0.07 mag.
- (V - I)
plane. The points represent models of various metallicities
relative to the Milky Way (indicated by point type as
coded in the inset of the figure), and of various ages
(the trend with age, at a given metallicity, is indicated
by the arrow). The solid line, which has slope 4.5 and
an intercept determined by fitting to the
theoretical models, is seen to be a reasonable fit. The
dashed line is the emprical relation, equation 10. The zero point
of the theoretical relation differs from that of the empirical
one by only 0.07 mag.