


We shall not discuss all of the cosmological implications here. The ones that are perhaps the most important are a detailed picture of the spontaneous birth of the Universe and the perturbations that led to the present-day structure (galaxies, clusters, and other density fluctuations). The spontaneous birth of the Universe, the inflationary expansion, and the subsequent evolution of the Universe remain unclear and warrant another review (or rather several reviews). So what follows is two short remarks having a direct bearing on the scalar field theory. The first concerns the hypothesis of an eternally bouncing Universe. Consider a closed Universe whose expansion is limited by some amax greater than 1028 cm (the region that is now observable). In the simplest case, collapse will follow the expansion. At some instant of time (long after 2 x 1010 years, the present age of the Universe), the collapse becomes catastrophic and gives rise to infinite density. Can this collapse be reversed and give birth to a new cycle, similar to that which we now observe? There are several arguments (beginning with Tolman's remark concerning the irreversible growth of entropy) against this picture of the Universe. We shall not repeat these arguments here. But new hope for this arose in connection with the existence of formal symmetric bouncing solutions in scalar field theory. In particular, the Higgs field with
yields a solution
A reasonable Vmax (corresponding to very heavy
X mesons), on the
order of (1014 GeV)4 in
But an analysis of the behavior of the scalar field during compression
and expansion shows that this picture is very improbable.
The argument against periodic repeating cycles of expansion and
collapse is an argument in favor of the spontaneous birth of the
Universe. For a detailed discussion of the spontaneous birth of the
Universe, we refer the reader to the proceedings of the October 1984
Moscow symposium
(Quantum Gravity 1984);
for an earlier attempt,
see
Grishchuk and Zel'dovich
(1982).
Here, we shall only stress that
inflationary expansion is necessary in the overall picture. This is a third
argument, closely related to the two arguments of
Guth (1981)
(horizon and flatness), but not identical.
Assume that the Universe was born with a radius equal to the Planck
radius (10-33 cm) and a density equal to the Planck density
(1093 g cm-3). Then assume that the expansion
proceeds without inflation, like a plasma
(
What is the density we should have at present, when a
These numbers are completely unacceptable - the present density of
the Universe is on the order of 10-30 g cm-3.
This is a crude but weighty argument that shows that an inflationary
phase with constant (or approximately constant) density during very
strong expansion (a factor of ~ 1030) is necessary. This can
be provided by the scalar field, with its peculiar
This is why an astronomer should read this oversimplified story of
the scalar field. The responsibility for the English remains my own.
Thanks to Professors L. P. Grishchuk and L. B. Okun' for
discussions and to L. V. Rozhanskii for assistance.
Let us now return to the astronomer described in the introduction
who works with telescopes but wishes to have a broader understanding.
I do not pretend to give you the ultimate answer - it is not yet known.
But perhaps you now know something about the language highbrow
theoreticians use to talk about the early Universe. But even this modest
goal has only been partially achieved. Alas, the ultimate topic - the
very birth of the Universe - remains out of reach of even the highest
brow.
12 High temperature helps maintain
13 Another variant exists, where the
negative pressure is due to the polarization of the vacuum (see
(Starobinskii 1980)).
This subject is too complicated to
treat here, but we hope to return to it in another review paper.
Back.

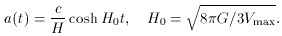
 = c = 1 units,
would lead to an
H0 = 109.GeV =
1035 s-1 and an amin =
c/H0 = 10-25 cm in the usual units.
= c = 1 units,
would lead to an
H0 = 109.GeV =
1035 s-1 and an amin =
c/H0 = 10-25 cm in the usual units.
 = 0, V =
Vmax is the only solution in the compression stage. The
general solution is
= 0, V =
Vmax is the only solution in the compression stage. The
general solution is  2
>> V(
2
>> V( ), p =
+
), p =
+ , which leads
to irreversible
collapse (a(t) = (t0 -
t)1/3), at least in
the classical, homogeneous case.
(12)
, which leads
to irreversible
collapse (a(t) = (t0 -
t)1/3), at least in
the classical, homogeneous case.
(12)
 r
r
 a-4) or
simple dust (
a-4) or
simple dust ( d
d
 a-3).
a-3).
 1028 cm? Simple arithmetic yields
1028 cm? Simple arithmetic yields
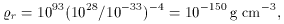
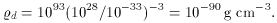

 -
- equation of
state. (13)
equation of
state. (13)
 = 0, V =
Vmax during expansion. But it does not
help prevent collapse during compression.
Back.
= 0, V =
Vmax during expansion. But it does not
help prevent collapse during compression.
Back.