


We shall now write down the basic equations for the radius of the
Universe a(t) and the scalar field
 (t). All other fields
and particles are
neglected. We shall see that this is not just a simplification; it is also a
sound approximation. The equations are
(t). All other fields
and particles are
neglected. We shall see that this is not just a simplification; it is also a
sound approximation. The equations are
and
Equation (8.1) describes the behavior of the field in curved space; in this
case, the curvature is that determined by the expansion. The
characteristic combination
for the various components of Gik that do not vanish
due to the symmetry of the problem
(c
We shall apply the Einstein theory to Friedmann (FRW) universes.
The last term in (8.3), i.e., the k-term - k = - 1 for a
closed universe,
k = 0 for a flat universe, and k = + 1 for a hyperbolic
(open, infinite)
universe - determines their spatial characteristics.
Since the Einstein theory includes the Newtonian theory, one can
give a simple Newtonian interpretation of (8.2) and (8.3). In many
books, it is explained that one can consider a comoving sphere of radius
r(t) =
and the equation of energy conservation
where Em is the kinetic energy per unit mass on the
surface of the sphere
(this specific kinetic energy is conserved). Comparing (8.6) with (8.3) we
obtain
We see that a closed universe corresponds to negative
Em, which
explains why a closed universe collapses again after it expands. A flat
universe corresponds to Em
Comparing them with their parent equations, we see that (8.5) is
obtained from (8.2), so that the corresponding mass,
in contrast to
where V = 4
If the pressure is not equal to zero, the work done by the expanding
sphere, pdv, must be taken into consideration. Let E
denote the total
energy within the sphere, E = Mc2. The first law of
thermodynamics is
It turns out that (8.5) (with M5) and (8.6) (with
M6) and (8.10) (written
for M6) are consistent.
(10) Each of these
three basic equations can be
thought of as resulting from the other two.
The difference between M5 and M6,
and, in particular, the presence
of the 3p term inside the parenthesis in (8.2) is inevitable.
As long as one assumed that the sky was filled with slowly moving
stars, the average pressure could be neglected. The p = 0 equation of
state is called the "dust" equation of state. In the radiation-dominated
phase, p =
The fact that p = -
A particle at a given distance r from the origin is subject to a
positive
acceleration (relative to the origin) if the pressure within the sphere is
large enough and negative. This is not a direct result of the pressure on
the particles because (1) negative pressure is actually tension and (2) it
is the difference in pressure, not the pressure itself, that gives rise to the
accelerative force acting on a particle. Therefore, what (8.2) and (8.5)
describe is the indirect influence of the pressure via the gravitational
field created by the pressure - an effect due to Einstein's general
relativity; this effect is totally unpredicted, even alien to the Newtonian
theory of gravitation.
The gravitational repulsion due to negative pressure is what gives rise
to expansion and the characteristic Hubble velocity distribution.
The first equation governing the evolution of the scalar field (8.1.)
can be deduced from the energy conservation law, which, in turn,
follows from the Einstein equations. Setting dE = -pdV and
E =
If there is only one kind of gravitating substance, then this property
of general relativity turns out to dictate the laws of motion. Along these
lines, before World War II, Einstein and Infeld and Fock and Petrova
independently showed that the laws describing the mechanical motion
of a particle in curved space are a consequence of the geometry of
space - time.
If there is only one field - the scalar field
10 To check this, take the time
derivative of (8.5), accounting for the fact that M is not
constant: dM / dt = -p(dV / dt) = -p .
4
11 The Maxwell equations, which dictate
exact electric charge conservation, have a similar property.
Back.
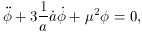
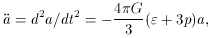
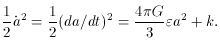
 /
a = (1/a) da/dt = d ln a/dt =
H is the well known Hubble constant. In the general case with
V(
/
a = (1/a) da/dt = d ln a/dt =
H is the well known Hubble constant. In the general case with
V( ),
µ2
),
µ2  (which is
dV / d
(which is
dV / d for V =
1/2 µ2
for V =
1/2 µ2
 2) is replaced
by the derivative dV /
d
2) is replaced
by the derivative dV /
d . Equations
(8.2) and (8.3) are the Einstein equations, which can be obtained from
the general equation
. Equations
(8.2) and (8.3) are the Einstein equations, which can be obtained from
the general equation
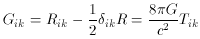
 1 in (8.2) and (8.3)).
1 in (8.2) and (8.3)).
 a(t),
where
a(t),
where  = const << 1. A
point on the surface of this
sphere moves under the influence of the gravitational force produced by
the mass M within the sphere of radius r, so that we have
the equation of motion
= const << 1. A
point on the surface of this
sphere moves under the influence of the gravitational force produced by
the mass M within the sphere of radius r, so that we have
the equation of motion
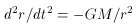
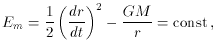
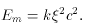
 0, i.e., parabolic motion,
and the hyperbolic
case corresponds to positive Em - infinite
expansion. This is old
stuff, enthusiastically explained in many books (for example, One, Two,
Three, Infinity
(Gamow 1971),
or the famous The First Three Minutes
(Weinberg 1976)).
The next point is that the mass M is defined
differently in (8.5) and (8.6).
0, i.e., parabolic motion,
and the hyperbolic
case corresponds to positive Em - infinite
expansion. This is old
stuff, enthusiastically explained in many books (for example, One, Two,
Three, Infinity
(Gamow 1971),
or the famous The First Three Minutes
(Weinberg 1976)).
The next point is that the mass M is defined
differently in (8.5) and (8.6).
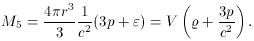
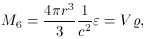
 r3/3 is the volume. Is this a contradiction? The law of the
conservation of mechanical energy is a consequence of the Newtonian
equation for the acceleration. Therefore, at first glance, it would seem
that M5
r3/3 is the volume. Is this a contradiction? The law of the
conservation of mechanical energy is a consequence of the Newtonian
equation for the acceleration. Therefore, at first glance, it would seem
that M5  M6 is impossible. However, the two
equations in fact agree
with one another beautifully, if we remember that the mass inside the
comoving volume only remains constant in the unique case of zero
pressure.
M6 is impossible. However, the two
equations in fact agree
with one another beautifully, if we remember that the mass inside the
comoving volume only remains constant in the unique case of zero
pressure.
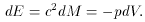
 /3, so
that
/3, so
that  + 3p =
2
+ 3p =
2 , which makes a
small quantitative
change in the expansion law. This was duly accounted for in
nucleosynthesis theory, but nobody much cared about the difference between
M5 and M6.
, which makes a
small quantitative
change in the expansion law. This was duly accounted for in
nucleosynthesis theory, but nobody much cared about the difference between
M5 and M6.
 is
possible with the scalar field is what drew
attention to the subject. Of course, if p =
-
is
possible with the scalar field is what drew
attention to the subject. Of course, if p =
- ,
,
 + 3p =
-2
+ 3p =
-2 is
negative, which means that gravitational attraction is replaced by
gravitational repulsion!!
is
negative, which means that gravitational attraction is replaced by
gravitational repulsion!!
 V, where
V = const a3 and
V, where
V = const a3 and
 =
1/2
=
1/2  2 +
V(
2 +
V( ), one can obtain
(8.1) after performing a few simple mathematical operations. This
reflects a very important property of general relativity. The motion and
transformation of matter and field must obey all the mechanical
equations expressing energy and momentum conservation.
(11)
), one can obtain
(8.1) after performing a few simple mathematical operations. This
reflects a very important property of general relativity. The motion and
transformation of matter and field must obey all the mechanical
equations expressing energy and momentum conservation.
(11)
 - then its equation of
motion is also completely determined by the geometry of space-time.
We shall study two cases in the next few sections: the Higgs
V(
- then its equation of
motion is also completely determined by the geometry of space-time.
We shall study two cases in the next few sections: the Higgs
V( ) with
one maximum and two minima and the linear equation corresponding
to the quadratic potential V = 1/2
µ2
) with
one maximum and two minima and the linear equation corresponding
to the quadratic potential V = 1/2
µ2  2.
2.

 3
a2 (da/dt).
Back.
3
a2 (da/dt).
Back.