


The first conception of the inflationary stage of evolution
Guth (1981)
was based on a definite physical picture formulated by Kirzhnits and then
rigorously developed by
Kirzhnits and Linde (1972).
They used the idea
of a Higgs scalar field with a maximum V(0) = Vmax >
0. In this state,
dV / d |
| =0 = 0, so that
=0 = 0, so that
 = 0 = const and
= 0 = const and
 =
=
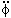 = 0 is a solution.
Obviously, p = -
= 0 is a solution.
Obviously, p = - in
this case. The corresponding solution to the
cosmological equations in the preceding sections, (8.2) and (8.3), are
in
this case. The corresponding solution to the
cosmological equations in the preceding sections, (8.2) and (8.3), are
and
for the open, flat, and closed universe cases, respectively
(Fig. 3). These
three functions are identical for H0t >> 1 when we are
dealing with the
exponential "inflationary" stage in the expansion.
The first idea of the authors was that one begins at the very high
temperature Th at which the thermal oscillations in
the scalar field go over the barrier (Fig. 4):
A total breaking of symmetry at low temperature, with all space
being one domain (with
Qualitatively, the instability is a blessing: the present-day situation
requires that the inflationary stage end at some point! We need the
decrease in V(
However, attempts at quantitative calculations of the perturbations
created during the transition from
where
is called the "closed de Sitter universe." It has the peculiar property of
total homogeneity: all world points, including points with different t,
are equivalent in all respects. This is not easy to see from the metric
written above: it would seem that the section t = 0 would have the
smallest volume, V3 =
2
The flat and hyperbolic de Sitter solutions are not complete. One can
think of them as parts of the complete closed solution with another
choice of t = const hypersurface. This also means that the
transformation
of the 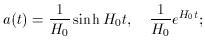
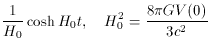
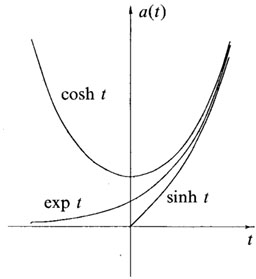
Figure 3.
 2 >
2 >
 2min.
Obviously, due to symmetry, the
average
2min.
Obviously, due to symmetry, the
average  = 0 at the high
temperature Th. The
low-temperature (Tl)
equilibrium state, in which there are small oscillation about the minima,
is show in Fig. 5. We have not included the
excess energy due to the surfaces separating domains with
= 0 at the high
temperature Th. The
low-temperature (Tl)
equilibrium state, in which there are small oscillation about the minima,
is show in Fig. 5. We have not included the
excess energy due to the surfaces separating domains with
 =
=
 min and
min and
 =
-
=
- min in this
figure. The existence of the domain energy is physically obvious: there
is a contribution to the energy that is proportional to (grad
min in this
figure. The existence of the domain energy is physically obvious: there
is a contribution to the energy that is proportional to (grad
 )2, i.e., the
square of the spatial derivatives.
)2, i.e., the
square of the spatial derivatives.
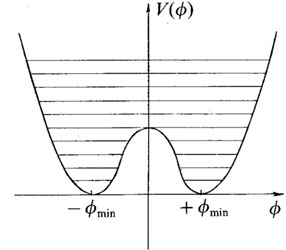
Figure 4.
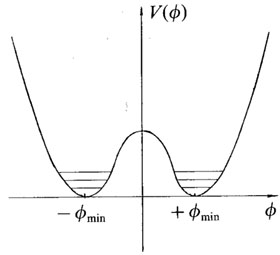
Figure 5.
 =
=
 min, for example) is
thermodynamically
preferred. However, this cannot be achieved in a system with finite
cooling time: the sign of the average
min, for example) is
thermodynamically
preferred. However, this cannot be achieved in a system with finite
cooling time: the sign of the average
 is not correlated in different
regions separated by a large distance. However, supercooling can occur
via the stabilizing effect of the energy connected with the gradient of
is not correlated in different
regions separated by a large distance. However, supercooling can occur
via the stabilizing effect of the energy connected with the gradient of
 .
The energy in the fluctuations and the other fields excited at high
temperature fall off rapidly (proportional to a-4,
i.e., e-4H0t) during the
expansion, so that they become completely negligible compared with
V(0) very soon after the supercooling begins. The oscillations are
damped out during the supercooling by the expansion, while
.
The energy in the fluctuations and the other fields excited at high
temperature fall off rapidly (proportional to a-4,
i.e., e-4H0t) during the
expansion, so that they become completely negligible compared with
V(0) very soon after the supercooling begins. The oscillations are
damped out during the supercooling by the expansion, while
 fluctuates near the maximum (Fig. 4). This is
the unstable situation that gives rise to the inflationary expansion.
fluctuates near the maximum (Fig. 4). This is
the unstable situation that gives rise to the inflationary expansion.
 ) from V(0) to
Vmin(
) from V(0) to
Vmin( min)
in order to reheat the
Universe, to give rise to the relic radiation, protons, neutrons,
galaxies, stars, and life.
min)
in order to reheat the
Universe, to give rise to the relic radiation, protons, neutrons,
galaxies, stars, and life.
 = 0 to
= 0 to
 =
=
 min give bad results.
For the mathematically oriented reader: the basic solution for a closed
universe,
min give bad results.
For the mathematically oriented reader: the basic solution for a closed
universe,
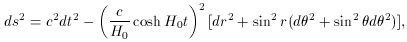
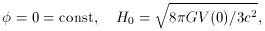
 2a3(0) =
2
2a3(0) =
2 2c3 /
H30. However, this is not true,
since there is a coordinate transformation that makes the other world
points lie on other minimal-volume hypersurface t' = 0.
2c3 /
H30. However, this is not true,
since there is a coordinate transformation that makes the other world
points lie on other minimal-volume hypersurface t' = 0.
 = 0 unstable state into hot
plasma is purely probabilistic
in this model. These important details can be found in the paper by
Grishchuk and the author in the proceedings of the Moscow conference
on quantum gravity (Grishchuk and Zel'dovich 1982).
= 0 unstable state into hot
plasma is purely probabilistic
in this model. These important details can be found in the paper by
Grishchuk and the author in the proceedings of the Moscow conference
on quantum gravity (Grishchuk and Zel'dovich 1982).