When a photon is scattered by an electron, the energy and direction of motion of both the photon and the electron are usually altered. The change in properties of the photon is described by the usual Compton scattering formula
where the electron is assumed to be at rest before the interaction,
For low-energy photons and mildly relativistic or non-relativistic
electrons,
Scatterings of this type will also cause Sunyaev-Zel'dovich effects
from the relativistic plasma of radio galaxies. The lobes of radio
galaxies emit strong synchrotron radiation, and must contain
electrons with Lorentz factors
In this thermal scattering limit,
the interaction cross-section for a microwave background photon
with an electron need not be described using
the Klein-Nishina formula,
but rather the classical Thomson cross-section formula which results
in the limit
where the electron velocity ve =
(Chandrasekhar 1950; Wright 1979), and
the change of photon direction causes the scattered photon to appear
at frequency
with µ' = cos
It is conventional
(Wright 1979;
Sunyaev 1980;
Rephaeli 1995b)
to express the resulting scattering in terms of the logarithmic frequency
shift caused by a scattering, s (Sunyaev uses u for a related
quantity),
when the probability that a single scattering of the photon causes a
frequency shift s from an electron with speed
Using (23-25), this becomes
where µ' can be expressed in terms of µ and
s as
(from equations 25 and 26), and the integral is
performed only over real angles, so that
in (28). The integration can be done easily,
and Fig. 4 shows the resulting function for several
values of
increases because increasing
and ' are the photon energies
before and after the interaction, and 
12 is the angle by which the
photon in deflected in the encounter (see Fig. 3).
Figure 3. The scattering geometry, in the frame of
rest of the electron before the interaction. An incoming photon, at
angle 
relative to the
xe axis, is deflected by angle
12, and emerges after
the scattering at
angle ' with almost unchanged energy
(equation 21). In the observer's frame,
where the electron is moving with velocity 
c along the
xe axis, the photon changes energy by an amount depending on
and the angles
and
'
(equation 25).
<<
me c2 and the scattering is
almost elastic (' = ). This limit
is appropriate for the scatterings in clusters of galaxies that
cause the Sunyaev-Zel'dovich effect, and causes a considerable
simplification in the physics. Although the scatterings are usually
still referred to as inverse-Compton processes, they might better be
described as Thomson scatterings in this limit.
e 
108. In the
rest frames of such electrons the microwave background
radiation appears to have a peak at photon energies
~ 0.1 me c2, and the assumption of elastic
scattering
will be inappropriate. Little theoretical work has been done on the
spectrum of the scattered radiation in this limit, but see
Section 5.
' -> . Then if the
geometry of the collision process in the electron rest frame is as
shown in Fig. 3, the probability of a scattering with
angle is
c, and
µ = cos. The
probability of a scattering to angle
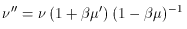
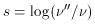
' is
'.
c is
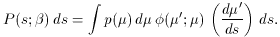
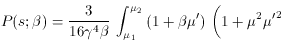
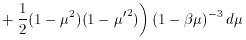
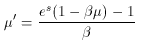
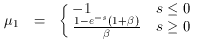
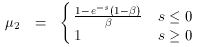
. The
increasing asymmetry of P (s; ) as
increases is caused by relativistic beaming, and the width of the
function to zero intensity in s,
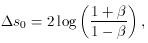
causes the
frequency shift related to a given photon angular deflection to
increase.
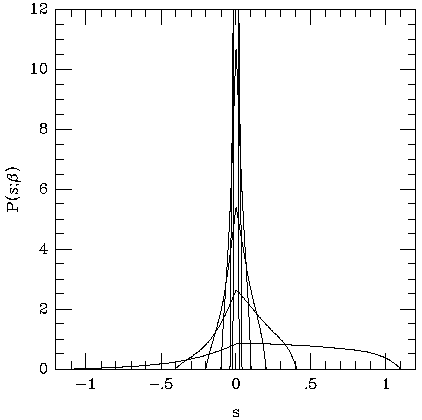
Figure 4. The scattering probability function
P (s; ), for
= 0.01, 0.02,
0.05, 0.10, 0.20, and
0.50. The function becomes increasingly asymmetric and broader as
increases.