1.2. Overview of Relevant Cosmological Equations

1.2.1. The Robertson-Walker Metric

To place the Hot Big Bang model into a physical context necessitates a sensible mathematical formulation. To assist with this formulation we assume that the universe on a large scale is both homogeneous and isotropic. This assumption is known as the Cosmological Principle and the observed isotropy of the expansion and the CMB are strong testaments to its validity. If we accept this principle to be valid, then our task is to construct a geometrical model of the Universe that explicitly incorporates large scale homogeneity and isotropy. Ideally, this model should be described by a relatively small number of parameters, all of which can be observationally determined. Much of this book is devoted to a modern discussion of attempts to determine these parameters from observations. However, before doing that we must describe the framework that allows observations to be directly connected to our cosmological model.

To begin with, we note that General Relativity is a geometrical theory concerning the overall curvature of space-time. Within that context we seek to specify the coordinate properties of a homogeneous, isotropic, expanding Universe. If we are to fully describe the Universe in geometrical terms, we must derive a metric which describes the coordinate paths that objects are allowed to take. In deriving this metric we must introduce the concept of an event. An event is something which occurs at a certain place at a certain time. Hence all events in the universe can be thought of as occurring in a four-dimensional spacetime continuum, with three spatial dimensions and one dimension of time. To compute the separation between any two events in spacetime, it is necessary to specify the metric. As a simple example, consider the surface of a sphere, which can be thought of as a two-dimensional analogue to the four-dimensional spacetime. Using simple spherical trigonometry, the metric of a sphere can be written as

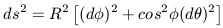
(10)

where ds denotes the distance between two points on the surface of the sphere, R is the radius of the sphere, and d and d are the difference in latitude and longitude between the two points (measured in radians). With this expression, it is possible to compute the separation between any two points along the surface of the sphere. Hence the geometry of the sphere and the physical specification of events is completely described by its metric.

The geometry of four-dimensional spacetime is described by an analogous metric. However, instead of computing the distance between two points on the surface of a sphere, we wish to compute the separation between two events, which involves both space and time. Special relativity allows one to show that the spacetime interval, ds, between two events which occur near each other in flat space is given by

(11)

where dt is the time interval between the two events (as determined by an inertial observer), c is the speed of light, and dx, dy, dz correspond to the separation between the two events in each of the three spatial dimensions. Note that, unlike the metric for an ordinary sphere, the spacetime metric need not always be positive. The geometry of spacetime is completely specified by equation 11. A geodesic is the shortest interval between any two points in spacetime.

Equation 11 assumes a flat Euclidean geometry, in which initially parallel lines always remain parallel. However, according to Einstein's theory of General Relativity, spacetime is curved by gravity, which is a manifestation of the energy density of matter. The separation between two events will therefore depend on the curvature of spacetime. This is schematically shown in Figure 1-6 for three specific curvatures.

Figure 1-6: Schematic representations of the possible geometries of space time. These are two-dimensional analogs of curved space. In positively curved space the sum of the angles of a projected triangle on that surface is greater than 180 degrees while in negatively curved space it is less than 180 degrees

For a homogeneous and isotropic universe, the most general metric in curved spacetime is the Robertson-Walker metric, which was first proposed in 1934. Expressed in spherical polar coordinates (r, , ), this metric takes the form

(12)

where R(t) is the universal scale factor which describes the time evolution of the universal expansion, k denotes the curvature of spacetime (k = -1, 0, 1 for negative, zero, or positive curvature), and the coordinate r is comoving with the universal expansion. If we imagine a particle at rest with a given set of coordinates r, , , then as long as no external forces operate on this particle. then the particle remains at those coordinates. These coordinates are said to be comoving coordinates. They are related to physical coordinates through the scale factor,

(13)

The Robertson-walker metric is independent of any particular gravitational theory. Gravity enters through the scale factor R(t) and the curvature constant k; the distance between any two spacetime events therefore depends on what specific cosmological model is adopted. This specific cosmological model is determined by the values of R(t) and k which can be observationally determined.