


1.2.2. The Dynamics of an Expanding Universe
Now that we have specified the metric that holds in a homogeneous and isotropic Universe, the next step is to consider the dynamics of an expanding Universe. Since the Universe has mass, then at all times the expansion must compete against the combined (attractive) gravitational acceleration of that matter. In Newtonian mechanics this acceleration is given by
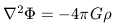
| (14) |
where  is the matter
density and
is the matter
density and  is the
gravitational potential. This equation is historically known
as Poisson's equation.
is the
gravitational potential. This equation is historically known
as Poisson's equation.
This simple equation for gravitational acceleration does not apply in the very early Universe due to the presence of very high energy photons. The majority of the mass-energy in the early Universe is in the form of radiation moving at c. The high radiation pressure drags the matter along with it and effectively counters the tendency for the matter to collapse. In this sense, the Universe acts as a relativistic fluid with a pressure term whose behavior is not adequately described by Newtonian mechanics. The details about the Stress-Energy tensor in Einstein's field equations are beyond the scope of this book (for reference see Weinberg 1972; Peebles 1993) but they lead to a generalization of equation 14:
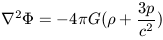
| (15) |
where p / c2 is the pressure (which we subsequently
set to p; c=1) and the combined term
 +3p
effectively becomes the gravitational mass density
+3p
effectively becomes the gravitational mass density
 g which produces
the net gravitational acceleration of material that decreases the
expansion rate.
g which produces
the net gravitational acceleration of material that decreases the
expansion rate.
If we now consider a sphere of radius rs and volume V which has some mean gravitational mass density within it, the total mass of that sphere is given by
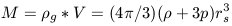
| (16) |
The acceleration at the surface of the sphere is given by Newton's law of gravitation as -GM / Rs2. Multiplying equation 13 by the term -G / Rs2 then yields
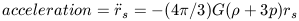
| (17) |
where 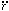 s2
refers to the second time derivative of
the spatial coordinate, rs (the first time derivative
s2
refers to the second time derivative of
the spatial coordinate, rs (the first time derivative
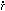 s
is a velocity). Equation 17 is a standard equation in General Relativity
and it describes the evolution (e.g., expansion or contraction) of a
homogeneous and isotropic mass distribution. Within this sphere
there is some net energy, En. This energy is
s
is a velocity). Equation 17 is a standard equation in General Relativity
and it describes the evolution (e.g., expansion or contraction) of a
homogeneous and isotropic mass distribution. Within this sphere
there is some net energy, En. This energy is
 V. If the material
enclosed in rs moves so that it changes
rs then En changes
in accordance with how much work is done by the pressure of the fluid on
the surface of the sphere. By conservation of energy we then have
V. If the material
enclosed in rs moves so that it changes
rs then En changes
in accordance with how much work is done by the pressure of the fluid on
the surface of the sphere. By conservation of energy we then have
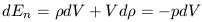
| (18) |
Equation 18 states that the change in net energy is exactly
equal to the change in volume multiplied by the pressure. Rearranging
the terms involving dV and defining the volume as V =
(4 / 3) rs3
(
/ 3) rs3
(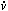 =
3
=
3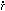 s
rs2)
s
rs2)
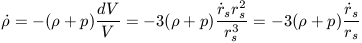
| (19) |
Solving for p in equation 19 and plugging that solution in equation 17 yields the following differential equation
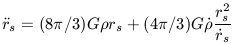
| (20) |
This is a messy differential equation. If we multiply both
sides by the term 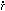 s
and choose units such that
the quantity (4
s
and choose units such that
the quantity (4 / 3)G = 1 and let
rs be x then we arrive at the following functional form
/ 3)G = 1 and let
rs be x then we arrive at the following functional form
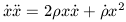
| (21) |
Now the right hand side is just
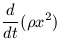
| (22a) |
and the left hand side is just
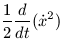
| (22b) |
Integrating both sides over time then yields
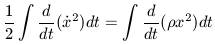
| (22c) |
Switching back to normal units yields the first integral of equation 20:
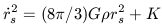
| (23) |
where K is a constant of integration which we can identify with the curvature term in the Robertson-Walker metric. Equations 17 and 23 are the main equations of this cosmological model.
If we consider the case of a static Universe where rs is, by definition, constant and hence all derivatives are zero then equations 17 and 23 become
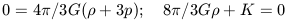
| (24) |
Since the mass density
 must be positive
then to satisfy
the constraint of a static Universe p must be negative. Since normal
matter cannot have negative pressure, Einstein introduced the cosmological
constant
must be positive
then to satisfy
the constraint of a static Universe p must be negative. Since normal
matter cannot have negative pressure, Einstein introduced the cosmological
constant  into the field
equations to serve as the source of
negative pressure. In the static Universe
into the field
equations to serve as the source of
negative pressure. In the static Universe
 balances the
net gravitational acceleration. But the Universe is not static, it
is expanding according to the expansion scale factor R(t) given in
equation 13. Our hypothetical sphere radius rs will then be
different at some later time, t, such that
balances the
net gravitational acceleration. But the Universe is not static, it
is expanding according to the expansion scale factor R(t) given in
equation 13. Our hypothetical sphere radius rs will then be
different at some later time, t, such that
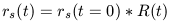
| (25) |
Equation 17 now becomes
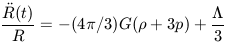
| (26) |
where the first of the two terms on the right hand side is for the
pressure and density of ordinary matter (e.g., stars and galaxies) and
the second term includes the contribution of the Cosmological Constant.
Equation 26 then describes the relativistic acceleration of the expansion,
which in principle, can be dominated by
 at late times as
at late times as
 and p
decrease with time while
and p
decrease with time while
 stays nearly constant.
This in fact is the physical manifestation of non-zero
stays nearly constant.
This in fact is the physical manifestation of non-zero
 .
In this case, the Universe evolves from being radiation dominated, to
being matter dominated, to being vacuum energy dominated.
.
In this case, the Universe evolves from being radiation dominated, to
being matter dominated, to being vacuum energy dominated.
The second of the two cosmological equations, equation 23, can now be expressed as
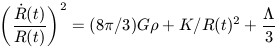
| (27) |
Equation 27 demonstrates that the rate of change of the scale
factor R(t) is affected by three things: the net gravitational force
acting to decelerate the Universe which is determined by the matter
density ( ); a
curvature term related to the geometry of the Universe (K = 0
is flat; K = +1 is positive curvature, K = -1 is negative curvature);
and a term related to the vacuum energy which acts as a long range
repulsive force.
); a
curvature term related to the geometry of the Universe (K = 0
is flat; K = +1 is positive curvature, K = -1 is negative curvature);
and a term related to the vacuum energy which acts as a long range
repulsive force.
The quantity 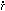 (t) /
R(t) is the rate of change of
the scale factor and is parameterized as H, the Hubble constant. H
is a measurable quantity. For the case of
(t) /
R(t) is the rate of change of
the scale factor and is parameterized as H, the Hubble constant. H
is a measurable quantity. For the case of
 = 0 if we can measure
H and
= 0 if we can measure
H and  (the present
day mass density of the Universe) then we will have
solved
for K / R(t)2 and hence, under the Robertson-Walker
metric, completely
specify the geometry of spacetime. In this way, we have formulated
a mechanism where observations can fully determine the cosmological model -
there are no hidden variables. In
the special case where the curvature of the Universe is zero (K = 0) and
(the present
day mass density of the Universe) then we will have
solved
for K / R(t)2 and hence, under the Robertson-Walker
metric, completely
specify the geometry of spacetime. In this way, we have formulated
a mechanism where observations can fully determine the cosmological model -
there are no hidden variables. In
the special case where the curvature of the Universe is zero (K = 0) and
 = 0, we have
= 0, we have
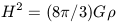
| (28) |
The rate of change of  with time is given by equation 19
which can be rewritten in terms of the scale factor R(t) as
with time is given by equation 19
which can be rewritten in terms of the scale factor R(t) as
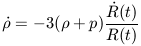
| (29) |
With zero pressure (p = 0) we have
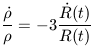
| (30) |
The only solution to this is that

 R(t)-3
(
R(t)-3
( =
-3R(t)-4
=
-3R(t)-4
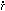 (t) ). Note that the expression
(t) ). Note that the expression

 R(t)-3 is also the one that satisfies the condition that
the mass within a sphere (4
R(t)-3 is also the one that satisfies the condition that
the mass within a sphere (4 / 3
/ 3
 (t)
R(t)3) as a function of time
remains constant. From equation 28 we then have
(t)
R(t)3) as a function of time
remains constant. From equation 28 we then have
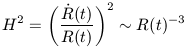
|
which is only satisfied if the scale factor R(t) goes as
t2/3. The quantity
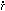 (t) / R(t) = H is
now
(t) / R(t) = H is
now
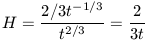
|
Thus, in the zero curvature case, the expansion age of the Universe is
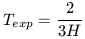
| (31) |
If space is devoid of mass (and hence is negatively curved)
then we can set  = 0
to yield
= 0
to yield
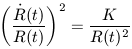
|
which has a solution of the form R(t) goes as t and the
expansion age tends to H-1. In either case, observations
which determine H also then
reveal the approximate age of the Universe. The fact that the
ages of the oldest stars in the Universe are in the range
.67 H-1 - 1.0 H-1 has led some
(e.g.,
Liddle 1996) to
claim that this forms another observational pillar for the
Hot Big Bang theory. However, its important to emphasize that
the expansion age of the Universe is only
 H-1 in the
special case where
H-1 in the
special case where
 = 0. For
= 0. For

 0, the relationship with
H-1 is considerably more complicated as
0, the relationship with
H-1 is considerably more complicated as
 acts to make the
expansion rate decrease more slowly as its a repulsive force. In
fact, it can be shown that
acts to make the
expansion rate decrease more slowly as its a repulsive force. In
fact, it can be shown that
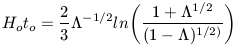
|
(see Kolb and Turner 1991; Krauss and Turner 1994) in the case of
inflation (see chapter 4) in which
 +
+
 = 1 (where
= 1 (where
 = 0 is the usual
case). H0t0 > 1 is satisfied for
= 0 is the usual
case). H0t0 > 1 is satisfied for
 > 0.74. Hence, to reconcile
the possible age problem by invoking non-zero
> 0.74. Hence, to reconcile
the possible age problem by invoking non-zero
 requires a value of
requires a value of
 which is
in significant excess of
which is
in significant excess of
 meaning that at the present epoch
the Universal is dominated by Vacuum Energy.
meaning that at the present epoch
the Universal is dominated by Vacuum Energy.
The final useful relation to derive is the expression for the critical density of the Universe. This is defined as the density which is required to eventually halt, by mutual gravitational contraction, the expansion of the Universe. Like the previous derivations, this one again can be done in terms of energy conservation assuming the Universe is a sphere of uniform density. In this case the total mass is given by equation 16 with p = 0. Consider now a galaxy trying to escape the surface of this sphere. Its potential energy is given by
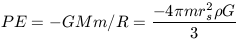
| (32) |
and its kinetic energy is given by
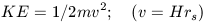
| (33) |
The velocity, v, of this galaxy is determined by the expansion rate expressed by the Hubble law. Thus v = Hrs. To escape this sphere of radius rs, KE must exceed PE so we have the critical condition
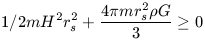
| (34) |
we can readily eliminate m and rs2 to arrive at the expression for critical density:
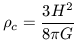
| (35) |
The critical density is not dependent upon the size and
mass of the Universe but only on its expansion rate. If the
real density of Universe exceeds
 c then the
Universe is destined
to collapse. The Universe can not collapse at early times due to
entropy production and the associated high radiation pressure. Equation
35 strictly only applies in the matter dominated era.
c then the
Universe is destined
to collapse. The Universe can not collapse at early times due to
entropy production and the associated high radiation pressure. Equation
35 strictly only applies in the matter dominated era.