2.1. Overview:
In Chapter 1, we were able to parameterize the
important equations
by the observational parameter H =
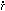(t) / R(t)
which specifies the rate of change of the scale factor R(t).
This rate of change today is known as he Hubble Constant (H0)
which is a measure of the present day expansion rate
of the Universe. Since the universe has mass, then the expansion
rate is slowing down do to gravitational attraction so the value
we measure for H today, is different (smaller) than its value
in the past. The importance of determining an accurate value
for H0 with respect to our cosmological model is threefold:
It specifies the expansion
age of the Universe and
therefore provides a consistency check with other, independent
ways of age dating the Universe. As we will later see,
current values of H0 indicate an expansion age which is
less than the ages of the oldest stars, which is clearly
physically impossible.
It specifies the value for
the critical density of
the Universe which, when compared to the observed value (a
difficult parameter to measure) determines if the Universe is
open (expands forever) or closed (expands to a maximum radius
and then contracts)
It sets the overall scale
size of the Universe.
In this chapter, we summarize the many observational techniques which have been employed by various groups using the best available telescopes, including the Hubble Space Telescope (HST) We will go through a rigorous, step-by-step approach on how the extragalactic distance scale is determined. Although some of these steps are tedious, it is necessary to understand them in some detail in order to properly sort out the current controversy of the value of H0. The goal is to measure H0 to an accuracy of ± 10% in order to distinguish between various cosmological models. As will be emphasized here, this goal is not yet attainable, and may never be using current methods of measuring distances to external galaxies.
In addition to the determination of H0 there are other parameters which can be measured. While we defer rigorous discussion of these to later chapters, we introduce them here:
The actual density of the
Universe (
). If the
exceeds
the critical density the Universe is said to be closed. If the
is less than the critical density the Universe is said to be open,
meaning that it will expand forever. In our cosmological equations
of Chapter 1,
is an
important parameter. As will be seen in
Chapters 3 and 4,
estimates of
vary by a factor of
10 whereas
estimates of H0 vary by a factor of 1.8. Thus, the dominant
observational uncertainty in our determination of the spatial
curvature of the Universe is the measurement of
.
Whether
is zero or not. In the cosmological
equations of Chapter 1
appears as a long range repulsive
term and physically acts like a source of negative pressure. As
will be discussed in Chapter 4,
represents the remaining
vacuum energy after inflation has ended. While convenient,
does not necessarily have to be zero. Indeed, a positive value of
contributes vacuum-energy to
the Universe which allows the
expansion rate to increase with time. In practice, this means
that the Universe has an expansion age
10-20% larger than
H0-1.
Age estimations of the
Universe: A consistent model is
one in which the expansion age, as inferred by
measuring H0 (and
) agrees with an
independently estimated
age for the Universe. The most readily available independent estimate
comes from the age of the oldest stars as found in Globular Clusters.
This is the subject of much research and much uncertainty associated
with how stars evolve and how much convective mixing of material is
important in later stages of evolution. In general, mixing of
material down into a stellar core increases stellar lifetimes. The
broadest range of estimates of Globular Cluster ages is
tglob =
10-18 Gyrs (Flannery and Johnson 1980; Stetson et al. 1996) but
in recent years age estimates have converged to the 15-18 Gyr range.
A recent estimate is that of Bolte and Hogan (1995) who derive
tglob = 15.8 ± 2.1 Gyrs. Jiminez and Padoun (1996) use
a more refined, but controversial technique, to fix the ages at
tglob = 16.0 ± 0.5 Gyrs.
Chaboyer (1996) concludes that the
best age is 14.6 ± 1.7 Gyrs with a 95% confidence lower limit of
12.2 Gyr.
Moreover, a new generation of stellar models that take into account Helium mixing have just been published by Sweigart (1997). These models suggest that these ages of 15-17 Gyrs should be revised downward. While it is well beyond the scope of this book to delve into stellar interior models, suffice it to say that globular cluster ages remain highly model dependent and we still don't understand the physics of the interiors of low mass, metal-deficient stars, well enough to do accurate age dating. While Sweigart's recent results are likely to be controversial, (for instance they favor a steeper relation between [Fe/H] and Mv for Horizontal Branch stars than is actually observed) they should serve mostly as a reminder that globular cluster ages are not caste in stone. Furthermore, as pointed out in Chaboyer et al. (1997), it is likely that their is a range of formation times, and hence ages for Galactic Globular clusters. Hence, it will be necessary to age date most of the halo population of Globular Clusters in order to find the oldest ones.
Another means to age date the Galaxy, and hence the Universe by adding a reasonable time for galaxy formation, is to make use of nuclear cosmochronometers based on the decay of long lived radioactive elements. Age dating via this technique is also quite model dependent since nuclear cosmochronology is quite sensitive to the history of very heavy element creation and the amount of infall or mixing of enriched gas with primordial gas in our Galaxy. Current models give age estimates in the range 13-21 billion years (see Cowan et al. 1991) which is consistent with the age estimates from Globular Cluster stars. A more recent treatment of the problem by Chamcham and Hendry (1996) suggests that a minimum age for the Galactic disk is 12 billion years. Their preferred model gives an age of 13.5 Gyr but this number is subject to systematic uncertainties.
Perhaps the most important aspect of alternate ways of age dating the Galaxy is the establishment of a minimum age. From nuclear cosmochronology this minimum age is 12 Gyr. Another means of establishing a minimum age is to identify the coolest white dwarfs and to use white dwarf cooling theory (see Winget et al. 1991) to determine ages. Of course, it is difficult to observationally identify cool white dwarfs and therefore finding the coolest/oldest one in the Galaxy is an elusive goal. Furthermore, due to their intrinsic faintness, searches for cool white dwarfs are generally restricted to the Galactic disk, although recently HST observations of halo fields are being used to find halo white dwarfs (see von Hippel et al. 1996). The basic result to date from these searches is the rather firm minimum age for the Galactic disk of 9-10 Gyrs (see Winget et al. 1991). Since the disk is the last galactic component to form, the age of the Galactic halo could be considerably larger.
Finally, there potentially is a very interesting constraint that can
be put on the age of the Universe from observations of high redshift
galaxies. If a spectrum of a z
3 galaxy reveals the presence of
strong stellar absorption lines which is indicative of a stellar population
of galaxies a few billion years old, then, necessarily the Universe must
be a few billion years old by this redshift. The age as a function of
redshift is given by
|
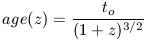
where t0 ~ tglob is the age of the
Universe. At z = 3, the age is
then 1/8 the age of the Universe. The discovery of a galaxy at z = 3 with
a stellar population of 2
billion years then constrains t0 to
be at least 16 Gyr. Dunlop et al. (1996) have discovered
a galaxy with z = 1.55 that does have spectral features indicative
of a stellar population of age a few Gyr. Their preferred age is
3.5 billion years. At this redshift the Universe is 1/4 of its present
age which again suggests a minimum age of 16 Gyr, presuming this galaxy
took a few hundred million years to form.
Even stronger evidence for
relatively old galaxies at high redshift is provided by the work of
Steidel et al. (1996). For galaxies which are dominated by UV emission,
there should be a pronounced break in the energy distribution at 912
Angstroms as emission at wavelengths shorter than this is completely
absorbed by neutral hydrogen. This absorption edge is known as the
Lyman limit. At redshifts of 3-3.5, the Lyman limit is redshifted into
a ground based U (ultraviolet)-filter at wavelength
3500-4000 Å.
Hence, a faint galaxy which "disappears" when observed through this filter
is a candidate for a high redshift, star forming galaxy. While Steidel et al.
have found a number of actively star forming galaxies at this redshift,
they have also discovered, through spectroscopic follow-up, have absorption
lines indicative of an older stellar population perhaps with mean age
as great as 2 billion years. At the very least, the Steidel et al.
result shows that some galaxies at redshifts 3-3.5 clearly have already
produced a significant number of stars.