


3.1. Overview and caveats
Regardless of the specific origin of structure in the Universe, its
existence allows us to probe the distribution of matter on various
size scales from which origin scenarios can be reconstructed. At
a minimum, observations clearly show that 1) the mass in the Universe
is confined to discrete units called galaxies, 2) these galaxies
are not distributed uniformly but rather are highly clustered on
a variety of size scales, and
3) there are large regions that are apparently devoid of mass.
Due to this complexity, it is rather difficult to determine what
represents a fair volume of sampling of this structure. Nevertheless,
an accurate measurement of the mass distribution over a fair volume
will provide us with observational constraints on
 , the
other cosmological parameter of interest. Furthermore, the distribution
of mass on both small and large scales provides a stringent constraint
on any physical theory which is
used to predict the formation and growth of such structure. This is
discussed in detail in Chapter 5.
, the
other cosmological parameter of interest. Furthermore, the distribution
of mass on both small and large scales provides a stringent constraint
on any physical theory which is
used to predict the formation and growth of such structure. This is
discussed in detail in Chapter 5.
The measurement of large scale structure (LSS) from observations is subject to two important caveats:
1. On a large scale the Universe exhibits uniform isotropic expansion. Any departure from homogeneity produces a region of overdensity (as well as one of underdensity) which can serve to retard the expansion locally. This effect is well known in the nearby Universe as our expansion motion away from the Virgo cluster is being retarded by its presence. In the early Universe these mass inhomogeneities, if they existed, would have a similar local effect on the copious photon field.
Suppose there exists a density
contrast 
 /
/
 =
=
 x over some comoving
scale x.
The physical size of this region depends upon epoch in the Universe
and hence is driven by the scale factor a.
Thus the "radius" is ax. The total amount of
Mass within that radius is
x over some comoving
scale x.
The physical size of this region depends upon epoch in the Universe
and hence is driven by the scale factor a.
Thus the "radius" is ax. The total amount of
Mass within that radius is
 x M. The
gravitational potential which arises from this density enhancement is
fully specified in a Newtonian manner:
x M. The
gravitational potential which arises from this density enhancement is
fully specified in a Newtonian manner:
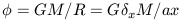
| (1) |
Since  x M is
not a quantity that is easily inferred
from observations it is better to rewrite equation 1 in
terms of the matter density
(
x M is
not a quantity that is easily inferred
from observations it is better to rewrite equation 1 in
terms of the matter density
( ). Since we have a
density contrast then the relevant density is
). Since we have a
density contrast then the relevant density is
 x
x
 b where
b where
 b
is the average, background mass density. We now have
b
is the average, background mass density. We now have

| (2) |
At very early times, the Universe is essentially critical,
with the critical density defined in equation 1.35. From this we
can substitute for
 b to yield
b to yield
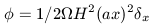
| (3) |
The scale factor , a, grows
as H-2/3. In addition, density fluctuations grow
linearly with the scale factor and the overall rate of growth is
a function of 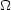 (see
Chapter 5). So
we have
(see
Chapter 5). So
we have  x directly
proportional to a and
H2 goes as a-3. Substituting into
equation 3 shows
that there is no time dependence on the gravitational
potential which is associated with the mass fluctuation.
The fluctuation grows against an expanding background in such
a manner so as to keep
x directly
proportional to a and
H2 goes as a-3. Substituting into
equation 3 shows
that there is no time dependence on the gravitational
potential which is associated with the mass fluctuation.
The fluctuation grows against an expanding background in such
a manner so as to keep  constant.
constant.
Radiation which is
contained within this fluctuation but escapes this particular potential
is gravitational redshifted by an amount which is proportional
to  , the depth of the potential
well that the photons have
to climb out of. This loss of energy causes those photons
to have slightly lower temperature than the photons that did not escape
from this potential. In this way, the CMB radiation has
temperature fluctuations which are directly proportional
to the density fluctuations. This is known as the Sachs-Wolfe
effect (Sachs and Wolfe 1967). If density fluctuations in the
early Universe were present (to produce the structure we observe
today), the Sachs-Wolfe effect is an inescapable consequence.
What remains to be determined is the overall amplitude of the
temperature fluctuations.
, the depth of the potential
well that the photons have
to climb out of. This loss of energy causes those photons
to have slightly lower temperature than the photons that did not escape
from this potential. In this way, the CMB radiation has
temperature fluctuations which are directly proportional
to the density fluctuations. This is known as the Sachs-Wolfe
effect (Sachs and Wolfe 1967). If density fluctuations in the
early Universe were present (to produce the structure we observe
today), the Sachs-Wolfe effect is an inescapable consequence.
What remains to be determined is the overall amplitude of the
temperature fluctuations.
For simplicity we assume the temperature fluctuations have a linear dependence on the potential:
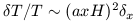
| (4) |
For the present epoch and we use an averaging scale a0 x equal to the Hubble length (c H0-1) so that
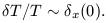
| (5) |
The Hubble length defines a distance over which light
can travel given the expansion age of the Universe. This region is
called a horizon as it represents a causally connected portion
of the Universe. Material that exists outside of an observer's
horizon can not communicate with that observer unless communication
occurs at faster than light speed. However, since the Universe
is expanding, all observer's horizons increase with time and hence
that material will eventually be inside the observer's horizon.
Note that in an open Universe, H0 tends towards zero and the
horizon (c H0-1) tends towards
infinity. Furthermore,
the angular size of our horizon is a strong function of redshift
(and 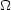 ). At the time of
recombination, when the CMB signal
can be observed, the angular size of the horizon is
). At the time of
recombination, when the CMB signal
can be observed, the angular size of the horizon is
 2°.
2°.
The Cosmic Microwave Background Explorer (COBE) had an angular
resolution of  7.5 degrees
and hence made measurements
over many scales of average size a0 x (e.g. over many
horizons).
The measured COBE anisotropy, on this scale, is
7.5 degrees
and hence made measurements
over many scales of average size a0 x (e.g. over many
horizons).
The measured COBE anisotropy, on this scale, is
 T / T
T / T
 10-5.
So within any one horizon,
10-5.
So within any one horizon,
 T / T is ~ 0 indicating
that conditions of homogeneity
and isotropy are maintained but there is a small fluctuation signal
when averaged over many horizons.
The challenge is to understand how the rich
variety of structure we observe today can be reconciled with
these small temperature fluctuations.
In principle, structure on all scales has arisen from a perturbation
spectrum which had an average density contrast of 10-5
at the time of recombination. Thus, under the gravitational instability
model for the formation of LSS (see Chapter 5)
, the primordial density fluctuation spectrum is
directly reflected by the fluctuations in the CMB.
T / T is ~ 0 indicating
that conditions of homogeneity
and isotropy are maintained but there is a small fluctuation signal
when averaged over many horizons.
The challenge is to understand how the rich
variety of structure we observe today can be reconciled with
these small temperature fluctuations.
In principle, structure on all scales has arisen from a perturbation
spectrum which had an average density contrast of 10-5
at the time of recombination. Thus, under the gravitational instability
model for the formation of LSS (see Chapter 5)
, the primordial density fluctuation spectrum is
directly reflected by the fluctuations in the CMB.
2. There are serious concerns over how one best measures LSS in the local Universe. The simplest way is to use galaxies as tracers of the mass. By determining, through redshift surveys, the three dimensional galaxy distribution then one gets a direct measure of the mass distribution under the assumption that galaxies are fair tracers of this distribution. On small scales, there is a well-established relation between local galaxy density and galaxy type in the sense that dense systems like elliptical galaxies are preferentially found in regions of high galaxy density (e.g. clusters) of galaxies while less dense systems (disk galaxies) are found in lower density regions. Hence, some care must be taken in redshift surveys to sample a range of galaxy types to ensure that all environments are probed.
In Chapter 6 we discuss the properties of low surface brightness (LSB) galaxies. In general, such galaxies are missing from optical redshift surveys as its difficult to acquire a good optical spectrum of such a diffuse system. If LSB galaxies are distributed in a fundamentally different manner as galaxies of higher surface brightness, then bias could be present in optical redshift surveys. This point has been investigated in some detail (Bothun et al. 1986, Bothun et al. 1993, Impey et al. 1996) and on scales greater than or equal to ~ 2h-1 Mpc there is no bias. This is true also for redshift surveys that use either emission line galaxies (e.g. Aldering et al. 1988) or IRAS galaxies (e.g. Fisher et al. 1995). The conclusion is that all different kinds of galaxies adequately trace structure on large scales and in fact, it is this very insensitivity of large-scale structure to galaxy properties that allows it to be determined from redshift surveys. The only bias that exists is that elliptical galaxies are preferentially confined to virialized cores and therefore are not good tracers of structure on scales larger than that of individual galaxy clusters. However, this also means that elliptical galaxies are rare and are a minority population of redshift surveys.
In principle, there is a more direct way to measure the mass distribution. Any mass overdensity will produce a perturbation of the expansion velocity of a galaxy which is near it. The extreme case, that of a virialized cluster, represents a situation where the perturbation is so severe that the expansion velocity is completely overcome so that the cluster in fact, does not expand with the rest of the Universe. Since this perturbation is gravitationally induced then its effect on neighboring galaxies decreases as R-2. Any difference between expansion velocity and observed velocity is called the peculiar velocity. If an all sky peculiar velocity map of a fair volume of the Universe can be made, then under the caveat that these peculiar motions are gravitationally induced, the velocity residuals in this map will point directly at mass concentrations. If there was no bias between light and mass, then this peculiar velocity map would point at observable mass concentrations (e.g. clusters of galaxies). This is because both the intensity of light and the gravitational force fall of as R-2 - you should fall where the light is.