2.3.4. Distances to Local Group Galaxies

The foundation of the extragalactic distance scale lies in obtaining distances to a sample of nearby galaxies that have (hopefully) the same range of properties as more distant galaxies. For instance, to pick an absurdly simple situation - suppose all spiral galaxies had the same exponential scale length. If this were true, then a measurement of the distance to the Andromeda galaxy would then directly secure distance measurements to all other spiral galaxies. Alas, things are not so simple and distances to a variety of different galaxies must be obtained. Unfortunately, the Local Group of galaxies, which necessarily acts as the only available nearby sample of galaxies is noticeably deficient in two areas:

There are no massive elliptical galaxies

There is only 1 large spiral galaxy (M31)

Most of the Local Group galaxies are low mass, dwarf galaxies whose heterogeneous properties do not lend themselves as distance indicators. Figure 2-5 shows images of the Local Group dwarf irregular galaxies IC 1613 and NGC 6822.

Figure 2-5: Images of the Local Group Irregular galaxies IC 1613 and NGC 6822. Both galaxies are forming stars and hence have a small population of Cepheids. Both have some population II and also have RR Lyraes. Thus, these two galaxies can serve as consistency checks on the RR Lyrae/Cepheid distance scale, as discussed in the text. The Image on the left is a blue band CCD image of IC 1613 taken by the author. The image on the right is a color photograph of NGC 6822 taken by David Malin with the AAT telescope and reprinted with permission.

Because of the large number of empirical observations of its Cepheid and RR Lyrae content, obtaining an accurate distance to the LMC is absolutely crucial. In principle, this distance could define the zeropoint of both the Cepheid PL relation and the RR absolute magnitudes. When measuring the distance to the LMC there are two important sources of systematic uncertainty:

Foreground reddening: The reddening along the line of site to the LMC is not well known. This is primarily because the reddening is low and hence difficulty to accurately measure. The canonical value is E(B - V) = 0.07 (or A_V 0.23). But values of E(B - V) = 0.11 up to E(B - V) = 0.18 (Walker 1991) have been advocated for certain lines of sight. While the value of E(B - V) = 0.18 seems excessive, values in the range 0.06 E(B - V) 0.11 are consistent with the data. This translates directly into an 0.17 mag range for A_v which is 8% in distance. Hence, from this limitation alone, it does not seem possible to derive a distance to the LMC which is more accurate than 10%.

Depth effects: The true orientation of the LMC is not known and indeed is quite confusing. This can be seen by directly comparing R-band and H images of the LMC (reproduced in Figures 2-6 and 2-7) and noting the different appearance of the LMC. The bar area is highly flattened and has an axial ratio of 0.25. The main body of the LMC (area surrounding the bar) has an axial ratio of 0.70 ± 0.03, corresponding to an inclination to the line of sight of 48°. Including the detached 30 Doradus and Constellation III areas, however, raises the axial ratio considerably and lowers the derived inclination to 27°. Hence, the front-to-back distance of the physical structure that defines the LMC is not well known but maybe as large as 10% (e.g., 5 kpc) of its distance from the Milky Way.

Figure 2-6: Unique CCD Red-band image of the Large Magellanic Cloud. The image was taken with a Parking Lot Camera arrangement (described in Bothun and Thompson 1988) and the image scale is 36 arcseconds per pixel. The LMC is the major galaxy on which the Cepheid distance to the Virgo cluster is based.

Figure 2-7: Another CCD image of the LMC this time taken through a narrow band filter that highlights the emission from H II regions. Note how different the appearance of the LMC is in this image, compared to the R-band image of Figure 2-6.

In the following discussion all measurements have been placed on a reddening scale of E(B - V) = 0.07. Distances to the LMC determined from Cepheids show remarkable agreement. Such distances, however, are based on calibration using Cepheids in open clusters in the Galaxy, whose distances have been determined by main sequence fitting using either the Hyades or Pleiades fiducial sequences. Hence, some small systematic error could be present. The various distance moduli which have been obtained are 18.52 from BVI photometry (Feast 1988), 18.52 from JHK photometry (Laney and Stoble 1988), 18.50 from I-band photometry (Madore and Freedman 1991), and 18.42 from 1.05 µ photometry (Visvanathan 1991). Although the numbers of stars in these samples are relatively small (22 in the I-band sample), the agreement is very good. Moreover, there is good agreement between the optical and IR measurements, indicating that our adopted foreground reddening value is sensible. Madore and Freedman (1991) use multi-color photometry toward each Cepheid to determine the reddening. This, of course, has the advantage that both the foreground reddening of the Galaxy and the internal reddening of the LMC are determined (though not in a separable manner). There is very little evidence to date for either significant amounts of internal reddening or variations in internal reddening for the LMC. Modal averaging these distance estimates yields a distance modulus to the LMC of 18.50.

RR Lyrae derived distances, however are not completely consistent with the Cepheid distances. Walker (1992) presents comprehensive measurements of RR Lyrae stars in 7 LMC clusters. Excluding NGC 1841 which has a large reddening, the average V magnitude is 18.97 ± 0.03 at a mean metallicity of [Fe/H] = -1.9. At this value of [Fe/H], equation 5 yields M_V = 0.73 and hence (m - M) = 18.24, which is in conflict with the Cepheid value of 18.50. If we use the alternative calibration given in equation 5a the distance is increased by +0.36 in (m - M) to 18.60. If we use the alternative metallicity independent calibration (equation 6) then the distance modulus increases to 18.36. If we, instead, believe that the Cepheid calibration is correct and hence solve for the zeropoint in equation 5 using the mean V-magnitude of 18.97 for the RR Lyrae sample we derive a zeropoint of 0.76, or 0.25 magnitude brighter. Finally, if we assume that equation 5 is the correct calibration then a distance modulus of 18.50 can be recovered from the RR Lyrae data if we assume E(B - V) = 0.0.

On the theme of going where the data leads, we conclude that the Galactic calibration of the Cepheid and RR Lyrae distance scales can not be simultaneously correct. Indeed, the LMC is not the only Local Group galaxy to exhibit significantly different distance moduli between Cepheids and RR Lyraes. The same magnitude of difference is seen in the case of IC 1613 where the Cepheids give (m - M) = 24.42 (Freedman 1988) and the RR Lyraes give (m - M) = 24.10 (Saha et al. 1992). The discrepancy between these two distance measuring techniques has been explored in more detail by van den Bergh (1995) who eventually decides that the zeropoint discrepancy indeed remains unresolvable. However, van den Bergh (1995) points out that most of the evidence favors Equation 5 as the correct calibration in that 1) it can be theoretically reproduced using horizontal branch models (Dorman 1992), and 2) for a typical Galactic RR Lyrae ([Fe/H] -1.5) equation 5 predicts M_V = +0.78 which is excellent agreement with the statistical parallax value of M_V = +0.76 ± 0.14 derived by Hawley et al. (1985). Equation 5a, on the other hand, suggests M_V = +0.49 for a typical Galactic RR Lyrae star which is significantly brighter than actually observed.

A possible way to resolve the RR Lyrae-Cepheid disagreement on the distance to the LMC is to find another set of distance indicators that agree either with the Cepheid or the RR Lyrae-distance. Unfortunately, these other distance determinations to the LMC give yet different values. Some of these are distance determination techniques are the following:

Classical novae in our Galaxy show a relation between maximum amplitude and the rate of luminosity decline. As most of these novae are located in young clusters in the Galactic disk, the calibration of their intrinsic luminosities suffers from the same problems that plague the calibration of the Galactic Cepheid PL relation. Hence, the Galactic calibration of nova intrinsic luminosity is somewhat uncertain. This is clearly seen in that application of the nova method to the LMC by Capaccioli et al. (1990) yields (m - M) = 18.71 ± 0.30.

Certain long period variables, known as Miras, can also serve as standard candles, particularly in the infrared. K-band photometry of long-period variable stars by Hughes and Wood (1990) yield (m - M) = 18.64 ± 0.05. This distance rests on the Galactic distance to the globular cluster 47 Tucane which contains these kinds of stars. Hence, this is a Population II distance indicator.

As will be discussed later, the luminosity of planetary nebulae can be used as a distance indicator. Measurements of the mean magnitude of planetary nebulae detected in the LMC by Ciardullo and Jacoby (1992) yield (m - M) = 18.44 ± 0.18. This distance,however, is calibrated against the luminosity function of planetary nebulae in M31 and hence requires knowing the distance to M31 and we haven't gotten there yet.

In 1984 Schommer et al. made a bold attempt to determine direct distances to LMC clusters via the technique of main-sequence fitting. Using CCD photometry, Schommer et al. were able to track the main-sequence down to an apparent magnitude of v 23 (M_V +4.5) in 3 intermediate age LMC clusters. Fits to these intermediate age clusters initially produced values of (m - M) = 18.2, which are consistent with the Galactic RR Lyrae calibration but then inconsistent with the Galactic Cepheid calibration. Although the measurements were difficult, the fitting procedure was sound, provided that the theoretical Zero Age Main Sequence (ZAMS) for young stars of the metallicity was sound. Adjustments in that scale by Vandenberg and Poll (1989) showed that the previous ZAMS was too bright by 0.15 mag, thus adjusting (m - M) upwards to 18.35 ( ± 0.15).

Finally, distance determinations to the LMC received a serendipitous boost due to Supernova 1987a (Figure 2-8). Analysis of its expanding photosphere (Eastman and Kirshner 1989) and its light echo as manifested by the circumstellar ring (Panagia et al. 1991) both yield (m - M) = 18.50 ± 0.15. But these results are model dependent and different models can give slight different results (see Gould 1994b). Indeed, a recent re-analysis of the ring data by Gould (1995) gives a distance to SN 1987a of (m - M) = 18.37 ± 0.04.

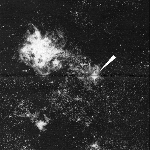
Figure 2-8: CCD image showing the immediate environment of Supernova 1987A shortly after it occurred in the LMC. Geometrical models and expansion velocities can be used to estimate a distance to this Supernova (see Gould 1995).

Based on all these data, we feel the true distance modulus to the LMC lies in the range 18.35 - 18.55 and that, within this range, there is no resolution towards any particular value. There certainly doesn't seem to be any best one distance indicator to the LMC. For instance, the measurements which are least sensitive to uncertainties in foreground reddening are the H-band observations of Cepheids which give (m - M) = 18.5 and the ring data which gives (m - M)= 18.35. It seems unlikely that depth effects have conspired to produce this range in distances (e.g., Supernova 1987A is on the very near side of the LMC). Finally, the metallicity-dependent galactic calibration of the RR Lyrae stars gives (m - M) = 18.25 based on equation 5 or (m - M) = 18.60 based on equation 5a. Hence, uncertainty in the distance to the LMC remains one of the larger sources of systematic uncertainty in the determination of H₀.

The Andromeda Galaxy - M31

M31 is the only large spiral in the local group and hence is a fundamental calibration point for virtually all extragalactic distance indicators that are applicable beyond 5 Mpc. There have been several recent determinations of distances to M31 and, in general, these indicators show convergence to a specific value. However, most of these distance estimates depend on knowing what the distance to the LMC is. In addition, M31 has an inclination of 80° and hence internal reddening variations across its disk are important. The most recent and credible determinations of the distance to M31, assuming that the total V-band absorption to M31 (foreground reddening + M31 average internal extinction) is 0.4 mag, are the following:

Welch et al. (1986) measured H-band magnitudes of 7 Cepheids and obtained (using 18.45 for the LMC modulus) (m - M) = 24.26 ± 0.16. While these observations have the advantage of being mostly unaffected by reddening, the Cepheids themselves are rather faint at H-band. Moreover, the observations were not done with an imaging detector, but rather done with a single-channel photometer. Imaging observations are preferred as a more precise value of local sky can be determined from them and they are freer from the crowding problems that can strongly affect single-channel aperture photometry.

Freedman et al. (1990) measure BVRI magnitudes of a few Cepheids and obtained (m - M) = 24.38 ± 0.13. The difference with the H-band data may be due to an underestimate of the internal reddening in M31 or systematic errors in the H-band magnitudes. In any event, the difference is small and within the respective error bars.

M31 has some bright, extended globular clusters. Color-Magnitude diagrams of stars in those clusters can reveal, with some noise, the giant branch. In principle, this giant branch can be fit to the giant branches of similar Galactic Globular Clusters of "known" distance. Christian and Heasley (1991) obtain (m - M) 24.3 with this method, though the errors are somewhat large and difficult to properly estimate.

A similar procedure was done by Mould and Kristian (1986) who fit metal-poor giant branches to Red Giants measured in the halo of M31. This has the advantage that the Halo fields are relatively unreddened. They obtain (m - M) = 24.23 ± 0.15 but this calibration rests on distances to Galactic globular clusters.

RR Lyrae stars have been detected and measured in the halo of M31 by Pritchet and van den Bergh (1987) with a resultant modulus of (m - M) = 24.33 ± 0.15. This assumes M_V = +0.6 for RR Lyraes.

Two other indicators are available: Novae (Capaccioli et al. 1989) give (m - M) = 24.27 ± 0.20 and Carbon stars, again using the LMC as the calibrator, give (m - M) = 24.45 ± 0.18 (Richer et al. 1990).

In general, all these distance indicators yield a pretty uniform set of distances to M31 but all of them, except for Novae and RR Lyraes, depend upon the distance to the LMC. For an LMC modulus of 18.45, the most probably distance modulus to M31 is in the range 24.25 - 24.40. In the case of M31, there is very good agreement between the Cepheid and RR Lyrae Distance scales. This further strengthens the case for a slightly different zeropoint for the RR Lyraes in the LMC compared to the Galaxy and M31 which indicates that the dependence of absolute magnitude on metallicity for RR Lyraes is still not understood.

The Other Spiral - M33

The last local group calibrator of the extragalactic distance scale is M33 (see Figure 2-8). M33 has an inclination of 57° and hence internal reddening problems are not as severe as in the case of M31. We use a reddening of E(B - V) = 0.07 (see van den Bergh 1991) and adjust all quoted distances below to this reddening value. Techniques similar to those used to obtain the distance to M31 have been applied to M33 and assume the same distance modulus to the LMC. Notably, M33 also shows a discrepancy in distance determinations between the Population I indicators and the Population II ones. We begin with the Population I distance scale:

H-band photometry of a handful of Cepheids, again obtained using a single-channel aperture device, yield (m - M) = 24.20 ± 0.14 (Madore et al. 1985); a distance actually less than the distance of M31. In contrast, BVRI photometry by Freedman et al. (1991) yields (m - M) = 24.58 ± 0.13. It seems unlikely that this discrepancy is the result of underestimates of the reddening in the Freedman et al. sample and hence likely reflects systematic errors in the H-band photometry of faint Cepheids. We emphasize that, since the H-band sky background is 14.0 mag arc sec^-2 , accurate determinations of H-band magnitudes of stars as faint as h = 19.0 requires a very accurate determination of the sky background. This is non-trivial with a single aperture as the detector. Ultimately, JHK imaging observations of Cepheids in M33 will be required to sort out the discrepancy noted above.

Mould et al. (1990) used photometry of Long Period variables in M33 in comparison with those in our Galaxy to derive (m - M) = 24.52 ± 0.17.

Studies of the rates of decline of classical Novae in M33 give (m - M) = 24.38 ± 0.20 (Della Valle 1988)

An average of these 4 population I indicators gives a distance to M33 of (m - M) = 24.42 ± 0.17. Removal of the suspect H-band observations from this aggregate yields (m - M) = 24.49 ± 0.10 which we adopt as the Population I distance scale to M33.

The Population II distance indicators are the following:

Again assuming M_V = +0.6 for RR Lyrae stars, the observations of Pritchet (1988) yields 24.60 ± 0.23. This distance is only discrepant by 0.1 mag with respect to the Population I result. The real problem lies in the determination made by Mould and Kristian (1986) using the halo giant branch of M33. Recall that the same procedure applied to M31 gave results quite consistent with the Cepheid scale. In the case of M33, Mould and Kristian derive (m - M) = 24.80 ± 0.3. Analysis of another sample of halo red giants by Wilson et al. (1992) yields (m - M) = 24.60 ± 0.3. The relatively large error bars on these measurements are an accurate indicator of the difficulty of this distance determination method as 1) accurate photometry of the halo stars must be done, 2) very good background subtraction must be done in order to properly isolate the Halo giant branch in the CM diagram of the general field, 3) there must be a good calibrating giant branch available for a globular cluster in our Galaxy. Since the Halo of M33 is quite sparsely populated, an extra degree of difficulty comes into play compared to M31. Taking the average of these three indicators (there is nothing in the data that suggests the MK result is any less valid than the Wilson et al. result) yields (m - M) = 24.67 ± 0.11 as the Population II distance scale to M33. This is consistent with a recent review by van den Bergh (1995) who derives gives (m - M) = 24.67 ± 0.07 for the Population II distance to M33. This error bar is unrealistically low and gives the erroneous implication that the Pop II scale is more precisely determined than the Pop I scale.

We regard the distance to M33 as unresolved but note that if we just take the Cepheid BVRI data and the RR Lyrae data, then a consistent distance of (m - M) = 24.6 results. This would imply that the Galactic zeropoint of both the Cepheid and RR Lyrae scales are good - in sharp contrast with what is found in the LMC. On the basis of all the data, we would place M33 at a distance of (m - M) = 24.4 - 24.8 with a prejudice towards a probable value of 24.6.