3.6.4. Infall Around the Great Attractor: A Case Study
Virialized structures in the Universe produce velocity perturbations of
galaxies which are located near them. The amplitude of these perturbations
(
v / v) depends on the
background density of the Universe
(
)
and the density contrast
(
/ ) interior to the shell upon
which the galaxy is located. The unperturbed velocity in this
case is given by v = H0r where r is the
distance from the source which is causing the perturbation.
The only situation which can be solved
analytically (e.g., Regos and Geller 1989, Lightman and Schechter 1990)
is the case of a spherical density perturbation in which case
v / v
can be expanded in powers of / as:
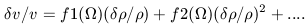
| (37) |
In the linear approximation of Peebles (1980), equation 37 is usually abbreviated to the form
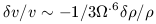
| (38) |
More precise derivations by Regos and Geller (1989) and Lightman and S
Schechter (1990)
yield values of f1 = -1/3
.57 and f2 = 4/63
.62. This
second order approximation, as well as the fifth order approximation of
Regos and Geller, are only valid in the regime of small
/ . For
denser regions it is necessary to employ the exact solution of Regos and Geller
(1989).
However, Regos and Geller do note that
the non-linear approximation of Yahil (1985) tracks the exact solution
quite well out to overdensities of
20. That approximation is of
the form
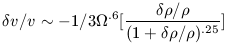
| (39) |
Equation 39 is the standard infall equation that can be used to predict
peculiar velocities as a function of radial distance from a virialized
structure. To make a prediction a value for
has to be assumed
and the radial fall off with distance from the center of the virialized
structure of / must be estimated. In
general, one assumes
that that / falls of
as r
, where gamma is
taken to be 2. We can also define the
the turnaround radius (rt) of a virialized structure as the radius
at which the inward peculiar velocity of a shell
exactly cancels its outward expansion as seen by the center of the
virialized structure. This condition requires
v / v = -1.0. In an
=1.0 universe,
the mean density enclosed within rt is 5.5 (assuming
spherical symmetry)
, or / = 4.5. Equation 39
predicts v / v = -1 at
/ = 4.67. The density
contrast within rt as a function of
is given by Regos
and Geller (1989). In an = 0.1
universe, the density contrast
is 29 and hence even the non-linear approximation breaks down
before rt is reached. In that sense, infall patterns are easier to
treat in the case of = 1.0 as
non-linear effects do not quite
set in so rapidly.
We now have a framework for analyzing peculiar velocities in terms
of a spherical infall model. In principle, such analysis can also
determine or constrain . More
stringently, the analysis really only constrains
.6 / b, where b is
the bias parameter
used in linear biasing theory. If on the scale of
the observations, mass is a perfect tracer of light then b =1 and
can be recovered
directly. Studies of peculiar velocities
for galaxies in the vicinity of the Hydra-Cen supercluster, however,
convincingly show that this procedure is not very straightforward.
As such, the history of these studies is an excellent case study
of the complex and ambiguous nature of the peculiar velocity field
which makes the overall pattern difficult to decipher.
The Hydra-Cen supercluster consists of two main mass concentrations,
the Hydra Cluster and the Centaurus cluster. They are denoted by
the letters C and H in
Figure 3-8 where it is seen
that Centaurus
is a part of the Super-Galactic plane. The Hydra cluster appears
to be unperturbed and is at rest with respect to the CMB with a
cosmic velocity of 4055 km s-1. On the other hand, the
velocity histogram of Centaurus is strongly bi-modal
with one peak occurring at v
3000 km s-1 (Cen30) and the other at v
4500 km s-1 (Cen45).
Using a sample of elliptical galaxies,
Faber et al. (1989) report kinematic distances
of 2220 ± 250 km s-1 for Cen30 and 3175 ± 335 km
s-1 for Cen45.
These distances are substantially less than their redshift distances which
indicates that Cen30 and Cen45 both have positive peculiar
velocities. In conflict with this result are the observations of
Lucey and Carter (1988) who measure kinematic distances for a
similar sample of elliptical galaxies to determine peculiar
velocities of 3115 ± 280
km s-1 for Cen30 and 2675 ± 435 km s-1 for
Cen45. These results indicate
that Cen30 is at rest and Cen45 is infalling at v
2000 km s-1. The
opposite case was
found from an analysis of the relative distances to spiral galaxies.
Using the TF relation, Aaronson et al. (1989) derived mean peculiar velocities
of 2835 ± 250 km s-1 for Cen30 and 4260 ± 450 km
s-1.
In this case, Cen30 exhibits a
600 km s-1
velocity residual, while Cen45 would appear to be at rest.
Clearly, there is widespread disagreement among the various datasets.
The basis of the GA driven inflow model of Lynden-Bell et al. (1988) is that
both Cen 30 and Cen 45 have peculiar velocities with amplitudes of
1100 km s-1. If the observed DA of 600 km s-1 for
the Milky Way is also
the result of GA driven inflow, then we have two values of
v / v
at two different distances. With some assumptions, these data can be
input to equation 39 to fix the distance of the GA.
A GA driven acceleration of the LG with an amplitude of 600 km s-1
requires rt 13 Mpc or a
mass 20 times that of the
Virgo cluster. For
= 1.0 this
corresponds to a mass of 1.3 x 1016
M
within r = 13
Mpc. Lynden-Bell et al. (1988) derive a mass of
2.7 x 1016
M within r = 44 Mpc.
For = 0.1 the enclosed mass is
reduced by a factor of
3. For the smaller scale case of the
Virgo cluster, a LG infall velocity of 250 km
s-1 requires
the Virgo cluster
to have a turnaround radius of 4.5-5 Mpc.
As of 1991, there were are two alternatives to the GA driven inflow
model which remained
consistent with the data. 1) Cen30 is at rest (at v
3000 km s-1) and
drives an acceleration of the Local Supercluster towards it. This
is what was schematically shown in
Figure 3-17.
2) Cen30 has
the same peculiar velocity (e.g., 600 km s-1) as the Milky
Way and is hence
participating in the same flow pattern. The simultaneous existence
of three very different physical models to the same data set illustrate
how ambiguous this problem is. However, a GA driven infall model
should be symmetric on both the front and back sides and, as of 1991,
only data existed on the front side. The discovery of infall on the backside
of the GA would therefore confirm that model.
In 1992 and 1993 the Aaronson et al. group (see Bothun et al. 1992; Mould
et al. 1993) published two papers which definitively showed that there was
no backside infall towards the hypothesized GA. Other investigators
soon reached similar conclusions (e.g., Mathewson et al. 1992).
Figure 3-18 summarizes the situation as
it presents a comparison of the model infall pattern (equation 39)
with the data of Bothun et al. (1992).
The GA center distance has been set to be 4350 km s-1,
the value proposed by Lynden-Bell et al. (1988). The dashed vertical
lines define rt. Points outside of rt are expected
to fall-off
along the solid lines, which represent the imaginary caustic surface
of the virialized structure. The model does not go to 0 at r = 43.5 because
we have normalized the model to a value of 600 km s-1 at that
distance as we assume the DA is generated by the GA.
The dotted lines around the model show the effects of distance errors on
the quantity v / v.
|
Figure 3-18: Individual galaxy peculiar velocities plotted in comparison with the spherically symmetric infall model that would be generated by a Great Attractor located at kinematic distance of 4350 km/s from the Milky Way. The solid curved lines define the front-side and back-side caustic infall surfaces and the dashed lines represent 1-sigma error surfaces. The solid vertical lines represent rt for the Great Attractor. The letter A denotes the Antlia cluster. The model has been normalized such that the Great Attractor accounts for the entire observed dipole anisotropy in the CMB. Figure adapted from Figure 4 in Bothun et al. (1992a). |
If infall towards the GA center is responsible for producing the
observed amplitude of LG acceleration we would expect the observed
data points to fall within the error surfaces surrounding the basic
infall model.
It is obvious that on the near side the data are generally at much higher
peculiar velocity than the model would predict. On the backside, while
some points fall within the model predictions many do not and many have
the wrong sign for the observed peculiar velocity. To better examine the
data set, it is convenient to break it up into three samples
which we denote as F (far), N (near), and T (transverse). Sample F
is located at a mean distance of 35 Mpc on the backside
of the GA center. At this distance, the model predicts Vp =
-705 ± 40 km s-1. The data yield Vp =
-717 ± 462 km s-1 which
is a 1.5 
detection of backside infall which we do not consider significant.
Sample N is located at a mean distance of 21.5 Mpc from the GA on the
near side. The model predicts Vp = +1006 ± 30 km
s-1 but the data
yield Vp = +2366 ± 334 km s-1. Hence,
the F and N samples do not indicate any of the required symmetry associated
with an infall pattern driven by a virialized structure. Finally,
there is the sample T galaxies. These are galaxies whose radial infall
to the GA is perpendicular to our line of sight and hence
Vp should
be zero. However, the measured Vp for this sample is
851 ± 181 km s-1.
Thus, the
transverse sample does have a significant radial component to its peculiar
velocity when, in fact, none should have been observed in the context of
symmetric spherical infall towards the GA center.
On balance, the available data seem to rule out the GA model as a viable
one that explains the local peculiar velocity field. By itself, the GA model
was always worrisome as one could not optically identify a large concentration
of light that would correspond to the GA. While the GA is at somewhat
low galactic latitude, it sufficiently big in angular extent that obscuration
by our own galaxy shouldn't prevent its detection in a redshift survey.
At the GA center distance of 4350 km s-1, rt subtends an
angle of 16.5°.
Figure 3-19 shows the redshift cone diagram in
the proposed GA direction for all galaxies with redshifts
that are located within the projected turnaround radius of the GA. The
very obvious virialized finger belongs to the Centaurus cluster, a structure
that was originally measured to have
Vp 1100 km
s-1 and provides the foundation of the GA model. In
Figure 3-19 the GA center is located
at (0,4350). There is no hint of any virialized structure at this
location. Since spherical infall is
best generated by virialized structures, the Centaurus cluster is an
excellent candidate for contributing to the observed CMB DA. It is
hence difficult to understand the observations which suggest that
the Centaurus cluster moves in the same 600 km
s-1 flow as the LG does.
|
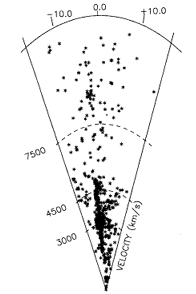
Figure 3-19: Cone diagram for all known velocities that are in the putative Great Attractor region of the sky. The large "finger" which is seen is the Centaurus cluster. |
To date, the situation with respect to the origin, scale and
evolution of peculiar velocities remains confusing. The acquisition of
more data
by Mould et al. (1993,1995) suggests a picture that is hybrid between
that obtained by Aaronson et al. (1986) and the
Dn- group.
In this scenario, the Hubble flow as delineated by nearby clusters of
galaxies is relatively quiet except for samples in the vicinity of
large superclusters such as Hydra-Cen or Perseus-Pisces. At these locations,
substantial large scale flows are seen with up to 50% of the observed
velocity being due to peculiar motions.
Figure 3-20 presents a representation of the
flow pattern as it has been
measured for nearby clusters of galaxies. This flow pattern remains
consistent with either bulk flow models or infall driven models
with no clear resolution in sight (see also Strauss and Willick 1995).
|
Figure 3-20: Distribution of known peculiar velocities for nearby groups and clusters as projected on the plane of the Local Supercluster. Nominal distances are in km/s and the amplitude and direction of any measured peculiar velocity is indicated by the arrows that are tagged onto some groups and clusters. Figure adapted from Mould et al. (1993). |