5.3.3. Beyond CDM: More Exotic Scenarios

For completeness, we discuss four other fairly non-standard structure formation scenarios that complement, and or dominant, over the gravitational instability paradigm.

Primordial Baryon Isocurvature Model (PBI): This model from Peebles (1987) is quite elegant in its simplicity and directly relates to what we presently observe in the Universe. The model is an evolution of work done in the early 70's when the cosmological parameters H₀ and were thought to be known accurately. In the PBI model, the universe consists of photons, baryons, and three species of massless neutrinos and hence is strictly baryon dominated. Initial density perturbations take the form of entropy perturbations which are fluctuations in the baryon-photon and/or baryon-neutrino number densities. Since there is no obvious mechanism to generate these entropy perturbations, they are assumed to take the form of a power law. The index, n, of the power law is inferred from present day observations and hence the observed n 1 case is perfectly consistent with PBI. Since baryons are strongly coupled to photons in the early universe, there will be some scale over which photon diffusion erases the perturbation. Below this scale, the initial entropy fluctuations become the density perturbations that seed large-scale structure. As density perturbations above this scale can not form, the slope of the power spectrum rises significantly and becomes quite steep ( n + 4) just below this scale. In this model, structure formation can rapidly occur right after recombination and dense perturbations could give rise to the formation of massive star clusters and/or QSOs which become significant sources of ionization for some time after recombination.

Topological Defects: This is a very complex theory whose origin is motivated by the physically reasonable proposition that as the very early Universe undergoes a phase transition, symmetry is spontaneously broken which gives rise to some kind of defect (e.g., a cosmic string, a domain wall, magnetic monopoles). The defect network then evolves and provides the seeds for structure formation. As the network constantly evolves (the defects can't "damp" out) density perturbations are constantly being produced in a manner that is not easily characterized by the normal random phase hypothesis that leads to Gaussian fields. Hence, evidence of any significant non-Gaussininity in the COBE temperature fluctuation data would be consistent with defect-driven structure formation models. The absence of this component, however, would likely rule out this model (see Bennet and Rhie 1993).

Explosions; When the first CFA SLICE results were presented and the cellular pattern in the galaxy distribution first became apparent, Jerry Ostriker and his co-workers at Princeton came up with a series of models that involve primordial explosions and subsequent hydrodynamic evolution of a network of expanding shells, due to the explosions, that sweep up the material. This model naturally evacuates large regions, leading to voids, and collects this material at the intersection of shells. Qualitatively, this agrees quite well with the observed galaxy distribution. These explosions occur after matter and radiation decouple and hence serve as a non-gravitational component to structure formation. While the source of the explosions are unknown, they can plausibly be associated with the energetics of galaxy formation and the release of energy via Supernova explosions. The kinetic energy carried by the supernova plows into the surrounding medium and pushes it into a shell of radius R_s. The physical parameters which determine this radius are the released kinetic energy, the timescale over which this energy is transported (if this is longer than the expansion timescale, there is no effect), and the density of the surrounding medium.

We can make an approximation that the time scale is essentially given by (G )^-1/2 which leaves us with only two parameters, the timescale and the kinetic energy, E. To yield units of length, the correct combination of these two parameters is:

where E can be identified with the energy from supernova explosions. For typical values of E associated with the formation of a large galaxy, R_s is in the range of a 1-5 Mpc which is comparable to the average separation between galaxies (Chapter 3). While the explosion scenarios is not likely to be correct in detail, it does offer two important points: 1) the formation of galaxies is likely to be affected by the process itself due to energy feedback (just like the formation of stars in giant molecular clouds is affected) and 2) it may be wise to consider the hydrodynamical evolution of density perturbations since we clearly live in a void filled universe. Further work by Cen and Ostriker (1994) clearly shows the relevance of hydrodynamics in structure formation scenarios.

Primordial Turbulence: This is a rather old theory whose details were worked out in the late 60's and early 70's by groups in Italy and the Soviet Union (e.g., Bonometto et al. 1974; Bonometto et al. 1975; Dallaport and Luchhin 1973; Ozernoi et al. 1968; Sunyaev 1970). By most accounts, it has been discarded or forgotten today. However, this theory contained the seeds of the hydrodynamic treatment in today's models and can be considered as a reasonable precursor to the explosion scenario. In this theory, structure formation is a consequence of the initial turbulence spectrum in the early Universe. Eddy viscosity serves as a significant source of damping for perturbations on small scale and virtually all proponents of this theory demonstrate that, in high Universes photon viscosity damps out galaxy size perturbations. Hence, when inflation appeared in 1980, there was no more room for this theory in the consideration of cosmological models. Now however, since we have no viable structure formation model, turbulence might as well re-emerge as a contender, In this theory, density fluctuations can be expressed as

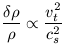
(33)

where v_t is the turbulent velocity and c_s prior to recombination is

(34)

where _r and _m are the radiation and matter densities. Hence, random motions in the turbulent fluid which are subsonic prior to recombination, become supersonic as _r decays. The subsequent shock waves associated with this supersonic turbulence act to compress matter into high density regions that condense out of the expanding background. The perturbation spectrum is set by the non-linear transfer of energy from large scales to small scales which is given by the familiar Kolmogorov spectrum

with the largest scale set by the condition that the hydrodynamical interaction timescale is equal to the expansion age of the Universe.

Silk and Ames (1972) postulated that the maximum turbulent velocities were 0.1c else too large of density fluctuations would occur and these would have collapsed into relatively dense structures at early epochs. Their treatment shows that the turbulent velocity decays fairly slowly. The rapid expansion of the horizon feeds the turbulence and allows density fluctuations to grow with time. The larger scale eddies then are dissipated by viscous decay prior to recombination. After recombination, supersonic turbulence then destroys any large scale surviving fluctuations. Silk and Ames (1972) contend that only small scale fluctuations can then survive. These grow into galaxies through conventional gravitational instability. In direct contrast to this model, Stein (1974) argued that turbulence is a natural mechanism for producing cluster-sized fluctuations instead of galaxy sized ones. Stein (1974) developed a rigorous criteria for eddies to damp out as a function of their turbulent velocity. The physical criteria is defined by the familiar Reynolds number of fluid dynamics. If the Reynolds number is on the order of unity before recombination then photon viscosity will completely erase the turbulence. The turbulent velocity is assumed to arise out of some primordial chaotic velocity (V_L).

Values of V_L / c 0.4( h²)^13/8 damp out. This conforms to other models which show that the initial turbulent velocity must be quite high (e.g., 0.4c) if turbulence is to survive until recombination. In general, large turbulent velocities are present in larger scale eddies. Stein (1974) shows that density fluctuations that arise from turbulent eddies with a mass of 10¹⁴ M have gravitational binding energy that exceeds the turbulent energy and hence are bound. This mass corresponds to that of a moderate cluster of galaxies. The predicted collapse redshift of these turbulence produced bound density perturbations is z = 1.3 - 10.5. Of course, such structures would be predicted to have substantial angular momentum and hence clusters should rotate. Since cluster velocity fields are complicated by the presence of substructure, or the quadrapole anisotropy introduced by surrounding clusters, net cluster rotation which is significantly less than the internal velocity dispersion would be difficult to detect.

Finally, in addition to being intrinsically non-linear, turbulence also has the advantage of naturally producing angular momentum in structure. In general, its difficult to account for the observed angular momentum in galaxies. In CDM and its variants, the angular momentum is thought to arise as a result of tidal-torques between neighboring proto-galaxies. However, observations show that the angular momentum of galaxies is independent of their environment.