6.2.1. The Luminosity Function of Galaxies

For most purposes, the GLF is assumed to have the functional representation first suggested by Schechter (1976):

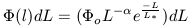
(9)

where (l) specifies the space density of galaxies over some luminosity interval dL. This function is schematically illustrated in Figure 6-3. There are three free parameters that must be observationally determined :

(0): This provides the overall normalization (at z = 0) of the GLF. An accurate measurement of (0) requires a fair, volume-limited sample of galaxies.

L_*: This is the normalization of the sharp exponential cutoff term in equation 6.9. Galaxies with luminosity in excess of L_* have quite low space density. There have even been attempts (e.g., Trevese et al. 1996; Oegerle and Hoessel 1989; Gudehus 1989; ) to construct the extragalactic distance scale by assuming that L_* is universal and independent of environment. Observations of clusters of galaxies which reveal L_* can be used to obtain relative cluster distances. As we remark below, we do not yet have a secure determination of the overall GLF and hence using its "features" to determine extragalactic distances is likely to contain unknown systematic errors. However, it is true that most studies of nearby redshift samples yield approximately the same value for L_*. For H₀ = 100, this value is 10¹⁰ blue L .

: This is the faint end slope of the GLF. Of the three free parameters, this has the most cosmological significance as it determines the amount of mass that can potentially be locked up in low luminosity/low mass galaxies. For many years was thought to have a slope of 1.25 for field galaxies and 1-1.1 for galaxies which were members of clusters. However, in the last 2-3 years a series of observations have challenged this value and suggest a considerably steeper faint end slope.

Figure 6-3: Top panel: Schematic representation of the Schechter formulation that describes the galaxy luminosity function. This function is defined by a characteristic luminosity, L*, and normalized space density at that luminosity, N*, along with the slope of the faint end. The solid line indicates a relatively flat faint end slope, that represents what is usually obtained in samples that are not corrected for surface brightness selection effects. The dashed line shows the case of a steep faint end slope in which most of the galaxies in the Universe are faint/low mass objects. Bottom panel: Examples of various luminosity functions that have been obtained. The dashed line comes from the Marzke etal (1994a) data for all morphological types in the CFA redshift survey while the dotted line is the case for only low luminosity irregular galaxies in that survey. Note that the faint end slope is significantly stepper for that subset. The solid line is a maximum likelihood fit to the data for field LSB galaxies. That relation shows a fairly steep faint end slope as well. Data and figure are from Sprayberry et al. (1997).

The universality of the free parameters of the GLF have come under fire primarily because the GLF seems to be a function of morphological type. In their detailed study of the Virgo Cluster, Sandage and Tammann (1985) were able to convincingly demonstrate that the GLF for spiral galaxies was better fit by a Gaussian than the Schechter function. This actually had been known years earlier by H I observers as plotting the distribution of rotation velocities in spiral galaxies, which are correlated with galaxy luminosity through the Tully-Fisher relation, generally yielded a Gaussian distribution. (see an example in Figure 6-4). A detailed study of the CFA redshift survey by Marzke et al. (1994) has produced the important result that the faint end slope, , also seems to depend on morphological type. For low mass irregular galaxies, Marzke et al. (1994) find a rather steep slope of = -1.9, close to the maximum allowable slope of -2.0 (where the integral over the GLF becomes divergent). Further modifications of the GLF have occurred as a result of the discovery of LSB galaxies which we will discuss shortly.