Annu. Rev. Astron. Astrophys. 1992. 30: 359-89 Copyright © 1992 by Annual Reviews. All rights reserved

2.4 Absolute Magnitudes

In this section we discuss only the uniformity of the absolute magnitudes, and defer the calibration to Section 3. We first discuss the absolute magnitude scatter without making any allowance for extinction in the parent galaxies.

In a Hubble diagram for SNe Ia, i.e. in a plot of log v₀ versus apparent magnitude, the scatter is due not only to intrinsic scatter in absolute magnitude but also to peculiar motions, to extinction in the parent galaxy, and to observational magnitude errors, Tammann & Leibundgut (1990) have considered a sample of 35 SNe Ia with reasonably well determined apparent magnitudes in galaxies with recession velocities larger than v₂₂₀ = 1000 km s^-1. (The v₂₂₀ values are corrected for a self-consistent Virgocentric velocity model having an infall velocity at the Local Group of 220 km s^-1.) The velocity limit is imposed to guard against strong influences of peculiar motions. The observed magnitude scatter about the Hubble line is _B = 0.53 mag. With reasonable assumptions about the influence of peculiar motions and observational errors, it was concluded that the true intrinsic scatter of the blue absolute magnitudes is less than _B = 0.25 mag.

Table 1. Galaxies with two SNe Ia

Galaxy	SN	mB0	mV0	(B - V)0	position	E (B - V)	AB	mB00	mV00
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
NGC 1316	1980N	12.49B	12.44V	0.05	outer	0.20	0.30	12.19	12.34
	1981D	12.59B	12.40V	0.19	inner	0.34	0.51	12.08	12.23
NGC 3913	1963J	13.1pg	12.5pv	0.6	inner	0.75	1.13	11.97	12.12
	1979B	12.5pg	12.4V	0.1	outer	0.25	0.38	12.12	12.27
NGC 4753	1965I	12.5B	12.7V	-0.2	outer	0	0	12.50	12.70
	1983G	13.1B	12.8V	0.3	inner	0.45	0.68	12.42	12.57
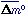	:	0.43	0.08					0.11	0.13

Another way to check the absolute magnitude scatter is provided by galaxies that have produced two confirmed SNe Ia. The few such galaxies and their supernovae are listed in Table 1. The maximum magnitudes are taken from Hamuy et al (1991) and LTCC91. With no allowance for differences in parent-galaxy extinction, the mean magnitude differences of 0.43 and 0.08 mag must be considered as upper limits.

A third way to estimate the absolute magnitude scatter is provided by the nonpeculiar events that have occurred in the Virgo cluster (Tammann 1988, Capaccioli et al 1990). Table 2 lists the six SNe Ia that have sufficiently well determined B maxima (from LTCC91) and have occurred in certain member galaxies of the Virgo cluster [for a discussion of membership see Binggeli et al (1985) and Leibundgut & Tammann (1990)]. As Table 2 shows, the scatter of maximum magnitudes is _B = 0.36 and 0.29 mag. Again, these values should be upper limits to the intrinsic scatter. It is worth noting that the least certain cluster member in Table 2 is NGC 4639, whose SN Ia was the faintest in the sample. A self-consistent Virgocentric model (Kraan-Korteweg 1985) allows the possibility that NGC 4639 (v₀ = 864 km s^-1) is at 1.25 times the Virgo distance, falling in from behind. If so, SN 1990N should be 0.48 mag fainter than the true Virgo SNe Ia, in agreement with observation. If NGC 4639 indeed is in the background, the scatter in Table 2 would be further reduced.

Table 2. SNe Ia in the Virgo Cluster

SN	Galaxy	mB0	mV0	(B - V)0	E (B - V)	AB	mB00	mV00
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
1957B*	N4374	11.7	11.8	-0.1	0.05	0.08	11.62	11.77
1960F	N4496	11.7
1961H*	N4564	12.0
1981B	N4536	12.0	12.0	0.0	0.15	0.23	11.77	11.92
1984A	N4419	12.45	12.30	0.15	0.30	0.45	12.00	12.15
1990N	N4639	12.65	12.57	0.08	0.23	0.35	12.30	12.45
	mean:	12.08	12.17				11.92	12.07
		0.36	0.29				0.26	0.26
* Assumed to be type Ia because occurred in E galaxy.

So far no corrections for parent-galaxy extinction have been applied, but there is reason and indeed good evidence that SNe Ia do suffer extinction in their parent (spiral) galaxies. Miller & Branch (1990, hereafter MB90) have shown that some SNe Ia in highly inclined spiral galaxies are exceptionally faint. They assume that the faint SNe Ia lie on the far side of the spiral and are strongly extinguished. After correcting these faint supernovae by A_B = 0.8 sec(i) mag, they find an absolute magnitude scatter of _B = 0.39 mag. Excluding five objects that occurred in Am (or I0) galaxies for which the extinction correction cannot be applied, they obtain _B = 0.27 mag, which can be entirely explained by apparent magnitude, distance, and Galactic extinction errors.

SNe Ia in spiral galaxies tend on the whole to be fainter and redder than their counterparts in elliptical galaxies, where the effect of extinction is expected to be smaller (Tammann 1982). This trend is confirmed by the data in Tables 1 and 2. Of the three pairs of SNe Ia that occurred in one galaxy, the fainter supernova always lies closer to the center of the galaxy and is redder (cf Table 1, columns 3-6). The SNe Ia in Virgo ellipticals are brighter by 0.35 mag than those in Virgo spirals, and there is a rather clear dependence between luminosity and color (Table 2, columns 3-5). The fact that the scatter is larger in B than in V (Table 1, columns 3 and 4, and Table 2, columns 3 and 4) also is characteristic of the effect of extinction.

To correct the data in Tables 1 and 2 for parent-galaxy extinction, the intrinsic color (B - V)⁰⁰ at maximum and the value of R are needed. (R_B = A_B / E_B-V and R_V = R_B - 1.) A value of (B - V)⁰⁰ = -0.15 has been adopted in Section 2.1. Arguments for a best, although unconventional, value of R^{B = 1.5 will be given in Section 2.5. With these choices the calculation of m_B00 and m_V00 in Tables 1 and 2 is straightforward. The resulting values of the magnitude scatter are _B = _V = 0.26 mag for the Virgo data, and for the small sample of SNe Ia pairs one finds a very low value of _{B V} = 0.12 mag!}

It is, of course, also appropriate to repeat the analysis of the SNe Ia Hubble diagram by including the extinction corrections. For this the (B - V)⁰ color at maximum is needed. These are available for only 14 (out of 35) SNe Ia. The inclusion of the extinction correction reduces the scatter about the Hubble line from _B = 0.53 to 0.38 mag (LT92).

The independent ways to estimate the scatter, after extinction corrections, give values of _{B V} = 0.12-0.39 mag. It must be stressed again that these values still contain effects of peculiar motions on the distances and the full observational errors of the magnitudes at maximum, which in most cases had to be interpolated or more frequently even extrapolated back in time by means of the adopted template light curves. In addition the adopted extinction corrections are anything but perfect.

From the above it appears unlikely that the true intrinsic luminosity scatter at B and V maxima could be larger than 0.25 mag. This makes SNe Ia the best standard candles known so far. If SNe Ia are such good standard candles at maximum light, and if, as argued in Section 2.1. they closely follow standard light and color curves, then they are standard candles at any given phase. This implies that their bolometric light curves are nearly identical and that their total energy output is the same to within 20%.