
GRAVITATIONAL THEORIES
Jacob D. Bekenstein
A theory of gravitation is a description of the long range forces that electrically neutral bodies exert on one another because of their matter content. Until the 1910s Sir Isaac Newton's law of universal gravitation, two particles attract each other with a central force proportional to the product of their masses and inversely proportional to the square of the distance between them, was accepted as the correct and complete theory of gravitation: The proportionality constant here is Newton's constant G = 6.67 x 10-8 dyn cm2 g-2, also called the gravitational constant. This theory is highly accurate in its predictions regarding everyday phenomena. However, high precision measurements of motions in the solar system and in binary pulsars, the structure of black holes, and the expansion of the universe can only be fully understood in terms of a relativistic theory of gravitation. Best known of these is Albert Einstein's general theory of relativity, which reduces to Newton's theory in a certain limit. Of the scores of rivals to general relativity formulated over the last half century, many have failed various experimental tests, but the verdict is not yet in on which extant relativistic gravitation theory is closest to the truth.
NEWTONIAN GRAVITATIONAL THEORY
In alternative language, newtonian gravitational theory states that
the acceleration a (the rate of change of the velocity v)
imparted by
gravitation on a test particle is determined by the gravitational
potential  ,
,
and the potential is determined by the surrounding mass distribution
This formulation is entirely equivalent to Newton's law of
gravitation. Because a test particle's acceleration depends only on
the potential generated by matter in the surroundings, the theory
respects the weak equivalence principle: the motion of a particle is
independent of its internal structure or composition. As the subject
of Galileo Galilei's apocryphal experiment at the tower of Pisa, this
principle is supported by a series of high precision experiments
culminating in those directed by Baron Lorand von Eötvos in Budapest
in 1922, Robert Dicke at Princeton in 1964, and Vladimir Braginsky in
Moscow in 1972.
Highly successful in everyday applications, newtonian gravitation
has also proved accurate in describing motions in the solar system
(except for tiny relativistic effects), the internal structure of
planets, the sun and other stars, orbits in binary and multiple
stellar systems, the structure of molecular clouds, and, in a rough
way, the structure of galaxies and clusters of galaxies (but see
below).
According to newtonian theory, gravitational effects propagate from
place to place instantaneously. With the advent of Einstein's special
theory of relativity in 1905, a theory uniting the concepts of space
and time into that of four dimensional flat space-time (named
Minkowski space-time after the mathematician Hermann Minkowski), a
problem became discernible with newtonian theory. According to special
relativity, which is the current guideline to the form of all physical
theory, the speed of light, c = 3 x 1010 cm
s-1, is the top speed allowed
to physical particles or forces: There can be no instantaneous
propagation. After a decade of search for new concepts to make
gravitational theory compatible with the spirit of special relativity,
Einstein came up with the theory of general relativity (1915), the
prototype of all modern gravitational theories. Its crucial
ingredient, involving a colossal intellectual jump, is the concept of
gravitation, not as a force, but as a manifestation of the curvature
of space-time, an idea first mentioned in rudimentary form by the
mathematician Ceorg Bernhard Riemann in 1854. In Einstein's hands
gravitation theory was thus transformed from a theory of forces into
the first dynamical theory of geometry, the geometry of four
dimensional curved space-time.
Why talk of curvature? One of Einstein's first predictions was the
gravitational redshift: As any wave, such as light, propagates away
from a gravitating mass, all frequencies in it are reduced by an
amount proportional to the change in gravitational potential
experienced by the wave. This redshift has been measured in the
laboratory, in solar observations, and by means of high precision
clocks flown in airplanes. However, imagine for a moment that general
relativity had not yet been invented, but the redshift has already
been measured. According to a simple argument owing to Alfred Schild,
wave propagation under stationary circumstances can display a redshift
only if the usual geometric relations implicit in Minkowski space-time
are violated: The space-time must be curved. The observations of the
redshift thus show that space-time must be curved in the vicinity of
masses, regardless of the precise form of the gravitational theory.
Einstein provided 10 equations relating the metric (a tensor with 10
independent components describing the geometry of space-time) to the
material energy momentum tensor (also composed of 10 components, one
of which corresponds to our previous
Despite the great contrast between General Relativity and Newtonian
theory, predictions of the former approach the latter for systems in
which velocities are small compared to c and gravitational potentials
are weak enough that they cannot cause larger velocities. This is why
we can discuss with newtonian theory the structure of the earth and
planets, stars and stellar clusters, and the gross features of motions
in the solar system without fear of error.
Einstein noted two other predictions of General Relativity. First,
light beams passing near a gravitating body must suffer a slight
deflection proportional to that body's mass. First verified by
observations of stellar images during the 1919 total solar eclipse,
this effect also causes deflection of quasar radio images by the sun,
is the likely cause of the phenomenon of ``double quasars'' with
identical redshift and of the recently discovered giant arcs in
clusters of galaxies (both probably effects of gravitational lensing),
and is part and parcel of the black hole phenomenon. In a closely
related effect first noted by Irwin Shapiro, radiation passing near a
gravitating body is delayed in its flight in proportion to the body's
mass, a time delay verified by means of radar waves deflected by the
sun on their way from Earth to Mercury and back.
The second effect is the precession of the periastron of a binary
system. According to newtonian gravitation, the orbit of each member
of a binary is a coplanar ellipse with orientation fixed in
space. General relativity predicts a slow rotation of the ellipse's
major axis in the plane of the orbit (precession of the
periastron). Originally verified in the motion of Mercury, the
precession has of late also been detected in the orbits of binary
pulsars.
All three effects mentioned depend on features of General Relativity
beyond the weak equivalence principle. Indeed, Einstein built into
general relativity the much more encompassing ``strong equivalence
principle'': the local forms of all nongravitational physical laws and
the numerical values of all dimensionless physical constants arc the
same in the presence of a gravitational field as in its absence. In
practice this implies that within any region in a gravitational field,
sufficiently small that space-time curvature may be ignored, all
physical laws, when expressed in terms of the space-time metric, have
the same forms as required by special relativity in terms of the
metric of Minkowski space-time. Thus in a small region in the
neighborhood of a black hole (the source of a strong gravitational
field) we would describe electromagnetism and optics with the same
Maxwell equations used in earthly laboratories where the gravitational
field is weak, and we would employ the laboratory values of the
electrical permittivity and magnetic susceptibility of the vacuum.
The strong equivalence principle effectively forces gravitational
theory to be General Relativity. Less well tested than the weak
version of the principle mentioned earlier, the strong version
requires Newton's constant expressed in atomic units to be the same
number everywhere, in strong or weak gravitational fields. Stressing
that there is very little experimental evidence bearing on this
assertion, Dicke and his student Carl Brans proposed in 1961 a
modification of general relativity akin to a theory considered earlier
by Pascual Jordan. In the Brans-Dicke theory the reciprocal of the
gravitational constant is itself a one-component field, the scalar
field
The Brans-Dicke theory also reduces to Newtonian theory for systems
with small velocities and weak potentials: It has a newtonian
limit. In fact, Brans-Dicke theory is distinguishable from general
relativity only by the value of its single dimensionless parameter
Initially a popular alternative to General Relativity, the
Brans-Dicke theory lost favor as it became clear that
However, constancy of
More than two score relativistic theories of gravitation have been
proposed. Some have no metric; others take the metric as fixed, not
dynamic. These have usually fared badly in light of experiment. Among
metric theories those involving a vector field or a tensor field
additional to the metric can display a preferred frame of reference or
spatial anisotropy effects (phenomena that depend on direction in
space). Both effects may contradict a variety of modern experiments.
Table 1 gives a sample of theories of
gravitation, summarizing the
main ingredients of each theory and its experimental status.
All relativistic gravitational theories mentioned so far have a
newtonian limit, a tacit requirement of candidate relativistic
gravitational theories until very recently. Now, if the correct
gravitational theory is general relativity or any of its traditional
imitations, then newtonian theory should satisfactorily describe
galaxies and clusters of galaxies, astrophysical systems involving
small velocities and weak potentials. But there is mounting
observational evidence that this can be the case only if galaxies and
clusters of galaxies are postulated to contain large amounts of dark
matter. Thus far this dark matter has not been detected independently
of the preceding argument.
Might not this missing mass puzzle signal instead the break-down of
the newtonian limit of gravitational theory for very large systems? In
this connection several schemes alternative to Newtonian theory have
been proposed. A well developed one is the modified newtonian dynamics
or MOND (see Table 1), in which the relation
between newtonian
potential and the resulting acceleration is regarded as departing from
newtonian form for gravitational fields with magnitude of
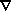
 ,
,
 by Poisson's partial differential equation
by Poisson's partial differential equation
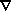 ·
·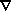
 = 4
= 4 G
G .
.
THE GENERAL THEORY OF RELATIVITY
 ). These Einstein field
equations, in which both of the previously mentioned constants G
and c
figure as parameters, replace Poisson's equation. Einstein also
replaced the newtonian law of motion by the statement that free test
particles move along geodesics, the shortest curves in the space-time
geometry. The influential gravitation theorist John Archibald Wheeler
has encapsulated general relativity in the aphorism ``curvature tells
matter how to move, and matter tells space-time how to curve.'' The
Eötvos-Dicke-Braginsky experiments demonstrate with high precision
that free test particles all travel along the same trajectories in
space-time, whereas the gravitational redshift shows (with more modest
precision) these universal trajectories to be identical with
geodesics.
). These Einstein field
equations, in which both of the previously mentioned constants G
and c
figure as parameters, replace Poisson's equation. Einstein also
replaced the newtonian law of motion by the statement that free test
particles move along geodesics, the shortest curves in the space-time
geometry. The influential gravitation theorist John Archibald Wheeler
has encapsulated general relativity in the aphorism ``curvature tells
matter how to move, and matter tells space-time how to curve.'' The
Eötvos-Dicke-Braginsky experiments demonstrate with high precision
that free test particles all travel along the same trajectories in
space-time, whereas the gravitational redshift shows (with more modest
precision) these universal trajectories to be identical with
geodesics.
SCALAR TENSOR THEORIES
 , that is generated by
matter in accordance with an additional
equation. Then
, that is generated by
matter in accordance with an additional
equation. Then  as well as
matter has a say in determining the metric
via a modified version of Einstein's equations. Because it involves
both metric and scalar fields, the Brans-Dicke theory is dubbed
scalar-tensor. Although not complying with the strong equivalence
principle, the theory does respect a milder version of it, the
Einstein equivalence principle, which asserts that only
nongravitational laws and dimensionless constants have their special
relativistic forms and values everywhere. Gravitation theorists call
theories obeying the Einstein equivalence principle metric theories.
as well as
matter has a say in determining the metric
via a modified version of Einstein's equations. Because it involves
both metric and scalar fields, the Brans-Dicke theory is dubbed
scalar-tensor. Although not complying with the strong equivalence
principle, the theory does respect a milder version of it, the
Einstein equivalence principle, which asserts that only
nongravitational laws and dimensionless constants have their special
relativistic forms and values everywhere. Gravitation theorists call
theories obeying the Einstein equivalence principle metric theories.
 which determines the effectiveness of matter in producing
which determines the effectiveness of matter in producing  . The
larger
. The
larger  , the closer the
Brans-Dicke theory predictions are to general
relativity. Both theories predict the same gravitational redshift
effect, although they predict slightly different light deflection and
periastron precession effects; the differences vanish in the limit of
infinite
, the closer the
Brans-Dicke theory predictions are to general
relativity. Both theories predict the same gravitational redshift
effect, although they predict slightly different light deflection and
periastron precession effects; the differences vanish in the limit of
infinite  . Measurements of
Mercury's perihelion precession, radar
flight time delay, and radio wave deflection by the sun indicate that
. Measurements of
Mercury's perihelion precession, radar
flight time delay, and radio wave deflection by the sun indicate that
 is at least several hundred.
is at least several hundred.
 must be very
large-an artificial requirement in some views. Nevertheless, the
theory has remained a paradigm for the introduction of scalar fields
into gravitational theory, and as such has enjoyed a renaissance in
connection with theories of higher dimensional space-time.
must be very
large-an artificial requirement in some views. Nevertheless, the
theory has remained a paradigm for the introduction of scalar fields
into gravitational theory, and as such has enjoyed a renaissance in
connection with theories of higher dimensional space-time.
 is
not conceptually required. In the generic
scalar-tensor theory studied by Peter Bergmann, Robert Wagoner, and
Kenneth Nordtvedt,
is
not conceptually required. In the generic
scalar-tensor theory studied by Peter Bergmann, Robert Wagoner, and
Kenneth Nordtvedt,  is
itself a general function of
is
itself a general function of  (
( ). It remains
true that in regions of space-time where
). It remains
true that in regions of space-time where  (
( ) is numerically large,
the theory's predictions approach those of general relativity. It is
even possible for
) is numerically large,
the theory's predictions approach those of general relativity. It is
even possible for  (
( ) to evolve
systematically in the favored
direction. Thus in the variable mass theory (VMT, see
Table 1), a
scalar-tensor theory devised to test the necessity for the strong
equivalence principle, the expansion of the universe forces evolution
of
) to evolve
systematically in the favored
direction. Thus in the variable mass theory (VMT, see
Table 1), a
scalar-tensor theory devised to test the necessity for the strong
equivalence principle, the expansion of the universe forces evolution
of  toward a particular value at
which
toward a particular value at
which  (
( ) diverges. Thus, late in
the history of the universe (and today is late), localized
gravitational systems are accurately described by general relativity
although the assumed gravitational theory is scalar-tensor.
) diverges. Thus, late in
the history of the universe (and today is late), localized
gravitational systems are accurately described by general relativity
although the assumed gravitational theory is scalar-tensor.
Theory
Metric
Other Fields
Free Elements
Status
Newtonian (1687)1
Nonmetric
Potential
None
Nonrelativistic theory
Nordstrom (1913)1,2
Minkowski
Scalar
None
Fails to predict observed light detection
Einstein's General Relativity (1915)1, 2
Dynamic
None
None
Viable
Belifante-Swihart (1957)2
Nonmetric
Tensor
K parameter
Contradicted by Dicke-Braginsky experiments
Brans-Dicke (1961)1-3 Generic Scalar
Dynamic
Scalar
 parameter
parameter
Viable for  > 500
> 500
Tensor (1970)2
Dynamic
Scalar
2 free functions
Viable
Ni (1970)1, 2
Minkowski
Tensor, Vector, and Scalar
One parameter,
3 functions
Predicts unobserved preferred-frame effects
Will-Nordtvedt (1972)2
Dynamic
Vector
None
Viable
Rosen (1973)2
Fixed
Tensor
None
Contradicted by binary pulsar data
Rastall (1976)2
Minkowski
Tensor, vector
None
Viable
VMT (1977)2
Dynamic
Scalar
2 parameters
Viable for a wide range of the parameters
MOND (1983)4
Nonmetric
Potential
Free function
Nonrelativistic theory
1 Misner, Thorne, and Wheeler (1973)
2 Will (1981)
3 Dicke (1965)
4 Milgrom (1989)
OTHER THEORIES
 below
10-8 cm s-2. In galaxies and clusters of galaxies
(with no dark matter
assumed) the gravitational fields are weaker than this, and a
breakdown of newtonian predictions having nothing to do with dark
matter is expected. With its one postulated relation, MOND ties
together a number of empirical relations in extragalactic astronomy. A
nonrelativistic gravitational theory containing the MOND relation has
been set forth, and relativistic generalizations of these ideas are
currently under study.
below
10-8 cm s-2. In galaxies and clusters of galaxies
(with no dark matter
assumed) the gravitational fields are weaker than this, and a
breakdown of newtonian predictions having nothing to do with dark
matter is expected. With its one postulated relation, MOND ties
together a number of empirical relations in extragalactic astronomy. A
nonrelativistic gravitational theory containing the MOND relation has
been set forth, and relativistic generalizations of these ideas are
currently under study.
Dicke, R. (1965). The Theoretical Significance of Experimental
Relativity. Gordon and Breach, New York.
Milgrom, M. (1989). Alternatives to dark matter.
Comments Astrophysics 13 215.
Misner, C.W., Thorne, K.S., and Wheeler, J.A. (1973).
Graviation. W.H. Freeman, San Francisco.
Will, C. (1981). Theory and Experiment in Gravitational Physics.
Cambridge University Press, Cambridge.
Will, C. (1986). Was Einstein Right? Basic Books, New York.
See also Black Holes, Stellar, Observational Evidence; Black
Holes, Theory; Dark Matter, Cosmological; Gravitational Lenses; Missing
Mass, Galactic; Pulsars, Binary; Stars, Neutron, Physical Properties and
Models.