
COSMOLOGY, POPULATION III
Bernard J. Carr
The term ``Population III'' has been used to describe two types of stars: (1) the ones which form out of the pristine gas left over after cosmological nucleosynthesis and generate the first metals; and (2) the ones which have been hypothesized to provide the dark matter in galactic halos. Stars of the first kind definitely exist, but may not warrant a special name. Those of the second kind may not exist, because galactic halos could also be composed of some sort of elementary particle, but they certainly warrant a special name if they do, and they could have many interesting cosmological consequences. Population III stars of either kind could be pregalactic, but they might also have formed during the first phase of galaxy formation.
FORMATION OF POPULATION III STARS
In the most conservative cosmological scenario, the first stars form
in the process of galaxy formation: As each protogalaxy cools and
collapses, it fragments first into a spheroidal distribution of
Population II stars, and then - if there is any gas left over - into a
rotationally supported disk of Population I stars. The problem with
this picture is that, in both of the standard scenarios for the origin
of cosmological structure, the first bound objects would be much
smaller than galaxies. For example, in the hierarchical clustering
scenario the first bound clouds have a mass of about 106
M and bind
at a redshift of order 100. Larger bound objects - like galaxies and
clusters of galaxies - would then build up through a process of
gravitational clustering. A currently popular version of this model is
the ``cold dark matter
matter'' scenario, in which the density of the universe is dominated by
some cold elementary particle like the photino or axion. In the
pancake scenario, the first objects to appear are of cluster or
supercluster scale and they form at a rather low redshift. This
applies, for example, in the ``hot dark matter'' picture, in which the
universe's mass is dominated by hot particles like neutrinos with
nonzero rest mass. However, one still expects these pancakes to
fragment into clouds of mass 108 M
and bind
at a redshift of order 100. Larger bound objects - like galaxies and
clusters of galaxies - would then build up through a process of
gravitational clustering. A currently popular version of this model is
the ``cold dark matter
matter'' scenario, in which the density of the universe is dominated by
some cold elementary particle like the photino or axion. In the
pancake scenario, the first objects to appear are of cluster or
supercluster scale and they form at a rather low redshift. This
applies, for example, in the ``hot dark matter'' picture, in which the
universe's mass is dominated by hot particles like neutrinos with
nonzero rest mass. However, one still expects these pancakes to
fragment into clouds of mass 108 M and these clouds must then
cluster
in order to form galaxies. In both scenarios, therefore, an
appreciable fraction of the universe must go into subgalactic clouds
before galaxies themselves form.
and these clouds must then
cluster
in order to form galaxies. In both scenarios, therefore, an
appreciable fraction of the universe must go into subgalactic clouds
before galaxies themselves form.
The question then arises of what happens to these clouds. In some circumstances, one expects them to be disrupted by collisions with other clouds because their cooling time is too long for them to collapse before coalescing. However, there is usually some subgalactic mass range in which the clouds survive. In this case, they could face various possible fates. They might just fragment into ordinary stars and form objects like globular clusters. On the other hand, the conditions of star formation could have been very different at early times and several alternatives have been suggested.
The first stars could have been smaller than at present because of the enhanced formation of molecular hydrogen at early epochs.
They could have been larger than at present because the lack of metals or the effects of the microwave background would increase the fragment mass.
There may have been a mixture of small and large stars; for example, angular momentum effects could lead to a disk of small stars around a central very massive star, or massive stars could form in the core of the cloud and low-mass stars in the outer regions.
The first clouds may not fragment at all, but might collapse directly to supermassive black holes or remain in purely gaseous form and become Lyman-
 clouds.
clouds.
This indicates that, although there is clearly considerable uncertainty as to the fate of the first clouds, they could well fragment into stars that are very different from the ones forming today. They certainly need to be very different if they are to produce much dark matter. Note that the appellation Population III is sometimes assigned to the first clouds rather than the first stars. However, in this case, all the stars which they spawn must also be called Population III, and this can lead to semantic confusion if the clouds fragment bimodally. It is therefore more sensible to reserve the term Population III for the stars.
It is not necessarily required that Population III stars be pregalactic. Some of the arguments for their having a different initial mass function (IMF) would also apply if they formed protogalactically, and this gives rise to a less radical hypothesis, in which the Population III objects form during the first phases of protogalactic collapse. In this case, the Population III stars or their remnants would be confined to galaxies, whereas they would be spread throughout space in the pregalactic case.
POPULATION III AS THE FIRST METAL PRODUCERS
Since heavy elements can only be generated through stellar nucleosynthesis, the existence of stars of type (1) is inevitable. However, the stars warrant a special name only if they are qualitatively different from ordinary Population II stars. For example, it would not be justified if the first metal-producing stars were merely the ones at the high-mass end of the Population II mass spectrum. For in this case they would generate the first metals simply because they evolve fastest. The introduction of a new term would only be warranted if the first metal-producing stars formed at a distinct epoch or if the IMF of the first stars was bimodal (i.e., with a distinct population of high-and low-mass stars forming in different locations).
If one studies the abundances of metal-poor stars in our own galaxy,
there is no compelling reason for supposing the first stars were
distinct from Population II. For example, field halo stars with Z
< 0.1 Z have enhancements in the ratios of O, Mg Si, and Ca to Fe by a
factor of 3 relative to the Sun, but this is naturally explained by
the fact that these elements are preferentially produced by the sort
of massive stars which would complete their evolution on the time
scale (108 yr) associated with the formation of the galactic
halo. Thus, abundance data itself does not require the existence of
Population III stars.
have enhancements in the ratios of O, Mg Si, and Ca to Fe by a
factor of 3 relative to the Sun, but this is naturally explained by
the fact that these elements are preferentially produced by the sort
of massive stars which would complete their evolution on the time
scale (108 yr) associated with the formation of the galactic
halo. Thus, abundance data itself does not require the existence of
Population III stars.
The best evidence for a distinct population of stars would be a
lower cutoff in the metallicity distribution of Population II
stars. If the first stars had the same IMF as today, with a lower
cutoff at about 0.1 M , one might expect stars smaller than 0.8
M
, one might expect stars smaller than 0.8
M (whose lifetime exceeds the age of the Universe) to display
arbitrarily low metallicity. At one time, it seemed there was a
metallicity Zmin of order 10-5 below which
no stars were found. If
this were true, it would suggest that the first stars had an IMF with
a lower cutoff above 0.8 M
(whose lifetime exceeds the age of the Universe) to display
arbitrarily low metallicity. At one time, it seemed there was a
metallicity Zmin of order 10-5 below which
no stars were found. If
this were true, it would suggest that the first stars had an IMF with
a lower cutoff above 0.8 M . For only then could they produce the
minimum enrichment Zmin without surviving until the present
epoch. This would imply that the first stars had a different IMF from
ordinary Population II stars. Unfortunately, the evidence for such a
cutoff is now in dispute: The Z distribution for Population II stars
extends well below 10-5 and there exists one object with
Z = 6 x 10-7. In any case, the number of low-Z
objects is not
necessarily incompatible with the assumption that the IMF has always
been the same; so the first stars may not have been qualitatively
different from Population II stars. Thus the introduction of the term
Population III may be unnecessary in this context.
. For only then could they produce the
minimum enrichment Zmin without surviving until the present
epoch. This would imply that the first stars had a different IMF from
ordinary Population II stars. Unfortunately, the evidence for such a
cutoff is now in dispute: The Z distribution for Population II stars
extends well below 10-5 and there exists one object with
Z = 6 x 10-7. In any case, the number of low-Z
objects is not
necessarily incompatible with the assumption that the IMF has always
been the same; so the first stars may not have been qualitatively
different from Population II stars. Thus the introduction of the term
Population III may be unnecessary in this context.
POPULATION III AS DARKMATTER PRODUCERS
The success of the standard Big Bang picture in explaining the light element abundances only applies if the baryon density is about 10% of the critical density. Since the theory of inflation requires the total density to have the critical value, this suggests that there must be much nonbaryonic dark matter (most of it unclustered). On the other hand, visible material only has about 1% of the critical density, so it seems that there must also be some baryonic dark matter. It is possible that this is in the form of a hot intergalactic medium, but there could also be enough of it to explain the dark matter in galactic halos. The dark baryons in halos cannot be in the form of ordinary gas, or else they would generate too may x-rays. They must therefore have been processed into some dark form through a first generation of pregalactic or protogalactic stars.
In principle, there are many mass ranges in which stars could
produce dark remnants. For example, stars smaller than 0.1
M would
always be dim enough to explain galactic halos and those smaller than
0.08 M
would
always be dim enough to explain galactic halos and those smaller than
0.08 M (jupiters; also called brown dwarfs) would never even ignite
their nuclear fuel. Stars in the range 0.8-4 M
(jupiters; also called brown dwarfs) would never even ignite
their nuclear fuel. Stars in the range 0.8-4 M would leave white
dwarf remnants, whereas those between 8 M
would leave white
dwarf remnants, whereas those between 8 M and some mass
MBH
(probably about 50 M
and some mass
MBH
(probably about 50 M ) would leave neutron star remnants. In either
case, the remnants would eventually cool and become dark. Stars more
massive than MBH would leave black holes. The ones
larger than 100 M
) would leave neutron star remnants. In either
case, the remnants would eventually cool and become dark. Stars more
massive than MBH would leave black holes. The ones
larger than 100 M are termed very massive objects (VMOs), and are particularly
interesting because they could collapse entirely (without any metal
ejection) due to an instability encountered in their oxygen-burning
phase. This would apply for VMOs larger than Mc
are termed very massive objects (VMOs), and are particularly
interesting because they could collapse entirely (without any metal
ejection) due to an instability encountered in their oxygen-burning
phase. This would apply for VMOs larger than Mc  200 M
200 M . Stars larger
than 105 M
. Stars larger
than 105 M are termed supermassive objects (SMOs), and would collapse
directly to black holes due to relativistic instabilities even before
nuclear burning, at least if they were metal-free. It must be stressed
that the existence of VMOs and SMOs is entirely speculative and they
are invoked primarily for the purpose of making dark matter.
are termed supermassive objects (SMOs), and would collapse
directly to black holes due to relativistic instabilities even before
nuclear burning, at least if they were metal-free. It must be stressed
that the existence of VMOs and SMOs is entirely speculative and they
are invoked primarily for the purpose of making dark matter.
Although stars can in principle produce dark remnants, various constraints require that the dark matter in galactic halos can only be baryonic if it comprises jupiters or the black hole remnants of VMOs. These constraints are summarized in Fig. 1. Low-mass stars are excluded by source count limits, other stellar remnants by nucleosynthesis and background light constraints, and supermassive black holes by dynamical considerations. At first sight, it might seem rather unlikely that Population III clouds would fragment into such objects with high efficiency, but we have seen that there are theoretical reasons for expecting the first stars to be larger or smaller than at present.
In fact, there are circumstances where dark stars form profusely even at the present epoch. Direct observational evidence that gas can be turned into low-mass stars with high efficiency may come from x-ray observations of cooling flows in the cores of rich clusters. These suggest that 90% of the gas is being turned dark, possibly as a result of the high pressure. Since such cooling flows are confined to the central galaxies in clusters, they could not explain the dark matter in galactic halos. However, one could expect analogous high-pressure flows to occur at earlier cosmological epochs, and these would have been on much smaller scales than clusters. This conclusion pertains in either the hierarchical clustering or pancake scenarios. One could envisage forming dark clusters of jupiters which then agglomerate to form galactic halos. Although VMOs are certainly rare at the present epoch, massive stars do seem to form efficiently in starburst galaxies, and they may have been more abundant in the past. VMOs would certainly have had more exciting cosmological consequences than jupiters.
Note that the formation epoch is very important for the relative distribution of baryonic and nonbaryonic dark matter. If Population III stars form before galaxies, one might expect their remnants to be distributed throughout the universe, with the ratio of the baryonic and nonbaryonic densities being the same everywhere. If they form at the same time as galaxies, one would expect the remnants to be confined to halos with the baryonic component probably dominating.
WHAT POPULATION III STARS CAN EXPLAIN
In this section we will discuss some of the cosmological consequences of Population III stars. We will mostly focus on the VMO scenario, but the last three effects could be important in a more general context. Although Population III stars can explain certain cosmological problems, it would be stressed that this does not provide unequivocal evidence for their existence, because they are not only explanation. Figure 2 summarizes the effects.
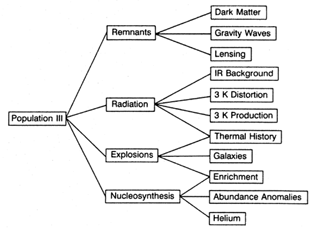
|
Figure 2. Cosmological consequences of Population III stars. |
Infrared Background
Microwave Distortions
Generation of 3-K Background
Helium Production
Dynamical Effects of Halo Holes
Gravity Waves from Black Holes
Heavy Element Prodution
Thermal History
Pregalactic Explosions
We have seen that one must distinguish between metal producing and
dark-matter-producing Population III stars. The first must exist, but
only warrant a special name if there is a lower cutoff in the
metallicity distribution of Population II stars, and it is not clear
that this is the case. The second may not exist, but, if they do, they
certainly warrant a separate name. They would have to be either
jupiters or black holes. The detection of microwave distortions would
favor the black holes option, but the claim that cooling flows make
low-mass stars may favor the jupiter option. In principle, both kinds
of Population III stars could derive from a single mass spectrum, but
that would require the IMF to be finely tuned.
 Y = 0.25(1 - Yi)2 (1 -
Yi / 2)-1, where Yi is the
initial (primordial) helium abundance. This would have profound
cosmological implications. If Yi = 0.24,
corresponding to the
conventional primordial value,
Y = 0.25(1 - Yi)2 (1 -
Yi / 2)-1, where Yi is the
initial (primordial) helium abundance. This would have profound
cosmological implications. If Yi = 0.24,
corresponding to the
conventional primordial value,  Y = 0.16, so helium would be
substantially overproduced if much of the universe went into VMOs. In
this case, the only remaining black hole candidate for the dark matter
would be SMOs in the mass range 105-106
M
Y = 0.16, so helium would be
substantially overproduced if much of the universe went into VMOs. In
this case, the only remaining black hole candidate for the dark matter
would be SMOs in the mass range 105-106
M . On the
other hand, if Yi = 0,
corresponding to no primordial production,
. On the
other hand, if Yi = 0,
corresponding to no primordial production,  Y = 0.25, which is
tantalizingly close to the standard primordial value. This raises the
question of whether the Population III VMOs invoked to produce the
dark matter might not also generate the helium which is usually
attributed to cosmological nucleosynthesis. It must be stressed,
however, that the hot Big Bang model also predicts the observed
abundances for deuterium, helium-3, and lithium. Although one can
conceive of astrophysical ways of generating these elements in a cold
universe, they are somewhat contrived.
Y = 0.25, which is
tantalizingly close to the standard primordial value. This raises the
question of whether the Population III VMOs invoked to produce the
dark matter might not also generate the helium which is usually
attributed to cosmological nucleosynthesis. It must be stressed,
however, that the hot Big Bang model also predicts the observed
abundances for deuterium, helium-3, and lithium. Although one can
conceive of astrophysical ways of generating these elements in a cold
universe, they are somewhat contrived.
 . While one
cannot definitely identify halo holes as the explanation for disk
heating (e.g., spiral density waves might also work), it is
interesting that the hole mass required can be specified so
precisely. Note that this argument does not require that the halo
object be a single hole; even a cluster of smaller holes - or indeed a
cluster of jupiters - would suffice. From a theoretical point of view,
the halo objects are more likely to be clusters because too many
supermas- sive black holes would be dragged into the galactic nucleus
by dynamical friction. Clusters would be destroyed by collisions
within the galactocentric radius where dynamical friction is
operative, providing they had a radius larger than 1 pc. Further
evidence that galactic halos comprise objects with mass of order
106 M
. While one
cannot definitely identify halo holes as the explanation for disk
heating (e.g., spiral density waves might also work), it is
interesting that the hole mass required can be specified so
precisely. Note that this argument does not require that the halo
object be a single hole; even a cluster of smaller holes - or indeed a
cluster of jupiters - would suffice. From a theoretical point of view,
the halo objects are more likely to be clusters because too many
supermas- sive black holes would be dragged into the galactic nucleus
by dynamical friction. Clusters would be destroyed by collisions
within the galactocentric radius where dynamical friction is
operative, providing they had a radius larger than 1 pc. Further
evidence that galactic halos comprise objects with mass of order
106 M may come from gravitational lensing effects. Evidence
for the jupiters themselves could come from microlensing.
may come from gravitational lensing effects. Evidence
for the jupiters themselves could come from microlensing.
 or by the Doppler tracking of interplanetary spacecraft if it is in
the range 105-1010 M
or by the Doppler tracking of interplanetary spacecraft if it is in
the range 105-1010 M . The prospects of
detecting the gravitational
radiation would be even better if the holes formed in binaries,
because one would then get both continuous waves as the binaries
spiral inward due to gravitational wave emission and a final burst of
waves when the components finally merge. This would increase the
amplitude of the waves and extend the spectrum to longer periods. One
could also hope to observe the mergers which are occurring in nearby
galaxies at the present epoch.
. The prospects of
detecting the gravitational
radiation would be even better if the holes formed in binaries,
because one would then get both continuous waves as the binaries
spiral inward due to gravitational wave emission and a final burst of
waves when the components finally merge. This would increase the
amplitude of the waves and extend the spectrum to longer periods. One
could also hope to observe the mergers which are occurring in nearby
galaxies at the present epoch.
 should produce explosive
energy with an
efficiency
should produce explosive
energy with an
efficiency  =
10-5-10-4; larger ones may explode with comparable
efficiency if they eject their envelopes during hydrogen-shell
burning. This explosive release could have an important effect on the
large-scale structure of the universe. One would expect the shock wave
generated by each exploding star (or cluster of stars) to sweep up a
shell of gas. Under suitable circumstances, this shell could
eventually fragment into more stars. If the new stars themselves
explode, one could then initiate a bootstrap process in which the
shells grow successively lager until they overlap. This mechanism has
been proposed in two contexts: (1) as a means to boost the fraction of
the universe being processed through pregalactic stars and (2) as a
way of producing the giant voids and filaments, whose existence is
indicated by observational data. An upper limit to the final shell
size in all circumstances is
=
10-5-10-4; larger ones may explode with comparable
efficiency if they eject their envelopes during hydrogen-shell
burning. This explosive release could have an important effect on the
large-scale structure of the universe. One would expect the shock wave
generated by each exploding star (or cluster of stars) to sweep up a
shell of gas. Under suitable circumstances, this shell could
eventually fragment into more stars. If the new stars themselves
explode, one could then initiate a bootstrap process in which the
shells grow successively lager until they overlap. This mechanism has
been proposed in two contexts: (1) as a means to boost the fraction of
the universe being processed through pregalactic stars and (2) as a
way of producing the giant voids and filaments, whose existence is
indicated by observational data. An upper limit to the final shell
size in all circumstances is 
 times the
current horizon size. This
is 60 Mpc for
times the
current horizon size. This
is 60 Mpc for  =
10-4 and a Hubble parameter of 100, which is just
about large enough to explain the largest voids.
=
10-4 and a Hubble parameter of 100, which is just
about large enough to explain the largest voids.
CONCLUSION
Ashman K.M. and Carr, B.J. (1988). Pregalactic cooling flows and
baryonic dark matter. Mon. Not. R. Astron. Soc. 234 219.
Beers, T.C. Preston, G.W. and Schectman, S.A. (1985). A
search for stars of very low metal abundance. Astron J. 90 2089.
Bond H.E. (1981). Where is Population III? Ap. J. 248 606.
Bond J.R. Carr, B.J., and Hogan, C.J. (1986). Spectrum and
anisotropy of the cosmic background. Ap. J. 306 428.
Carr, B.J. and Lacey, C.G. (1987). Dark clusters in galactic halos?
Ap. J. 316 23.
Carr, B.J., Bond, J.R., and Arnett, W.A. (1984). Cosmological
consequences of Population III stars. Ap. J. 277 445.
Cayrel, R. (1986). And if Population III were Population II? Astron.
Ap. 168 81.
Fabian, A.C., Nulsen, P.E.J., and Canizares, C.R. (1984).
Cooling flows in clusters of galaxies. Nature 310 733.
Hartquist, T.W. and Cameron, A.G.W. (1977). Pregalactic
nucleosynthesis. Ap. Space Sci. 48 145.
Kashlinsky, A. and Rees, M.J. (1983). Formation of Population III
stars and pregalactic evolution. Mon. Not. R. Astron. Soc.
205 955.
McDowell, J.C. (1986). The light from Population III stars. Mon.
Not. R. Astron. Soc. 223 763.
Pagel, B.E.J. (1987). Galactic chemical evolution. In The Galaxy,
G. Gilmore and B. Carswell, eds. Reidel, Dordrecht, p. 341.
Rees, M.J. (1978). Origin of pregalactic microwave background.
Nature 275 35.
Truran, J.W. (1984). Nucleosynthesis. Ann. Rev. Nucl. Part. Sci.
34 53.
White, S.D.M. and Rees, M.J. (1978). Core condensation in
heavy halos: A two-stage theory for galaxy formation and clustering.
Mon. Not. R. Astron. Soc. 183 341.
See also Background Radiation, Microwave; Cosmology, Big Bang
Theory; Cosmology, Galaxy Formation; Gravitational Radiation.
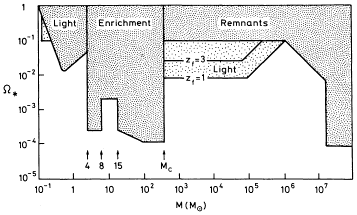
 * is the density in units of the critical
cosmological value;
* is the density in units of the critical
cosmological value;