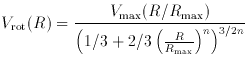Annu. Rev. Astron. Astrophys. 1979. 17: 135-87 Copyright © 1979 by Annual Reviews. All rights reserved

3.1 Observed Rotation Curves

Roberts (1975a) has dramatically illustrated the difficulty of using the older optical rotation curves to probe the outer mass distributions of spiral galaxies. A convenient measure of the optical extent of a galaxy is the Holmberg radius (Holmberg 1958), which is the major-axis radius at a surface brightness of 26.5 photographic mag arcsec^-2. Roberts found that the median extent of optical rotation curves published up to 1975 was only 0.3 Holmberg radii. These curves typically showed a steep rise in rotational velocity near the nucleus, then a short section of leveling off [e.g. NGC 157 (Burbidge et al. 1961)]. There the data ended, usually because the surface brightness of the galaxy was so low that further measurements were impossible.

Until recently it was customary to assume that in such cases the turnover of the rotation curve had been reached and that the rotational velocity declined smoothly past the turnover radius, eventually to reach the Keplerian falloff, V R^-1/2, at large R. Considerable theoretical machinery was constructed to model the curve and deduce the mass distribution and total mass from the measured points. Burbidge & Burbidge (1975) give a comprehensive description of these techniques; Bosma (1978) provides a useful additional discussion of Toomre (1963) disk models. A simple and commonly used approximation is based on Brandt's (1960) parametrization of the rotation curve:

(1)

where V_max is the maximum rotational velocity, R_max is the radius at which the maximum rotational velocity occurs, and n is a shape parameter which determines how rapidly the curve reaches a Keplerian falloff. The value of n is determined by fitting the curve up to the last measured point. If it is assumed that the velocity beyond this radius is adequately approximated by the Brandt model, the total mass of the galaxy, M_T, is (3/2)^3/n V²_max R_max / G.

Table 1. Galaxies with extended rotation curves

In the context of extragalactic astronomy a decade ago, the Brandt model and its relatives were a logical way to model the outer regions of a galaxy. After all, the light was falling off rapidly at the last measured point, and in several galaxies the rotation curve also seemed to be falling appreciably as well [e.g. NGC 5055 (Burbidge et al. 1960)]. However, workers at that time were well aware that a convenient extrapolation was being used which might not represent reality. ``One does not know how much the tail wags the dog,'' cautioned Burbidge and Burbidge.

Radio 21-cm observations, which in many galaxies now extend well past the Holmberg radius, do not confirm this extrapolation. The radio rotation curves remain flat to the limit of observation, in some cases beyond 50 kpc, indicating much larger total masses than given by the Brandt formula. This result was strongly hinted at in early observations by Shostak & Rogstad (1973), Rogstad et al. (1973, 1974), and Seielstad & Wright (1973). Further evidence came from observations of M31 by Roberts (Roberts 1975a, Roberts & Whitehurst 1975) and from an early compilation of rotation curves by Huchtmeier (1975). These initial results have been overwhelmingly confirmed by the more recent work of Bosma (1978), Krumm, and Salpeter (Salpeter 1978), and other references summarized in Table 1. At the same time, Rubin, Ford and co-workers (summarized by Rubin et al. 1978) have pushed optical observations to greater radii by exploiting improvements in spectrograph and image-tube design. 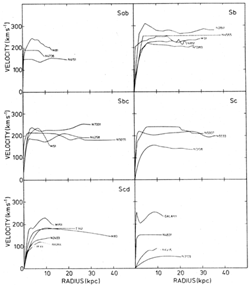A montage of representative modern rotation curves collected by Bosma is shown in Figure 2.

Figure 2. Rotation curves of 25 galaxies of various morphological types from Bosma (1978).

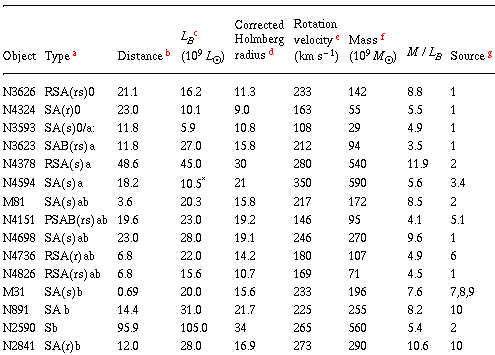
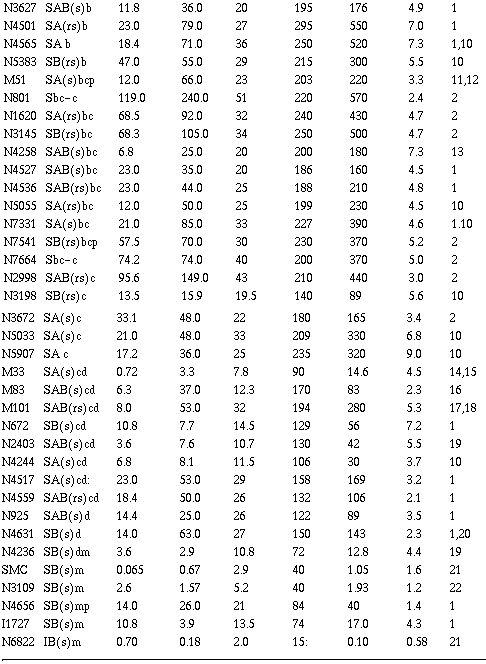
There are now approximately 50 galaxies for which reliable rotation curves exist out to large radii (see Table 1). Very few are seen to turn over at all, and only three (M81, M51, and M101) show significant declines. All three of these galaxies, however, have nearby companions which may well perturb the outer H I. Furthermore, M81 has a large bulge which might produce a turnover in velocity because of its strong central condensation, while the H I in M101 shows strongly asymmetric motions on opposite sides of the major axis. In short, all three of these galaxies might well be atypical objects.

The reality of flat rotation curves has been questioned on several grounds. Doubts have been raised, for example, as to whether the H I is truly in circular motion. There are indeed good reasons to fear that within the inner regions of galaxies, ionized gas is not always in circular orbit. For example, marked asymmetries in the inner rotation curves amounting to ~ 100 km sec^-1 exist in both M31 (Rubin & Ford 1971, de Harveng & Pellet 1975) and M81 (Goad 1976). Moreover, the emission-line rotation curves of bulge-dominated early-type spirals do not rise nearly as steeply as the light distributions suggest they should. The brightness profiles of such bulges near the nuclei are similar to those of elliptical galaxies (Kormendy 1977a, Burstein 1978, Kormendy & Bruzual 1978), and by analogy we would expect the rotation curve to rise to a sharp maximum within a few arc seconds, provided the mass-to-light ratio is uniform. In the three Sa galaxies with observed rotation curves, NGC 4378 (Rubin et al. 1978 NGC 4594 (Schweizer 1978), and NGC 681 (Burbidge, Burbidge & Prendergast 1965), this steep rise is not observed. NGC 4594 is an especially puzzling case; M / L_B in the nucleus based on the velocity dispersion is 12.6 (Williams 1977) yet is only 0.26 at 1 kpc according to the rotation curve (Schweizer 1978). Since the spectrum and colors (S. Faber, unpublished) give no hint of a significant change in the mass-to-light ratio of the stellar population, we seriously doubt that the ionized gas is in circular motion. Einasto (1972) has expressed a similar opinion that observed velocities in the ionized gas in the bulge of M31 are too low to reflect true rotation. Lack of adequate spatial resolution and noncircular motions due to bar-like distortions (Bosma 1978) are additional complications affecting rotation curves near nuclei.

For these reasons, rotation curves in the inner regions of galaxies might not be useful indicators of the mass distribution. We prefer to concentrate here on the outer regions, where noncircular motions and lack of angular resolution pose fewer problems. Even at large radii, however, the interpretation of these observations is a subtle matter. For example, sidelobes on radio telescopes could produce a fictitious flat rotation curve due to spillover from the bright HI at smaller radii. The initial results of Krumm and Salpeter (Salpeter 1978) were criticized for this reason by Sancisi (1978), but F. Briggs, N. Krumm, and E. Salpeter (in preparation) have since carefully calibrated the sidelobes of the Arecibo dish, and the final data should be free from this effect. Moreover, it is hard to see how sidelobes could affect the entire body of available data, since 21-cm measurements have been with many different instruments, single dishes as well as interferometers. The fact that flat rotation curves are also measured with optical techniques further strengthens this conclusion.

For all these reasons, it seems most unlikely that flat rotation curves are merely an artifact of observational errors. Even so, various dynamical arguments have been advanced which question the conventional identification with local circular velocity. For example, the outermost H I layer in many spirals is significantly warped out of the main plane of the galaxy (e.g. Rogstad, Lockhart & Wright 1974, Sancisi 1976). These warps might be accompanied by motions which mimic a flat rotation curve along the major axis if the inclination of the warp were properly arranged. However, for several of the galaxies in Table 1, warps have been fully modelled using the entire information available in two dimensions, and a flat rotation curve still persists. Further, the sheer bulk of the data is beginning to tell: it is hard to see how warps with random projection factors could conspire to produce a flat rotation curve in so many different galaxies.

It has also been suggested that H I at large radii might represent recent infall and not yet be in dynamical equilibrium. However, with few exceptions (e.g. M101) the velocities on opposite sides of the galaxy are reasonably symmetric, and circular motions (with a possible warp) satisfactorily fit the observations leaving relatively small residuals (Bosma 1978). Furthermore, because the flat portions in many galaxies extend over a large fraction of the observable radius, one would be forced to conclude that a large portion of the gas is out of equilibrium.

In summary, we feel that no generally valid alternative explanation has been put forward for these flat rotation curves and that the observations and their implications must therefore be taken very seriously.

For an assumed spherical mass distribution and V_rot constant with radius, the mass within radius R increases linearly with radius and the surface mass density declines as R_-1. Since the surface brightness of spirals declines exponentially (Freeman 1970, Schweizer 1976), this simple model predicts a strong increase in the local mass-to-light ratio projected on the sky as long as the rotation curve stays flat. Bosma (1978) finds that the precise form of this increase depends rather sensitively on the nature of the mass model assumed, whether spherical or disk. However, the increase in local M / L cannot be made to disappear completely by varying the model. Bosma (1978) and Roberts & Whitehurst (1975) have obtained local values of M / L_B of 100-300 in seven spirals at the outer limits of the observations, much larger than M / L_B for the stellar population in the solar neighborhood (Section 2.1).

Despite the complications mentioned above, mass determination using rotation curves is a relatively simple procedure. There are none of the statistical projection factors and group membership decisions which plague the analysis of binary and group motions. Based on present data and standard interpretations, it seems relatively certain that dark material is being detected.

The amount of extra mass actually implied by these rotation curves is itself relatively trivial; galaxy masses on average have perhaps doubled over the older optical estimates, not enough to satisfy the mass discrepancy for groups and clusters, as we shall see. Nevertheless, flat rotation curves have profound implications for the problem of missing mass, first because the detection of unseen matter is relatively secure and second because at least some of the missing mass seems to be associated with individual galaxies themselves.