Copyright © 1979 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1979. 17:
135-87 Copyright © 1979 by Annual Reviews. All rights reserved |
3.2 Mass-to-Light Ratios
The discovery of flat rotation curves has thrown out any hopes we might have had of estimating the total masses of galaxies based on an extrapolation of their rotation curves. Such an extrapolation would necessarily involve an assumption as to how far the flat rotation curves continue, which is something one certainly would not want to guess at this time. The notion of total masses based on internal motions still appears frequently in today's literature and is one we would like to discourage; the derivation invariably involves assumptions which are unjustified, and the results can be misleading.
If we confine ourselves to what is actually measured, we are led
inevitably to the concept of mass and mass-to-light ratio within a
specified radius. Ideally one would like to use a radius related to
some natural length-scale for the galaxy, for example the e-folding
length for exponential disks (
-1). This is not realizable at present
because -1 is known
for too few galaxies. As a practical necessity, we
adopt an isophotal radius, even though this radius is systematically
smaller for systems of low surface brightness, such as late-type
spirals and irregulars. The Holmberg radius RHO seems
a good choice
because it is comparable in size to the extent of presently available
rotation curves and is easily derived by transformation from the large
body of diameter data in the Second Reference Catalogue.
Table 1 collects information on galaxies available at present with published rotation curves which extend to at least 0.5 Holmberg radii and for which inclination corrections can be reliably estimated. The great majority have velocity curves extending nearly to RHO or beyond. For estimating the mass within RHO, elaborate techniques which exploit every bump and wiggle in the rotation curve seem to us unnecessary. For reasons discussed earlier, the inner sections of the measured curves may not contain useful information and furthermore do not strongly influence the total mass determination. Moreover, if one is looking for trends in mass and M / L with Hubble type, simplicity is a virtue. Insofar as possible, one must avoid the use of assumptions which vary with type since such procedures may themselves introduce spurious trends.
For all these reasons, it seems justified simply to assume that the mass is spherically distributed within RHO and to calculate the mass at RHO as MHO = RHO V2HO / G, where VHO is the observed velocity of rotation at the Holmberg radius. The assumption of a spherical distribution of material has some theoretical justification (see Section 8) but is basically unproven at this time. The use of highly flattened spheroids would yield masses roughly 35% smaller.
|
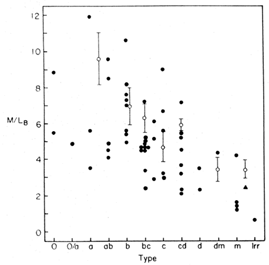
Figure 3. Blue mass-to-light ratios within the Holmberg radius versus morphological type. Black dots: individual galaxies in Table 1. Open circles: logarithmic means from single-dish measurements by Dickel & Rood (1978). Triangle: late-type DDO irregulars from Fisher & Tully (1975). |
The resultant values of M / LB are computed on the system of luminosities described in Section 1 and are plotted in Figure 3 versus morphological type. A trend is apparent in that later types seem to have lower M / LB than early types. This conclusion is weak, however, because the number of late-type spirals in the sample is small.
We have therefore used single dish 21-cm profiles to verify this trend. Single-dish observations are useful here because the steep-sided H I profile yields a velocity width that is closely related to the velocity of rotation in the galaxy. Many workers have converted such velocity widths into total masses using the Brandt approximation (Roberts 1969, S. Peterson 1978, Balkowski 1973, Dickel & Rood 1978). We have assumed instead a flat rotation curve and calculated the mass within the Holmberg radius, as described above.
Our results are based on the extensive observations of Dickel and Rood for 121 disk galaxies. Comparison of 21-cm line widths with rotational velocities at RHO for 16 galaxies in common with Table 1 indicates that <V2> of Dickel and Rood is 25% larger than <V2rot> from Table 1. We applied this correction to the single-dish masses. The results for M / LB (logarithmic means) based on this sample are shown as open circles in Figure 3, where the error bars reflect only the formal error in the mean, not the possible systematic errors. These data confirm the trend with type suggested by the individual rotation curves.
To further strengthen the data on the latest types, we used the indicative masses of Fisher & Tully (1975) for DDO irregular galaxies, adjusted to our system. The result is plotted as a triangle in Figure 3, and agrees with the low M / LB for late types found from the other two methods. Recent data by Shostak (1978) (not plotted) also support the correlation in Figure 3 (see also Nordsieck 1973).
In summary, a trend in M / LB within the Holmberg radius seems fairly well established. Whether or not a trend exists in total mass-to-light ratio cannot be determined from rotational velocities at the present time.
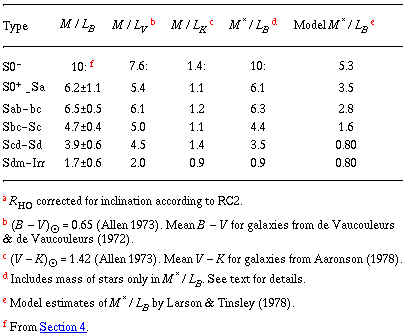
An estimate for S0's from Section 4 is also included. For completeness, M / LV and M / LK are also given, transformed from M / LB using the data described in the notes. Interestingly, the trend in M / L with morphological type seen with B luminosities disappears when K magnitudes are used, and M / LK is approximately constant. This is strong confirmation of the prediction of this effect made on quite different quasi-theoretical grounds by Aaronson et al. (1979).
The observed trend in M / LB with type is generally what one would expect from variations in stellar content along the Hubble sequence. For example, Larson & Tinsley (1978) have found that M / LB is well correlated with B - V for model stellar populations over a wide range of ages. In their work, the mass refers to stars alone. To compare with their results, we must correct the observed M / LB for mass due to gas. To do this, we have made the crude assumption that Robert's (1975b) global values of MHI / LB versus Hubble type apply also within the Holmberg radius and have neglected any contribution by molecular hydrogen.
The result is the column labeled M* / LB in Table 2, to be compared with Larson and Tinsley's model M* / LB, also in Table 2. Exact agreement is not expected, since the amount of material in evolved degenerate stars in the model is quite uncertain. Furthermore any matter in dark envelopes is not included in the Larson-Tinsley model. Nevertheless, within a scaling factor, the models appear to represent the total range of M* / LB rather well. The detailed agreement is not quite so good, however; the strong change in color of spirals from type Sa to Sd would suggest a noticeable decrease in M* / LB whereas the data show only a slight decrease.
Finally, we note that M / LB for spirals within the Holmberg radius is ~ 4-6, not much greater than the local M / LB for the solar neighborhood, which is ~ 1-3 (Section 2). This comparison indicates that unseen matter does not strongly dominate the mass within RHO. This result is consistent with the Ostriker-Caldwell model of the Milky Way; their model contains only 25% dark matter within 20 kpc (roughly the Holmberg radius for our galaxy).
|