3. DETERMINATION OF

As illustrated in Figure 2a, the cosmological constant has had a long and volatile history in cosmology. There have been many reasons to be skeptical about a non-zero value of the cosmological constant. To begin with, there is a discrepancy of 120 orders of magnitude between current observational limits and estimates of the vacuum energy density based on current standard particle theory ( e.g. Carroll, Press and Turner 1992). A further difficulty with a non-zero value for is that it appears coincidental that we are now living at a special epoch when the cosmological constant has begun to affect the dynamics of the Universe (other than during a time of inflation). It is also difficult to ignore the fact that historically a non-zero has been called upon to explain a number of other apparent crises, and moreover, adding additional free parameters to a problem always makes it easier to fit data.

However, despite the strong arguments have been made for = 0, there are growing reasons for a renewed interest in a non-zero value. Although the current value of is small compared to the observed limits, there is no known physical principle that demands = 0 (e.g., Carroll, Press & Turner 1992). Although Einstein originally introduced an arbitrary constant term, standard particle theory and inflation now provide a physical interpretation of : it is the energy density of the vacuum (e.g., Weinberg 1989). Finally, a number of observational results can be explained with a low _m and _m + = 1: for instance, the observed large scale distribution of galaxies, clusters, and voids described previously, in addition to the recent results from type Ia supernovae described below. In addition, the discrepancy between the ages of the oldest stars and the expansion age (exacerbated if _m = 1) can be resolved.

Excitement has recently been generated by the results from two groups studying type Ia supernovae at high redshift (one team's results were reported at this meeting by Ariel Goobar). Both groups have found that the high redshift supernovae are fainter (and therefore further), on average, than implied by either an open (_m = 0.2) or a flat, matter-dominated (_m = 1) universe. The observed differences are ~ 0.25 and 0.15 mag, (Reiss et al. 1998 and Perlmutter et al. 1998a, respectively), or equivalently ~ 13% and 8% in distance. A number of tests have been applied to search for possible systematic errors that might produce this observed effect, but none has been identified. Taken at face value, these results imply that the vacuum energy density of the Universe, (), is non-zero.

The early results from these two groups have evolved as more data have become available. Perlmutter et al. (1997) first reported results based on a sample of 7 high-redshift (z ~ 0.4) supernovae. Initially, they found evidence for a high matter density _m ~ 0.9 ± 0.3, with a value of consistent with zero. However, with the subsequent discovery of a z ~ 0.8 supernova, Perlmutter et al. (1998a) found instead that a low-mass density (_m ~ 0.2) universe was preferred. The second, independent group obtained preliminary results based on 4 supernovae which were also consistent with a lower matter density (Garnavich et al. 1998). The sample sizes have now grown larger, with 10 supernovae being reported by Reiss et al. (1998) and 42 supernovae being reported by Perlmutter et al. (1999). These two new larger data sets are yielding consistent conclusions, and the supernovae are now indicating a non-zero and positive value for ~ 0.7, and a small matter density, _m ~ 0.3, under the assumption that _m + = 1. If a flat universe is not assumed, the best fit to the Perlmutter et al. data yields _m = 0.73, = 1.32. The Hubble diagram for both the nearby (Hamuy et al. 1996) and the distant (Reiss et al. 1998) samples of supernovae are shown in Figure 3.

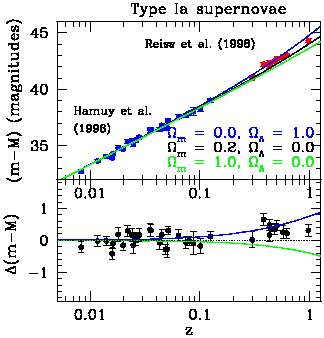
Figure 3 (top panel): The Hubble diagram for type Ia supernovae from Hamuy et al. (1996) and Reiss et al. (1998). Plotted is the distance modulus in magnitudes versus the logarithm of the redshift. Curves for various cosmological models are indicated. (bottom panel): Following Reiss et al. (1998), the difference in magnitude between the observed data points compared to an open (m = 0.2) model is shown. The distant supernovae are fainter by 0.25 magnitudes, on average, than the nearby supernovae.

The advantages of using type Ia supernovae for measurements of are many. The dispersion in the nearby type Ia supernova Hubble diagram is very small (0.12 mag or 6% in distance, as reported by Reiss et al. 1996). They are bright and therefore can be observed to large distances. In principle, at z ~ 1, the shape of the Hubble diagram alone can be used to separate _m and , independent of the nearby, local calibration sample (Goobar & Perlmutter 1995). Potential effects due to evolution, chemical composition dependence, changing dust properties are all amenable to empirical tests and calibration.

A possible weakness of all of the current supernova studies is that the luminosities of the high-redshift supernovae are all measured relative to the same set of local supernovae. Although in the future, estimates of at high redshift will be possible using the shape of the Hubble diagram alone (Goobar & Perlmutter 1995), at present, the evidence for comes from a differential comparison of the nearby sample of supernovae at z < 1, with those at z ~ 0.3-0.8. Hence, the absolute calibrations, completeness levels, and any other systematic effects pertaining to both datasets are critical. For several reasons, the search techniques and calibrations of the nearby and the distant samples are different. Moreover, the intense efforts to search for high-redshift objects have now led to the situation where the nearby sample is now smaller than the distant samples. While the different search strategies may not necessarily introduce systematic differences, increasing the nearby sample will provide an important check. Such searches are now underway by several groups.

Although a 0.25 mag difference between the nearby and distant samples appears large, the history of measurements of H₀ provides an interesting context for comparison. In the case of H₀ determinations, a difference of 0.25 mag in zero point only corresponds to a difference between 60 and 67 km/sec/Mpc! Current differences in the published values for H₀ result from a number of arcane factors: the adoption of different calibrator galaxies, the adoption of different techniques for measuring distances, treatment of reddening and metallicity, and differences in adopted photometric zero point. In fact, despite the considerable progress on the extragalactic distance scale and the Hubble constant, recent H₀ values tend to range from about 60 to 80 km/sec/Mpc (see next section). (As recently as five years ago, there was a factor of 2 discrepancy in these values, corresponding to a difference of 1.5 mag.)

In interpreting the observed difference between nearby and distant supernovae, it is also important to keep in mind that, for the known properties of dust in the interstellar medium, the ratio of total-to-selective absorption, (R_B = A_B / E(B - V)), (the value by which the colors are multiplied to correct the blue magnitudes), is ~ 4. Hence, very accurate photometry and colors are required to ultimately understand this issue. A relative error of only 0.03 mag in color could contribute 0.12 mag to the observed difference in magnitude.

Further tests and limits on may come from gravitational lens number density statistics (Fukugita et al. 1990; Fukugita and Turner 1991; Kochanek 1996), plus more stringent limits to the numbers of close-separation lenses. The numbers of strong gravitational lenses detected depends on the volume surveyed; hence, the probability that a quasar will be lensed is a very sensitive function of . In a flat universe with = 0, almost an order of magnitude fewer lenses are predicted than for a universe with = 1.

If the current results from supernovae are correct, then the numbers of close-separation lenses should be significantly larger than predicted for = 0 models. Complications for the lens number density statistics arise due to a number of factors which are hard to quantify in an error estimate, and which become increasingly more important for smaller values of : for example, galaxies evolve (and perhaps merge) with time, galaxies contain dust, the properties of the lensing galaxies are not well-known (in particular, the dark matter velocity dispersion is unknown), and the numbers of lensing systems for which this type of analysis has been carried out is still very small. However, the sample of known lens systems is steadily growing, and new limits from this method will be forthcoming.

The gravitational lens number density limits from Kochanek (1996) are < 0.66 (95% confidence) for _m + = 1. However, more recently, Cheng & Krauss (1998) have reinvestigated the sensitivity of this method to various factors. As Kochanek and Cheng & Krauss have underscored, the uncertainties in modelling of the lensing galaxies (generally as isothermal spheres with core radii), the observed luminosity functions, core radii of the galaxies, and the resulting magnification bias (that results due to the fact that the lensed quasar images are amplified, and hence, easier to detect than if there were no lensing) all need to be treated carefully. Also, as Cheng & Krauss emphasize, the optical depth for lensing depends on the velocity dispersion to the fourth power and hence, better accuracies in the velocity dispersions are required. Cheng & Krauss conclude that systematic uncertainties currently dominate the results from this method, but that a flat universe with a low value of _m cannot be excluded.