


One of the striking features of the CBR fluctuations is that they appear to be noncausal. The CBR fluctuations were largely imprinted at the time of last-scattering, about 300,000 years after the bang. However, there are fluctuations on length scales much larger than 3000,000 light years! How could a causal process imprint fluctuations on scales larger than the light-travel distance since the time of the bang? The answer is inflation, but to see how that works, let's define the problem more exactly.
First consider the evolution of the Hubble radius with the scale factor a (t): (1)
In a k = 0 matter-dominated universe the age is related to
H by t = (2/3)H-1, so
RH = (3/2)t. In the early radiation-dominated
universe t = (1/2)H-1, so RH
= 2t.
On length scales smaller than RH it is possible to
move material
around and make an imprint upon the universe. Scales larger than
RH are ``beyond the Hubble radius,'' and the expansion of the
universe prevents the establishment of any perturbation on scales
larger than RH.
Next consider the evolution of some physical length scale
Now let us form the dimensionless ratio L
Since RH = a / dota, and
In the standard scenario,
For illustration, let us take
Sometime during the early evolution of the universe the expansion was
such that dotdota > 0, which as we have just seen, requires an
unusual equation of state with
Including the inflationary phase, our best guess for the different
epochs in the history of the universe is given in
Table 1. There is basically nothing known about
the stringy
phase, if indeed there was one. The earliest phase we have
information about is the inflationary phase. As we shall see, the
information we have is from the quantum fluctuations during inflation,
which were imprinted upon the metric, and can be observed as CBR
fluctuations and the departures from homogeneity and isotropy in the
matter distribution, e.g., the power spectrum. A lot of effort has
gone into studying the end of inflation. It was likely that there was
a brief period of matter domination before the universe became
radiation dominated. Very little is known about this period after
inflation. Noteworthy events that might have occurred during this
phase include baryogenesis, phase transitions, and generation of dark
matter. We do know that the universe was radiation dominated for
almost all of the first 10,000 years. The best evidence of the
radiation-dominated era is primordial nucleosynthesis, which is a
relic of the radiation-dominated universe in the period 1 second to 3
minutes. The earliest picture of the matter-dominated era is the CBR.
Here, I am interested in events during the inflationary era. The
first issue is how to imagine a universe dominated by vacuum energy
making a transition to a matter-dominated or radiation-dominated
universe. A simple way to picture this is by the action of a scalar
field
If the inflaton is completely decoupled, then it will oscillate about
the minimum of the potential, with the cycle-average of the energy
density decreasing as a-3, i.e., a matter-dominated universe.
But at the end of inflation the universe is cold and frozen in a
low-entropy state: the only degree of freedom is the zero-momentum
mode of the inflaton field. It is necessary to ``defrost'' the
universe and turn it into a ``hot'' high-entropy universe with many
degrees of freedom in the radiation. Exactly how this is accomplished
is still unclear. It probably requires the inflaton field to be
coupled to other degrees of freedom, and as it oscillates, its energy
is converted to radiation either through incoherent decay, or through
a coherent process involving very complicated dynamics of coupled
oscillators with time-varying masses. In either case, it is necessary
to extract the energy from the inflaton and convert it into radiation.
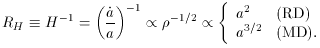
 .
Clearly, any physical length scale changes in expansion in proportion
to a (t).
.
Clearly, any physical length scale changes in expansion in proportion
to a (t).

 / RH. If L
is smaller than unity, the length scale is smaller than the Hubble radius and
it is possible to imagine some microphysical process establishing
perturbations on that scale, while if L is larger than unity, no
microphysical process can account for perturbations on that scale.
/ RH. If L
is smaller than unity, the length scale is smaller than the Hubble radius and
it is possible to imagine some microphysical process establishing
perturbations on that scale, while if L is larger than unity, no
microphysical process can account for perturbations on that scale.

 a, the
ratio L is
proportional to dota, and dotL scales as dotdota, which
in turn is proportional to -(
a, the
ratio L is
proportional to dota, and dotL scales as dotdota, which
in turn is proportional to -( + 3p). There are two possible
scenarios for dotL depending upon the sign of
+ 3p). There are two possible
scenarios for dotL depending upon the sign of  + 3p:
+ 3p:
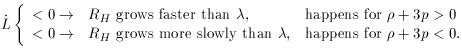
 + 3p > 0, RH grows faster than
+ 3p > 0, RH grows faster than
 . This is illustrated by
the left-hand side of
Fig. 5.
. This is illustrated by
the left-hand side of
Fig. 5.
 to be the present length
to be the present length
 8 =
8h-1 Mpc,
the scale beyond which perturbations today are
in the linear regime. The physical length scale, which today is
8 =
8h-1 Mpc,
the scale beyond which perturbations today are
in the linear regime. The physical length scale, which today is
 8, was smaller in
the early universe by a factor of
a (t) / a0, where a0 is the scale
factor today. Today, the Hubble
radius is H0-1 ~ 3000 h-1
Mpc. Of course, today
8, was smaller in
the early universe by a factor of
a (t) / a0, where a0 is the scale
factor today. Today, the Hubble
radius is H0-1 ~ 3000 h-1
Mpc. Of course, today  8
is well within the current Hubble radius. But in the standard picture,
RH grows faster than
8
is well within the current Hubble radius. But in the standard picture,
RH grows faster than  , and there must
therefore have been a time when
the comoving length scale that corresponds to
, and there must
therefore have been a time when
the comoving length scale that corresponds to  8 was larger
than RH
8 was larger
than RH
 + 3p < 0. This is referred to as
``accelerated expansion'' or ``inflation.''
+ 3p < 0. This is referred to as
``accelerated expansion'' or ``inflation.''
Table 1. Different epochs in the history of the
universe and the associated tempos of the expansion rate.

 with potential V
(
with potential V
( ). Let's imagine the scalar field
is displaced from the minimum of its potential as illustrated in
Fig. 6. If the energy density of the universe is
dominated
by the potential energy of the scalar field
). Let's imagine the scalar field
is displaced from the minimum of its potential as illustrated in
Fig. 6. If the energy density of the universe is
dominated
by the potential energy of the scalar field  , known as the
inflaton, then
, known as the
inflaton, then  + 3p will be negative. The vacuum energy
disappears when the scalar field evolves to its minimum.
+ 3p will be negative. The vacuum energy
disappears when the scalar field evolves to its minimum.
(1) Here and throughout the paper ``RD''
is short for radiation dominated, and ``MD'' implies matter
dominated. Back