


3.1 Quantum Fluctuations
During inflation there are quantum fluctuations in the inflaton field. Since the total energy density of the universe is dominated by the inflaton potential energy density, fluctuations in the inflaton field lead to fluctuations in the energy density. Because of the rapid expansion of the universe during inflation, these fluctuations in the energy density are frozen into super-Hubble-radius-size perturbations. Later, in the radiation or matter-dominated era they will come within the Hubble radius as if they were noncausal perturbations.
The spectrum and amplitude of perturbations depend upon the nature of
the inflaton potential. Mukhanov
[3]
has developed a very nice
formalism for the calculation of density perturbations. One starts
with the action for gravity (the Einstein-Hilbert action) plus a
minimally-coupled scalar inflaton field  :
:
Here R is the Ricci curvature scalar. Quantum fluctuations result
in perturbations in the metric tensor
where g
i.e., the action in conformal time
The simple matter of calculating the perturbation spectrum for a
noninteracting scalar field in Minkowski space will give the amplitude
and spectrum of the density perturbations. The problem is that the
solution to the field equations depends upon the background field
evolution through the dependence of the mass of the field upon z.
Different choices for the inflaton potential V(
Before proceeding, now is a useful time to remark that in addition to
scalar density perturbations, there are also fluctuations in the
transverse, traceless component of the spatial part of the metric.
These fluctuations (known as tensor fluctuations) can be thought of as
a background of gravitons.
Although the scalar and tensor spectra depend upon V(
In addition to the primordial spectrum characterized by n and r,
in order to compare to data it is necessary to specify cosmological
parameters (H0, the present expansion rate;
The specification of the dark matter is by how ``hot'' the dark
matter was when the universe first became matter dominated. If the
dark matter was really slow at that time, then it is referred to as
cold dark matter. If the dark matter was reasonably hot when the
universe became matter dominated, then it is called hot dark matter.
Finally, the intermediate case is called warm dark matter. Neutrinos
with a mass in the range 1 eV to a few dozen eV would be hot dark
matter. Light gravitinos, as appear in gauge-mediated supersymmetry
breaking schemes, is an example of warm dark matter. By far the most
popular dark matter candidate is cold dark matter. Examples of cold
dark matter are neutralinos and axions.
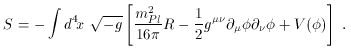
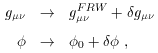

 0 (t) is the
classical solution for the homogeneous,
isotropic evolution of the inflaton. The action describing the
dynamics of the small perturbations can be written as
0 (t) is the
classical solution for the homogeneous,
isotropic evolution of the inflaton. The action describing the
dynamics of the small perturbations can be written as
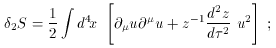
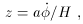
 (d
(d 2 =
a2 (t) dt2) for
a scalar field in Minkowski space, with mass-squared
mu2 = -z-1
d2 z / d
2 =
a2 (t) dt2) for
a scalar field in Minkowski space, with mass-squared
mu2 = -z-1
d2 z / d 2. Here, the scalar field u is a
combination of metric fluctuations
2. Here, the scalar field u is a
combination of metric fluctuations  gµ
gµ and scalar
field fluctuations
and scalar
field fluctuations 
 . This scalar field is related to the
amplitude of the density perturbation.
. This scalar field is related to the
amplitude of the density perturbation.
 ) results in
different background field evolutions, and hence, different spectra
and amplitudes for the density perturbations.
) results in
different background field evolutions, and hence, different spectra
and amplitudes for the density perturbations.
 ), for most
potentials they can be characterized by QRMSPS
(the amplitude
of the scalar and tensor spectra on large length scales added in
quadrature), n (the scalar spectral index describing the best
power-law fit of the primordial scalar spectrum), r (the ratio of
the tensor-to-scalar contribution to C2 in the angular power
spectrum), and nT ( the tensor spectral index
describing the best
power-law fit of the primordial tensor spectrum). For single-field,
slow-roll inflation models, there is a relationship between
nT and
r, so in fact there are only three independent variables.
Furthermore, the amplitude of the fluctuations often depends upon a
free parameter in the potential, and the spectra are normalized by
QRMSPS. This leads to a characterization of a
wide-range of
inflaton potentials in terms of two numbers, n and r.
), for most
potentials they can be characterized by QRMSPS
(the amplitude
of the scalar and tensor spectra on large length scales added in
quadrature), n (the scalar spectral index describing the best
power-law fit of the primordial scalar spectrum), r (the ratio of
the tensor-to-scalar contribution to C2 in the angular power
spectrum), and nT ( the tensor spectral index
describing the best
power-law fit of the primordial tensor spectrum). For single-field,
slow-roll inflation models, there is a relationship between
nT and
r, so in fact there are only three independent variables.
Furthermore, the amplitude of the fluctuations often depends upon a
free parameter in the potential, and the spectra are normalized by
QRMSPS. This leads to a characterization of a
wide-range of
inflaton potentials in terms of two numbers, n and r.
 0, the ratio
of the present mass-energy density to the critical density - a
spatially flat universe has
0, the ratio
of the present mass-energy density to the critical density - a
spatially flat universe has  0 = 1;
0 = 1;  B, the ratio of the
present baryon density to the critical density;
B, the ratio of the
present baryon density to the critical density;  DM the
ratio of the present dark-matter density to the critical density; and
DM the
ratio of the present dark-matter density to the critical density; and
 , the value of the
cosmological constant), as well as the nature of the dark matter.
, the value of the
cosmological constant), as well as the nature of the dark matter.