


In this school, the matter of neutrino masses has been reviewed in
great detail. A neutrino of mass m contributes to
contributes to 
 h2 an amount
h2 an amount
If the mass of the neutrino is significantly less than 0.1 eV, then
its contribution to
More promising than neutrino hot dark matter is cold dark matter. The
most promising candidate for cold dark matter is the lightest
supersymmetric particle, presumably a neutralino. Neutralino dark
matter has been well studied and reviewed
[4].
The next most popular dark-matter candidate is the axion. Although the
axion is very light, since its origin is from a condensate, it is very
cold. Axion dark matter has also been well studied and well reviewed
[5].
There are presently several experiments searching for cosmic
neutralinos and cosmic axions. Both types of searches seem
sensitive enough to discover the relic dark matter, although it will
take quite some time (and probably another generation of experiments)
to completely cover the parameter space.
Neutralinos are an example of a thermal relic. A thermal relic is
assumed to be in local thermodynamic equilibrium (LTE) at early times.
The equilibrium abundance of a particle, say relative to the
entropy density, depends upon the ratio of the mass of the particle to
the temperature. If we define the variables Y
A particle will track its equilibrium abundance so long as reactions
which keep the particle in chemical equilibrium can proceed rapidly
enough. Here, rapidly enough means on a timescale more rapid than the
expansion rate of the universe H. When the reactions becomes
slower than the expansion rate, then the particle can no longer track
its equilibrium value and thereafter Y is constant. When this
occurs, the particle is said to be ``frozen out.'' A schematic
illustration of this is given in Fig. 8.
The more strongly interacting the particle, the longer it stays in
LTE, and the smaller its freeze-out abundance. Thus, the more weakly
interacting the particle, the larger its present abundance. The
freeze-out value of Y is related to the mass of the particle and its
annihilation cross section (here characterized by
Since the contribution to
The mass of WIMPS usually considered for dark matter run from a
microvolt for axions to several dozen GeV for neutralinos. With the
exception of massive magnetic monopoles, the possibility
of dark matter particles of GUT-scale mass is not usually considered,
because thermal relics of this mass would be expected to be
over abundant by several orders of magnitude.
Recently, the idea that dark matter may be supermassive has
received a lot of attention. Since wimpy little dark matter particles
with mass less than a TeV are called WIMPS, dark matter particles of
really hefty mass of 1012 to 1016 GeV seem to be
more than WIMPS, so they are referred to as WIMPZILLAS.
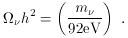
 0 is dynamically unimportant.
0 is dynamically unimportant.
 nX / s and
x = MX / T, where nX is the
number density of WIMP (weakly interacting
massive particle) X with mass
MX and s ~ T3 is the entropy
density,
Y
nX / s and
x = MX / T, where nX is the
number density of WIMP (weakly interacting
massive particle) X with mass
MX and s ~ T3 is the entropy
density,
Y  exp(-x) for
x >> 1, while Y ~ constant for x << 1.
exp(-x) for
x >> 1, while Y ~ constant for x << 1.
 0) by
0) by
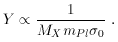
 is
proportional to MX nX, which
in turn is proportional to MXY, the present
contribution to
is
proportional to MX nX, which
in turn is proportional to MXY, the present
contribution to  from a thermal relic is (to first approximation) independent of
the mass, and only depends on the mass
indirectly through the dependence of the annihilation cross section on
mass. The largest that the annihilation cross section can be is roughly
MX-2. This implies that large-mass WIMPS
would have such a
small annihilation cross section that their present abundance would be
too large. Thus, one expects a maximum mass for a thermal WIMP, which
turns out to be a few hundred TeV.
from a thermal relic is (to first approximation) independent of
the mass, and only depends on the mass
indirectly through the dependence of the annihilation cross section on
mass. The largest that the annihilation cross section can be is roughly
MX-2. This implies that large-mass WIMPS
would have such a
small annihilation cross section that their present abundance would be
too large. Thus, one expects a maximum mass for a thermal WIMP, which
turns out to be a few hundred TeV.