


5.2 WIMPZILLAS - Size Does Matter
The simple assumption that the dark matter (DM) is a thermal relic is
surprisingly
restrictive. The limit  X
X  1 implies that the mass of a
DM relic must be less than about 500 TeV
[6]. The standard
lore is that the hunt for DM should concentrate on particles with mass
of the order of the weak scale and with interactions with ordinary
matter on the scale of the weak force. This has been the driving force
behind the vast effort in DM detectors.
1 implies that the mass of a
DM relic must be less than about 500 TeV
[6]. The standard
lore is that the hunt for DM should concentrate on particles with mass
of the order of the weak scale and with interactions with ordinary
matter on the scale of the weak force. This has been the driving force
behind the vast effort in DM detectors.
But recent developments in understanding how matter is created in the early universe suggests the possibility that DM might be naturally composed of nonthermal supermassive states. The supermassive dark matter (WIMPZILLA) X may have a mass many orders of magnitude larger than the weak scale, possibly as large as the Grand Unified Theory (GUT) scale. It is very intriguing that these considerations resurrect the possibility that the dark matter might be charged or even strongly interacting!
The second condition for WIMPZILLAS is that the particle must not have been
in equilibrium when it froze out (i.e., it is not a thermal
relic), otherwise  X would be larger than one.
A sufficient condition for nonequilibrium is that the
annihilation rate (per particle) must be smaller than the expansion
rate: n
X would be larger than one.
A sufficient condition for nonequilibrium is that the
annihilation rate (per particle) must be smaller than the expansion
rate: n  |v| <
H, where n is the number density,
|v| <
H, where n is the number density,  |v| is
the annihilation rate times the Møller flux factor, and H is the
expansion rate. Conversely, if the WIMPZILLA was created at some
temperature T* and
|v| is
the annihilation rate times the Møller flux factor, and H is the
expansion rate. Conversely, if the WIMPZILLA was created at some
temperature T* and  X < 1, then it is easy to show that
it could not have attained equilibrium. To see this, assume Xs
were created in a radiation-dominated universe at temperature
T*.
Then
X < 1, then it is easy to show that
it could not have attained equilibrium. To see this, assume Xs
were created in a radiation-dominated universe at temperature
T*.
Then  X is
given by
X is
given by  X =
X =

 (T*/T0) MX nX(T*)
/
(T*/T0) MX nX(T*)
/ 
 (T*),
where T0 is the present temperature (ignoring dimensionless
factors of order unity.) Using the fact that
(T*),
where T0 is the present temperature (ignoring dimensionless
factors of order unity.) Using the fact that 
 (T*) =
H(T*) MPl
T*2, we find
nX(T*) /
H(T*)
= (
(T*) =
H(T*) MPl
T*2, we find
nX(T*) /
H(T*)
= ( X /
X / 
 ) T0 MPl
T* / MX. We may safely take the
limit
) T0 MPl
T* / MX. We may safely take the
limit  |v| <
MX-2, so
nX(T*)
|v| <
MX-2, so
nX(T*) |v| /
H(T*) must
be less than (
|v| /
H(T*) must
be less than ( X /
X / 
 )
T0 MPl T* /
MX3.
Thus, the requirement for nonequilibrium is
)
T0 MPl T* /
MX3.
Thus, the requirement for nonequilibrium is
This implies that if a nonrelativistic particle with
MX
An attractive origin for WIMPZILLAS is during the defrosting phase after
inflation. It is important to realize that it is not necessary to
convert a significant fraction of the available energy into massive
particles; in fact, it must be an infinitesimal amount. If a fraction
In one extreme we might assume that the vacuum energy of inflation is
immediately converted to radiation, resulting in a reheat temperature
TRH. In this case
A second (and more plausible) scenario is that reheating is not
instantaneous, but is the result of the decay of the inflaton
field. In this approach the radiation is produced as the inflaton
decays. The WIMPZILLA density is
found by solving the coupled system of equations for the inflaton
field energy, the radiation density, and the WIMPZILLA mass density. The
calculation has been recently reported in Ref.
[8], with
result
The large difference in WIMPZILLA masses in the two reheating scenarios
arises because the peak temperature is much larger in the second
scenario, even with identical TRH. Because the temperature
decreases as a-3/8 (a is the scale factor)
during most of the
reheating period in the second scenario, it must have once been much
greater than TRH. The evolution of the temperature
is given in Fig. 9.
If we assume the radiation spectrum did not depart
grossly from thermal, the effective temperature having once been
larger than TRH implies that the density of particles
with enough
energy to create WIMPZILLAS was larger. Denoting as T2
the maximum
effective temperature for the second scenario, we find
T2 / TRH
~ (M
Another way to produce WIMPZILLAS after inflation is in a preliminary stage
of reheating called ``preheating''
[9], where nonlinear
quantum effects may lead to an extremely effective dissipational
dynamics and explosive particle production. Particles can be created
in a broad parametric resonance with a fraction of the energy stored
in the form of coherent inflaton oscillations at the end of inflation
released after only a dozen oscillation periods. A crucial
observation for our discussion is that particles with mass up to
1015 GeV may be created during preheating
[10,
11,
12],
and that their distribution is nonthermal. If these particles are stable,
they may be good candidates for WIMPZILLAS.
To study how the creation of WIMPZILLAS takes place in preheating, let us
take the simplest chaotic inflation potential:
V (
For a reheating temperature of the order of 100 GeV, the present
abundance of WIMPZILLAS with mass MX ~
1014 GeV is given by
Another possibility which has been recently investigated is the
production of very massive particles by gravitational mechanisms
[15,
16].
In particular, the desired abundance of WIMPZILLAS may be
generated during the transition from the inflationary phase to a
matter/radiation dominated phase as the result of the expansion of the
background spacetime acting on vacuum quantum fluctuations of the dark
matter field
[15].
A crucial side-effect of the inflationary
scenarios is the generation of density perturbations. A related
effect, which does not seem to have attracted much attention, is the
possibility of producing matter fields due to the rapid change in the
evolution of the scale factor around the end of inflation. Contrary to
the first effect, the second one contributes to the homogeneous
background energy density that drives the cosmic expansion, and is
essentially the familiar ``particle production'' effect of
relativistic field theory in external fields.
Very massive particles may be created in a nonthermal state with
sufficient abundance to achieve critical density today by the
classical gravitational effect on the vacuum state at the end of
inflation. Mechanically, the particle creation scenario is similar to
the inflationary generation of gravitational perturbations that seed
the formation of large-scale structures. However, the quantum
generation of energy density fluctuations from inflation is associated
with the inflaton field, which dominated the mass density of the
universe, and not a generic sub-dominant scalar field.
If 0.04
The observation of anisotropy in the cosmic background radiation
does not fix He uniquely, but using
TRH
The distinguishing feature of this mechanism
[15] is
the capability of generating particles with mass of the order of the
inflaton mass even when the WIMPZILLA interacts only extremely weakly (or
not at all!) with other particles, including the inflaton. This
feature makes the gravitational production mechanism quite model
independent and, therefore, more appealing to us than the one
occurring at preheating.
WIMPZILLAS can also be produced in theories where
inflation is completed by a first-order phase transition
[17]. In
these scenarios, the universe decays from its false vacuum state by
bubble nucleation
[18].
When bubbles form, the energy of the
false vacuum is entirely transformed into potential energy in the
bubble walls, but as the bubbles expand, more and more of their energy
becomes kinetic and the walls become highly relativistic. Eventually
the bubble walls collide.
During collisions, the walls oscillate through each other
[19]
and the kinetic energy is dispersed into low-energy scalar waves
[19,
20].
If these soft scalar quanta carry quantum numbers
associated with some spontaneously broken symmetry, they may even lead
to the phenomenon of nonthermal symmetry restoration
[21]. We
are, however, more interested in the fate of the potential energy of
the walls, MP = 4
Suppose now that the WIMPZILLA is some fermionic degree of freedom X and
that it couples to the inflaton field by the Yukawa coupling g
In conclusion, a large fraction of the DM in the
universe may be made of WIMPZILLAS of mass
greatly exceed the electroweak scale - perhaps as large as the GUT
scale. This is made possible by the fact that the WIMPZILLAS were created in a
nonthermal state and never reached chemical equilibrium with the
primordial plasma.
ACKNOWLEDGEMENTS
This work was supported in part by the Department of Energy, as well
as NASA under grant
number NAG5-7092. The hospitality of Tom Ferbel
and the inquisitiveness of the students were greatly appreciated.
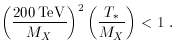
 200
TeV was created at T* < MX with a
density low enough to result in
200
TeV was created at T* < MX with a
density low enough to result in
 X
X  1, then its abundance must
have been so small that
it never attained equilibrium. Therefore, if there is some way to
create WIMPZILLAS in the correct abundance to give
1, then its abundance must
have been so small that
it never attained equilibrium. Therefore, if there is some way to
create WIMPZILLAS in the correct abundance to give  X ~ 1,
nonequilibrium is guaranteed.
X ~ 1,
nonequilibrium is guaranteed.
 of the available energy
density is in the form of a
massive, stable X particle, then
of the available energy
density is in the form of a
massive, stable X particle, then  X =
X = 

 (TRH / T0), where TRH is
the ``reheat'' temperature. For
(TRH / T0), where TRH is
the ``reheat'' temperature. For
 X = 1, this
leads to the limit
X = 1, this
leads to the limit 
 10-17 (109 GeV /
TRH).
10-17 (109 GeV /
TRH).
 X can be calculated by integrating
the Boltzmann equation with initial condition NX = 0
at T = TRH.
One expects the X density to be suppressed by
exp(-2MX / TRH);
indeed, one finds
X can be calculated by integrating
the Boltzmann equation with initial condition NX = 0
at T = TRH.
One expects the X density to be suppressed by
exp(-2MX / TRH);
indeed, one finds  X ~ 1 for MX /
TRH ~ 25 +
0.5 ln(MX2 <
X ~ 1 for MX /
TRH ~ 25 +
0.5 ln(MX2 <  |v| >), in agreement with previous
estimates [7] that
for TRH ~ 109 GeV, the
WIMPZILLA mass would be about 2.5 x 1010 GeV.
|v| >), in agreement with previous
estimates [7] that
for TRH ~ 109 GeV, the
WIMPZILLA mass would be about 2.5 x 1010 GeV.
 X ~
MX2 <
X ~
MX2 <  |v| >
(2000 TRH / MX)7. For a reheat
temperature as
low as 109 GeV, a particle of mass 1013 GeV can be
produced in
sufficient abundance to give
|v| >
(2000 TRH / MX)7. For a reheat
temperature as
low as 109 GeV, a particle of mass 1013 GeV can be
produced in
sufficient abundance to give  X ~ 1.
X ~ 1.
 /
/ 
 )1/4 >> 1, where
)1/4 >> 1, where 
 is the
effective decay rate of the inflaton. See
[8] for details.
is the
effective decay rate of the inflaton. See
[8] for details.
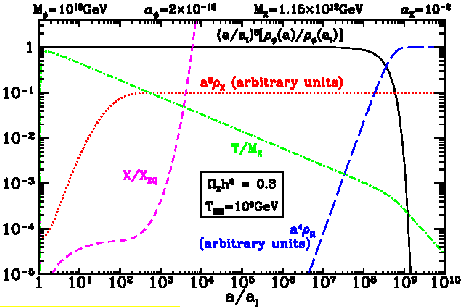
Figure 9. The evolution of energy densities and
T/MX as a function
of the scale factor. Also shown is X/XEQ.
 ) =
M
) =
M 2
2  2 / 2 with
M
2 / 2 with
M ~
1013 GeV. We assume
that the interaction term between the WIMPZILLA and the inflaton field is of
the type g2
~
1013 GeV. We assume
that the interaction term between the WIMPZILLA and the inflaton field is of
the type g2 2
|X|2. Quantum fluctuations of the X field with
momentum
2
|X|2. Quantum fluctuations of the X field with
momentum 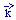 during
preheating approximately obey the
Mathieu equation, X''k + [A (k) - 2q
cos2z] Xk = 0, where q =
g2
during
preheating approximately obey the
Mathieu equation, X''k + [A (k) - 2q
cos2z] Xk = 0, where q =
g2
 2 / 4
M
2 / 4
M 2, A (k) =
(k2 + MX2) /
M
2, A (k) =
(k2 + MX2) /
M 2 + 2q (primes
denotes differentiation with respect to z = M
2 + 2q (primes
denotes differentiation with respect to z = M t). Particle
production occurs above the line A = 2q in an instability
strip of
width scaling as q1/2 for large q. The
condition for broad
resonance, A - 2q
t). Particle
production occurs above the line A = 2q in an instability
strip of
width scaling as q1/2 for large q. The
condition for broad
resonance, A - 2q  q1/2
[10],
becomes (k2 +
M2X) / M
q1/2
[10],
becomes (k2 +
M2X) / M 2
2  g bar
g bar / M
/ M , which yields
EX2 =
k2 + MX2
, which yields
EX2 =
k2 + MX2  g bar
g bar M
M for the typical energy of
particles produced in preheating. Here bar
for the typical energy of
particles produced in preheating. Here bar is the amplitude of
the oscillating inflaton field
[9].
The resulting
estimate for the typical energy of particles at the end of the broad
resonance regime for M
is the amplitude of
the oscillating inflaton field
[9].
The resulting
estimate for the typical energy of particles at the end of the broad
resonance regime for M ~ 10-6 MPl is
EX ~
10-1 g1/2 sqrt (M
~ 10-6 MPl is
EX ~
10-1 g1/2 sqrt (M MPl) ~ g1/2 1015 GeV.
Supermassive X bosons can be produced by the broad parametric
resonance for EX > MX, which leads
to the estimate that X
production will be possible if MX <
g1/2 1015
GeV. For g2
~ 1 one would have copious production of X particles as heavy as
1015 GeV, i.e., 100 times greater than the inflaton mass,
which may be many orders of magnitude greater than the reheat
temperature. Scatterings of X fluctuations off the zero mode of the
inflaton field considerably limits the maximum magnitude of X
fluctuations to be < X2 >max
MPl) ~ g1/2 1015 GeV.
Supermassive X bosons can be produced by the broad parametric
resonance for EX > MX, which leads
to the estimate that X
production will be possible if MX <
g1/2 1015
GeV. For g2
~ 1 one would have copious production of X particles as heavy as
1015 GeV, i.e., 100 times greater than the inflaton mass,
which may be many orders of magnitude greater than the reheat
temperature. Scatterings of X fluctuations off the zero mode of the
inflaton field considerably limits the maximum magnitude of X
fluctuations to be < X2 >max  M
M 2 /
g2
[13].
For example, < X2 >max
2 /
g2
[13].
For example, < X2 >max  10-10 MPl2 in the case
MX = 10 M
10-10 MPl2 in the case
MX = 10 M . This restricts
the corresponding number density of created X-particles.
. This restricts
the corresponding number density of created X-particles.
 X ~ 1 if
X ~ 1 if
 ~ 10-10. This
small fraction
corresponds to < X2 > ~ 10-12
MPl2 at the
end of the preheating stage, a value naturally achieved for WIMPZILLA mass
in the GUT range
[13].
The creation of WIMPZILLAS through preheating
and, therefore, the prediction of the present value of
~ 10-10. This
small fraction
corresponds to < X2 > ~ 10-12
MPl2 at the
end of the preheating stage, a value naturally achieved for WIMPZILLA mass
in the GUT range
[13].
The creation of WIMPZILLAS through preheating
and, therefore, the prediction of the present value of  X, is
very model dependent. The inflaton might preferably decay through
parametric resonance into very light boson fields so that the end of
the preheating stage and of the corresponding value of
< X2 > depends upon the coupling of the inflaton field
not only
to the WIMPZILLA, but also to other degrees of freedom. It is
encouraging, however, that it is possible to produce supermassive
particles during preheating that are as massive as 1012
TRH.
Details of WIMPZILLA production in preheating can be found in
[14].
X, is
very model dependent. The inflaton might preferably decay through
parametric resonance into very light boson fields so that the end of
the preheating stage and of the corresponding value of
< X2 > depends upon the coupling of the inflaton field
not only
to the WIMPZILLA, but also to other degrees of freedom. It is
encouraging, however, that it is possible to produce supermassive
particles during preheating that are as massive as 1012
TRH.
Details of WIMPZILLA production in preheating can be found in
[14].
 MX / He
MX / He  2
[15],
where He is the
Hubble constant at the end of inflation, DM produced gravitationally
can have a density today of the order of the critical density. This
result is quite robust with respect to the fine details of the
transition between the inflationary phase and the matter-dominated
phase. The only requirement is that
2
[15],
where He is the
Hubble constant at the end of inflation, DM produced gravitationally
can have a density today of the order of the critical density. This
result is quite robust with respect to the fine details of the
transition between the inflationary phase and the matter-dominated
phase. The only requirement is that
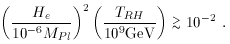
 sqrt (MPl He),
we find that the mechanism is effective only when He
sqrt (MPl He),
we find that the mechanism is effective only when He  109 GeV
(or, MX
109 GeV
(or, MX  108 GeV).
108 GeV).

 R2, where
R2, where
 is the energy per unit
area of the bubble with radius R. The bubble walls can be imagined
as a coherent state of inflaton particles, so that the typical energy
E of the products of their decays is simply the inverse thickness of
the wall, E ~
is the energy per unit
area of the bubble with radius R. The bubble walls can be imagined
as a coherent state of inflaton particles, so that the typical energy
E of the products of their decays is simply the inverse thickness of
the wall, E ~  -1. If the bubble walls are highly
relativistic when they collide, there is the possibility of quantum
production of nonthermal particles with mass well above the mass
of the inflaton field, up to energy
-1. If the bubble walls are highly
relativistic when they collide, there is the possibility of quantum
production of nonthermal particles with mass well above the mass
of the inflaton field, up to energy  -1 =
-1 =  M
M ,
,
 being the
relativistic Lorentz factor.
being the
relativistic Lorentz factor.
 barX X. One
can treat
barX X. One
can treat  (the
bubbles or walls) as a
classical, external field and the WIMPZILLA as a quantum field in the
presence of this source. This amounts to ignoring the backreaction of
particle production on the evolution of the walls, but this is
certainly a good approximation in our case. The number of WIMPZILLA
particles created in the collisions from the wall's potential energy
is NX ~ fX MP /
MX, where fX parametrizes the fraction of the
primary decay products that are WIMPZILLAS. The
fraction fX will depend in general on the masses and
the couplings
of a particular theory in question. For the Yukawa coupling g, it
is fX
(the
bubbles or walls) as a
classical, external field and the WIMPZILLA as a quantum field in the
presence of this source. This amounts to ignoring the backreaction of
particle production on the evolution of the walls, but this is
certainly a good approximation in our case. The number of WIMPZILLA
particles created in the collisions from the wall's potential energy
is NX ~ fX MP /
MX, where fX parametrizes the fraction of the
primary decay products that are WIMPZILLAS. The
fraction fX will depend in general on the masses and
the couplings
of a particular theory in question. For the Yukawa coupling g, it
is fX  g2 ln(
g2 ln( M
M / 2
MX)
[20,
22].
Supermassive particles in bubble collisions are
produced out of equilibrium and they never attain chemical
equilibrium. Assuming TRH
/ 2
MX)
[20,
22].
Supermassive particles in bubble collisions are
produced out of equilibrium and they never attain chemical
equilibrium. Assuming TRH  100 GeV, the present abundance of
WIMPZILLAS is
100 GeV, the present abundance of
WIMPZILLAS is  X ~ 1 if g ~ 10-5
X ~ 1 if g ~ 10-5
 1/2. Here
1/2. Here
 -1 << 1 denotes the
fraction of the bubble energy at
nucleation which has remained in the form of potential energy at the
time of collision. This simple analysis indicates that the correct
magnitude for the abundance of X particles may be naturally obtained
in the process of reheating in theories where inflation is terminated
by bubble nucleation.
-1 << 1 denotes the
fraction of the bubble energy at
nucleation which has remained in the form of potential energy at the
time of collision. This simple analysis indicates that the correct
magnitude for the abundance of X particles may be naturally obtained
in the process of reheating in theories where inflation is terminated
by bubble nucleation.