Polarization in the microwave background is generated through the polarization-dependent cross-section for Thomson scattering. Consider Thomson scattering of an incoming unpolarized beam of electromagnetic radiation by an electron; this discussion closely follows those in Kosowsky (1996) and Kosowsky (1998). The total scattering cross-section, defined as the radiated intensity per unit solid angle divided by the incoming intensity per unit area, is given by
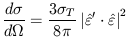
| (9) |
where 
T is the total
Thomson cross section and
the vectors 
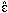and
'
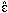are unit vectors in the planes perpendicular to the propogation directions
which are aligned with the outgoing and incoming polarization,
respectively. Consider first a nearly monochromatic, unpolarized
incident plane wave of intensity I' and cross-sectional area
B
which is scattered into the z-axis direction.
Defining the y-axes of the incoming and outgoing coordinate
systems to be in the scattering plane, the Stokes parameters
of the outgoing beam, defined with respect to the x-axis,
follow from Eq. (9) as
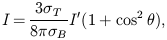
| (10) |
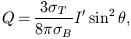
| (11) |
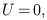
| (12) |
where 
is the angle between the
incoming and outgoing beams.
By symmetry, Thomson scattering can generate no circular polarization,
so V = 0 always and will not be considered further.
(Note that Eqs. (3) give the well-known result that
sunlight from the horizon at midday is linearly polarized parallel
to the horizon).
The net polarization produced by the scattering of an incoming,
unpolarized ratiation field of intensity
I'(,
) is determined
by integrating Eqs. (3) over all incoming directions. Note
that the coordinate system for each incoming direction
must be rotated about the z-axis so that the outgoing Stokes parameters
are all defined with respect to a common coordinate system, using the
transformation of Q and U under rotations. The result is
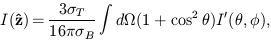
| (13) |
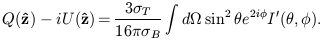
| (14) |
Expanding the incident radiation field in spherical harmonics,
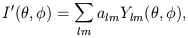
| (15) |
leads to the following expressions for the outgoing Stokes parameters:
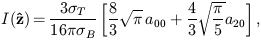
| (16) |
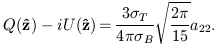
| (17) |
Thus polarization is generated along the outgoing z-axis provided that
the a22 quadrupole moment of the incoming radiation is
non-zero. To
determine the outgoing polarization in a direction making an angle
with the z-axis, the same physical incoming field
must be multipole expandedin a coordinate system rotated through the
Euler angle ;
the rotated multipole coefficients are
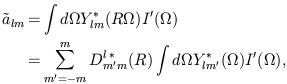
| (18) |
where R is the rotation operator and
Dlm'm is the Wigner
D-symbol. (For a wonderfully complete reference on representations
of the rotation group, see
Varshalovich et al. (1988)).
In the rotated coordinate system,
the multipole coefficient generating polarization is
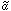22 by
Eqs. (3). The unrotated multipole components which contribute
to polarization will all have l = 2 by the orthogonality of the
spherical harmonics. If the incoming radiation field is independent of
, as it will be for individual
Fourier components of a density perturbation, then
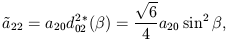
| (19) |
which has used an explicit expression for the reduced D-symbol dlm'm. The outgoing Stokes parameters are finally
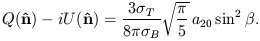
| (20) |
In other words, an azimuthally-symmetric
radiation field will generate a polarized scattered field if
it has a non-zero a20 multipole component, and the magnitude
of the scattered polarization will be proportional to
sin2.
Since the incoming field is real, a20 will be real,
U = 0,
and the polarization orientation will be in the plane of the z-axis
and the scattering direction. Similar relationships can be derived
for radiation fields which are not azimuthally symmetric, which
occur in the cases of vector and tensor metric perturbations.
In short, what this section shows is that unpolarized quadrupolar radiation fields get Thomson scattered into polarized radiation fields. This is the key fact which must be appreciated to understand why the microwave background should be polarized and what the magnitude of the polarization is expected to be.