Polarized light is conventionally described in terms of the
Stokes parameters, which are presented in any optics text.
Consider a
nearly monochromatic plane electromagnetic wave propogating in
the z-direction; nearly monochromatic here means that its frequency
components are closely distributed around its mean frequency
0.
The components of the wave's electric field vector at a given
point in space can be written as
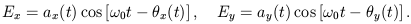
| (1) |
The requirement that the wave is nearly monochromatic guarantees
that the amplitudes ax and ay and
the phase angles
x and
y will vary slowly
relative to the inverse frequency of the wave. If some
correlation exists between the two components in
Eq. (1), then the wave is polarized.
The Stokes parameters are defined as the following time averages:
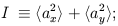
| (2) |
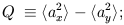
| (3) |
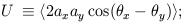
| (4) |
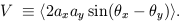
| (5) |
The averages are over times long compared to the inverse frequency of the wave. The parameter I gives the intensity of the radiation which is always positive and is equivalent to the temperature for blackbody radiation. The other three parameters define the polarization state of the wave and can have either sign. Unpolarized radiation, or ``natural light,'' is described by Q = U = V = 0.
The parameters I and V are physical observables independent
of the coordinate system, but Q and U depend on the
orientation of the x and y axes. If a given wave is
described by the parameters Q and U for a certain
orientation of the coordinate system, then after a rotation of
the x - y plane through an angle
, it is
straightforward to verify that the same wave is now
described by the parameters
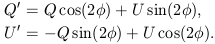
| (6) |
From this transformation it is easy to see that the quantity Q2 + U2 is invariant under rotation of the axes, and the angle
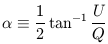
| (7) |
transforms to 
-
under a rotation by
and thus
defines a constant orientation, which physically is parallel
to the electric field of the wave.
The Stokes parameters are a useful description of
polarization because they are additive for incoherent
superposition of radiation; note this is not true for the
magnitude or orientation of polarization.
While polarization has a magnitude and an orientation, it
is not a vector quantity because the orientation does not
have a direction, describing only the plane in which the
electric field of the wave oscillates. Mathematically,
the Stokes parameters are identical for an axis rotation
through an angle of 
, whereas for a
vector, such a
rotation would lead to an inverted vector and a full rotation
through 2 is required to return to
the same situation. The transformation law in Eq. (6) is characteristic
of the second-rank tensor
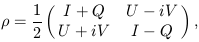
| (8) |
which also corresponds to the quantum mechanical density matrix for an ensemble of photons (Kosowsky, 1996) (the matrix is 2 by 2 because the photon has two helicity states).