


Before decoupling, the matter in the universe has significant pressure because it is tightly coupled to radiation. This pressure counteracts any tendency for matter to collapse gravitationally. Formally, the Jeans mass is greater than the mass within a horizon volume for times earlier than decoupling. During this epoch, density perturbations will set up standing acoustic waves in the plasma. Under certain conditions, these waves leave a distinctive imprint on the power spectrum of the microwave background, which in turn provides the basis for precision constraints on cosmological parameters. This section reviews the basics of the acoustic oscillations.
In their classic 1996 paper, Hu and Sugiyama transformed the basic equations describing the evolution of perturbations into an oscillator equation. Combining the zeroth moment of the photon Boltzmann equation with the baryon Euler equation for a given k-mode in the tight-coupling approximation (mean baryon velocity equals mean radiation velocity) gives

| (27) |
where 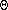 0 is the
zeroth moment of the temperature distribution
function (proportional to the photon density perturbation),
R = 3
0 is the
zeroth moment of the temperature distribution
function (proportional to the photon density perturbation),
R = 3 b
/ 4
b
/ 4
 is proportional to the scale factor a,
H =
is proportional to the scale factor a,
H = 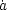 / a is the
conformal Hubble parameter, and the sound speed is
given by cs2 = 1 / (3 + 3R). (All overdots
are derivatives with respect to conformal time.)
/ a is the
conformal Hubble parameter, and the sound speed is
given by cs2 = 1 / (3 + 3R). (All overdots
are derivatives with respect to conformal time.)
 and
and
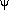 are the scalar metric
perturbations in the Newtonian gauge; if we neglect the anisotropic
stress, which is generally small in conventional cosmological
scenarios, then
are the scalar metric
perturbations in the Newtonian gauge; if we neglect the anisotropic
stress, which is generally small in conventional cosmological
scenarios, then 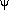 = -
= -
 . But the details are not very
important. The equation represents damped, driven oscillations of
the radiation density, and the various physical effects are
easily identified. The second term on the left side is the damping
of oscillations due to the expansion of the universe. The third
term on the left side is the restoring force due to the pressure,
since cs2 = dP /
d
. But the details are not very
important. The equation represents damped, driven oscillations of
the radiation density, and the various physical effects are
easily identified. The second term on the left side is the damping
of oscillations due to the expansion of the universe. The third
term on the left side is the restoring force due to the pressure,
since cs2 = dP /
d . On the
right side, the first two terms
depend on the time variation of the gravitational potentials, so these
two are the source of the Integrated Sachs-Wolfe effect. The final
term on the right side is the driving term due to the gravitational
potential perturbations. As Hu and Sugiyama emphasized, these damped,
driven acoustic oscillations account for all of the structure in the
microwave background power spectrum.
. On the
right side, the first two terms
depend on the time variation of the gravitational potentials, so these
two are the source of the Integrated Sachs-Wolfe effect. The final
term on the right side is the driving term due to the gravitational
potential perturbations. As Hu and Sugiyama emphasized, these damped,
driven acoustic oscillations account for all of the structure in the
microwave background power spectrum.
A WKB approximation to the homogeneous equation with no driving source terms gives the two oscillation modes (Hu and Sugiyama 1996)

| (28) |
where the sound horizon rs is given by

| (29) |
Note that at times well before matter-radiation equality, the sound speed is
essentially constant,
cs = 1 / 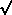 3, and
the sound horizon is
simply proportional to the causal horizon.
In general, any perturbation with wavenumber k will set up an
oscillatory behavior in the primordial plasma described by a linear
combination of the two modes in Eq. (28). The relative
contribution of the modes will be determined by the initial conditions
describing the perturbation.
3, and
the sound horizon is
simply proportional to the causal horizon.
In general, any perturbation with wavenumber k will set up an
oscillatory behavior in the primordial plasma described by a linear
combination of the two modes in Eq. (28). The relative
contribution of the modes will be determined by the initial conditions
describing the perturbation.
Equation (27) appears to be simpler than it actually
is, because  and
and
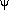 are the total gravitational potentials
due to all matter and radiation, including the photons which the
left side is describing. In other words, the right side of the
equation contains an implicit dependence on
are the total gravitational potentials
due to all matter and radiation, including the photons which the
left side is describing. In other words, the right side of the
equation contains an implicit dependence on
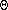 0. At the expense
of pedagogical transparency, this situation can be remedied by
considering separately the potential from the photon-baryon fluid and
the potential from the truly external sources, the dark matter and
neutrinos. This split has been performed by
Hu and White (1996).
The resulting equation, while still an oscillator equation, is much more
complicated, but must be used for a careful physical analysis of
acoustic oscillations.
0. At the expense
of pedagogical transparency, this situation can be remedied by
considering separately the potential from the photon-baryon fluid and
the potential from the truly external sources, the dark matter and
neutrinos. This split has been performed by
Hu and White (1996).
The resulting equation, while still an oscillator equation, is much more
complicated, but must be used for a careful physical analysis of
acoustic oscillations.
The initial conditions for radiation perturbations for a given
wavenumber k can be broken into two categories, according to whether
the gravitational potential perturbation from the baryon-photon fluid,
 b
b , is nonzero or zero as
, is nonzero or zero as
 -> 0. The
former case is known as ``adiabatic'' (which is somewhat of a misnomer
since adiabatic technically refers to a property of a time-dependent process)
and implies that nb /
n
-> 0. The
former case is known as ``adiabatic'' (which is somewhat of a misnomer
since adiabatic technically refers to a property of a time-dependent process)
and implies that nb /
n , the ratio of baryon to photon number
densities, is a constant in space. This case must couple to the cosine
oscillation mode since it requires
, the ratio of baryon to photon number
densities, is a constant in space. This case must couple to the cosine
oscillation mode since it requires
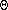 0
0
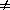 0 as
0 as
 -> 0. The simplest
(i.e. single-field) models of
inflation produce perturbations with adiabatic initial conditions.
-> 0. The simplest
(i.e. single-field) models of
inflation produce perturbations with adiabatic initial conditions.
The other case is termed ``isocurvature'' since the fluid
gravitational potential perturbation
 b
b , and hence the
perturbations to the spatial curvature, are zero.
In order to arrange such a perturbation,
the baryon and photon densities must vary in such a way that they
compensate each other: nb /
n
, and hence the
perturbations to the spatial curvature, are zero.
In order to arrange such a perturbation,
the baryon and photon densities must vary in such a way that they
compensate each other: nb /
n varies, and thus these
perturbations are in entropy, not curvature. At an early enough time,
the temperature perturbation in a given k mode must arise entirely
from the Sachs-Wolfe effect, and thus isocurvature perturbations
couple to the sine oscillation mode. These perturbations arise from
causal processes like phase transitions: a phase transition cannot
change the energy density of the universe from point to point, but it
can alter the relative entropy between various types of matter
depending on the values of the fields involved.
The potentially most interesting cause of isocurvature perturbations
is multiple dynamical fields in inflation. The fields will exchange
energy during inflation, and the field values will vary stochastically
between different points in space at the end of the phase transition,
generically giving isocurvature along with adiabatic perturbations
(Polarski and
Starobinsky 1994).
varies, and thus these
perturbations are in entropy, not curvature. At an early enough time,
the temperature perturbation in a given k mode must arise entirely
from the Sachs-Wolfe effect, and thus isocurvature perturbations
couple to the sine oscillation mode. These perturbations arise from
causal processes like phase transitions: a phase transition cannot
change the energy density of the universe from point to point, but it
can alter the relative entropy between various types of matter
depending on the values of the fields involved.
The potentially most interesting cause of isocurvature perturbations
is multiple dynamical fields in inflation. The fields will exchange
energy during inflation, and the field values will vary stochastically
between different points in space at the end of the phase transition,
generically giving isocurvature along with adiabatic perturbations
(Polarski and
Starobinsky 1994).
The numerical problem of setting initial conditions is somewhat
tricky. The general problem of evolving perturbations involves linear
evolution equations for around a dozen variables, outlined in
Sec. 3.2. Setting the correct
initial conditions involves specifying the value of each variable in
the limit as  ->
0. This is difficult for two reasons:
the equations are singular in this limit, and the equations become
increasingly numerically stiff in this limit. Simply using the
leading-order asymptotic behavior for all of the variables is only
valid in the high-temperature limit. Since the equations are stiff, small
departures from this limiting behavior
in any of the variables can lead to numerical instability until
the equations evolve to a stiff solution, and this numerical solution
does not necessarily correspond to the desired initial
conditions. Numerical techniques for setting the initial conditions to high
accuracy at temperaturesare currently being developed.
->
0. This is difficult for two reasons:
the equations are singular in this limit, and the equations become
increasingly numerically stiff in this limit. Simply using the
leading-order asymptotic behavior for all of the variables is only
valid in the high-temperature limit. Since the equations are stiff, small
departures from this limiting behavior
in any of the variables can lead to numerical instability until
the equations evolve to a stiff solution, and this numerical solution
does not necessarily correspond to the desired initial
conditions. Numerical techniques for setting the initial conditions to high
accuracy at temperaturesare currently being developed.
The characteristic ``acoustic peaks'' which appear in Figure 1 arise
from acoustic oscillations which are phase coherent:
at some point in time, the phases of all of the acoustic oscillations
were the same. This requires the same initial
condition for all k-modes, including those with wavelengths
longer than the horizon. Such a condition arises naturally for
inflationary models, but is very hard to reproduce in models producing
perturbations causally on scales smaller than the horizon. Defect
models, for example, produce acoustic oscillations, but the
oscillations generically have incoherent phases and thus display no
peak structure in their power spectrum
(Seljak et
al. 1997).
Simple models of inflation which produce only adiabatic perturbations
insure that all perturbations have the same phase at
 = 0 because
all of the perturbations are in the cosine mode of Eq. (28).
= 0 because
all of the perturbations are in the cosine mode of Eq. (28).
A glance at the k dependence of the adiabatic perturbation mode reveals how the coherent peaks are produced. The microwave background images the radiation density at a fixed time; as a function of k, the density varies like cos(krs), where rs is fixed. Physically, on scales much larger than the horizon at decoupling, a perturbation mode has not had enough time to evolve. At a particular smaller scale, the perturbation mode evolves to its maximum density in potential wells, at which point decoupling occurs. This is the scale reflected in the first acoustic peak in the power spectrum. Likewise, at a particular still smaller scale, the perturbation mode evolves to its maximum density in potential wells and then turns around, evolving to its minimum density in potential wells; at that point, decoupling occurs. This scale corresponds to that of the second acoustic peak. (Since the power spectrum is the square of the temperature fluctuation, both compressions and rarefactions in potential wells correspond to peaks in the power spectrum.) Each successive peak represents successive oscillations, with the scales of odd-numbered peaks corresponding to those perturbation scales which have ended up compressed in potential wells at the time of decoupling, while the even-numbered peaks correspond to the perturbation scales which are rarefied in potential wells at decoupling. If the perturbations are not phase coherent, then the phase of a given k-mode at decoupling is not well defined, and the power spectrum just reflects some mean fluctuation power at that scale.
In practice, two additional effects must be considered: a given scale in k-space is mapped to a range of l-values; and radiation velocities as well as densities contribute to the power spectrum. The first effect broadens out the peaks, while the second fills in the valleys between the peaks since the velocity extrema will be exactly out of phase with the density extrema. The amplitudes of the peaks in the power spectrum are also suppressed by Silk damping, as mentioned in Sec. 3.5.
The mass of the baryons creates a distinctive signature in the
acoustic oscillations
(Hu and Sugiyama
1996).
The zero-point of the oscillations is obtained
by setting 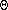 0
constant in Eq. (27): the result is
0
constant in Eq. (27): the result is

| (30) |
The photon temperature
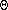 0 is not itself
observable, but must
be combined with the gravitational redshift to form the ``apparent
temperature''
0 is not itself
observable, but must
be combined with the gravitational redshift to form the ``apparent
temperature''
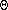 0 -
0 -
 , which oscillates around
a
, which oscillates around
a .
If the oscillation amplitude is much larger than
a
.
If the oscillation amplitude is much larger than
a  =
3
=
3 b
b
 /
4
/
4
 , then the
oscillations are effectively about
the mean temperature. The positive and negative oscillations are of
the same amplitude, so when the apparent temperature is squared to form the
power spectrum, all of the peaks have the same height. On the other
hand, if the baryons contribute a significant mass so that
a
, then the
oscillations are effectively about
the mean temperature. The positive and negative oscillations are of
the same amplitude, so when the apparent temperature is squared to form the
power spectrum, all of the peaks have the same height. On the other
hand, if the baryons contribute a significant mass so that
a is
a significant fraction of the oscillation amplitude, then the zero
point of the oscillations are displaced, and when the apparent
temperature is squared to form the power spectrum, the peaks arising
from the positive oscillations are higher than the peaks from the
negative oscillations. If
a
is
a significant fraction of the oscillation amplitude, then the zero
point of the oscillations are displaced, and when the apparent
temperature is squared to form the power spectrum, the peaks arising
from the positive oscillations are higher than the peaks from the
negative oscillations. If
a is larger than the
amplitude of the
oscillations, then the power spectrum peaks corresponding to the
negative oscillations disappear entirely. The physical interpretation
of this effect is that the baryon mass deepens the potential well in
which the baryons are oscillating, increasing the compression of the
plasma compared to the case with less baryon mass. In short, as the baryon
density increases, the power spectrum peaks corresponding to
compressions in potential wells get higher, while the alternating
peaks corresponding to rarefactions get lower. This alternating peak
height signature is a distinctive signature of baryon mass, and allows
the precise determination of the cosmological baryon density with the
measurement of the first several acoustic peak heights.
is larger than the
amplitude of the
oscillations, then the power spectrum peaks corresponding to the
negative oscillations disappear entirely. The physical interpretation
of this effect is that the baryon mass deepens the potential well in
which the baryons are oscillating, increasing the compression of the
plasma compared to the case with less baryon mass. In short, as the baryon
density increases, the power spectrum peaks corresponding to
compressions in potential wells get higher, while the alternating
peaks corresponding to rarefactions get lower. This alternating peak
height signature is a distinctive signature of baryon mass, and allows
the precise determination of the cosmological baryon density with the
measurement of the first several acoustic peak heights.