


2.2 The Poisson Distribution
The Poisson distribution occurs as the limiting form of the binomial
distribution when the probability p -> 0 and the number of trials
N ->  ,
such that the mean µ = Np, remains finite. The
probability of
observing r events in this limit then reduces to
,
such that the mean µ = Np, remains finite. The
probability of
observing r events in this limit then reduces to
Like (12), the Poisson distribution is discrete. It essentially
describes processes for which the single trial probability of success
is very small but in which the number of trials is so large that there
is nevertheless a reasonable rate of events. Two important examples of
such processes are radioactive decay and particle reactions.
To take a concrete example, consider a typical radioactive source
such as 137Cs which has a half-life of 27 years. The probability per
unit time for a single nucleus to decay is then
Note that in (16), only the mean appears so that knowledge of N
and p is not always necessary. This is the usual case in experiments
involving radioactive processes or particle reactions where the mean
counting rate is known rather than the number of nuclei or particles
in the beam. In many problems also, the mean per unit dimension
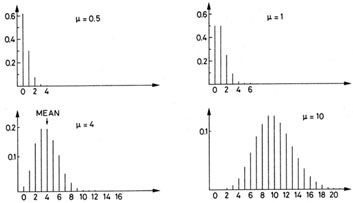
Fig. 2. Poisson distribution for various
values of µ.
An important feature of the Poisson distribution is that it depends
on only one parameter: µ. [That µ is indeed the
mean can be verified
by using (8)]. From (9), we also the find that
that is the variance of the Poisson distribution is equal to the mean.
The standard deviation is then
Figure 2 plots the Poisson distribution for
various values of µ.
Note that the distribution is not symmetric. The peak or maximum of
the distribution does not, therefore, correspond to the mean. However,
as µ becomes large, the distribution becomes more and more
symmetric
and approaches a Gaussian form. For µ
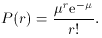
 = ln 2/27 =
0.026/year = 8.2 x 10-10 s-1. A small probability
indeed! However, even
a 1 µg sample of 137Cs will contain about
1015 nuclei. Since each
nucleus constitutes a trial, the mean number of decays from the sample
will be µ = Np = 8.2 x 105 decays/s. This
satisfies the limiting
conditions described above, so that the probability of observing r
decays is given by (16). Similar arguments can also be made for
particle scattering.
= ln 2/27 =
0.026/year = 8.2 x 10-10 s-1. A small probability
indeed! However, even
a 1 µg sample of 137Cs will contain about
1015 nuclei. Since each
nucleus constitutes a trial, the mean number of decays from the sample
will be µ = Np = 8.2 x 105 decays/s. This
satisfies the limiting
conditions described above, so that the probability of observing r
decays is given by (16). Similar arguments can also be made for
particle scattering.
 ,
e.g. the number of reactions per second, is specified and it is
desired to know the probability of observing r events in t
units, for
example, t = 3 s. An important point to note is that the mean in
(16) refers to the mean number in t units. Thus, µ =
,
e.g. the number of reactions per second, is specified and it is
desired to know the probability of observing r events in t
units, for
example, t = 3 s. An important point to note is that the mean in
(16) refers to the mean number in t units. Thus, µ =
 t. In these
types of problems we can rewrite (16) as
t. In these
types of problems we can rewrite (16) as
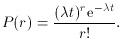
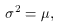
 =
=  µ. This explains
the use of the square roots in counting experiments.
µ. This explains
the use of the square roots in counting experiments.
 20, a Gaussian distribution
with mean µ and variance
20, a Gaussian distribution
with mean µ and variance
 2 = µ,
in fact, becomes a relatively good
approximation and can be used in place of the Poisson for numerical
calculations. Again, one must neglect the fact that we are replacing a
discrete distribution by a continuous one.
2 = µ,
in fact, becomes a relatively good
approximation and can be used in place of the Poisson for numerical
calculations. Again, one must neglect the fact that we are replacing a
discrete distribution by a continuous one.