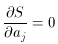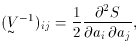7.1 The Least Squares Method
Let us suppose that measurements at n points,
xi, are made of the
variable yi with an error
i (i =
1, 2, . . ., n), and that it is desired
to fit a function f(x; a1,
a1, . . ., am) to these data where
a1, a1, . . .,
am, are unknown parameters to be determined. Of
course, the number of
points must be greater than the number of parameters. The method of
least squares states that the best values of aj are
those for which the sum
is a minimum. Examining (70) we can see that this is just the sum of
the squared deviations of the data points from the curve
f(xi)
weighted by the respective errors on yi. The reader
might also
recognize this as the chi-square in (22). for this reason, the
method is also sometimes referred to as chi-square
minimization. Strictly speaking this is not quite correct as
yi must
be Gaussian distributed with mean f(xi;
aj) and variance
To find the values of aj, one must now solve the
system of equations
Depending on the function f(x), (71) may or may not yield on
analytic solution. In general, numerical methods requiring a computer
must be used to minimize S.
Assuming we have the best values for aj, it is
necessary to estimate
the errors on the parameters. For this, we form the so-called
covariance or error matrix, Vij,
where the second derivative is evaluated at the minimum. (Note the
second derivatives form the inverse of the error matrix). The diagonal
elements Vij can then be shown to be the variances for
ai, while the
off-diagonal elements Vij represent the covariances
between ai and aj.
Thus,
and so on.
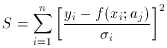
i2 in order
for S to be a true chi-square. However, as this is almost always the
case for measurements in physics, this is a valid hypothesis most of
the time. The least squares method, however, is totally general and
does not require knowledge of the parent distribution. If the parent
distribution is known the method of maximum likelihood may also be
used. In the case of Gaussian distributed errors this yields identical
results.
