7.3 Linear Fits When Both Variables Have Errors

In the previous examples, it was assumed that the independent variables x_i were completely free of errors. Strictly speaking, of course, this is never the case, although in many problems the errors on x are small with respect to those on y so that they may be neglected. In cases where the errors on both variables are comparable, however, ignoring the errors on x leads to incorrect parameters and an underestimation of their errors. For these problems the effective variance method may be used. Without deriving the result which is discussed by Lybanon [Ref. 7] and Orear [Ref. 8] for Gaussian distributed errors, the method consists of simply replacing the variance _i² in (70) by

(84)

where 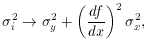_x and _y, are the errors on x and y respectively. Since the derivative is normally a function of the parameters a_j, S is nonlinear and numerical methods must be used to minimize S.