4. FRAGMENTATION OF THE FIRST GASEOUS OBJECTS

4.1. Star Formation

4.1.1. Fragmentation into Stars

As mentioned in the preface, the fragmentation of the first gaseous objects is a well-posed physics problem with well specified initial conditions, for a given power-spectrum of primordial density fluctuations. This problem is ideally suited for three-dimensional computer simulations, since it cannot be reliably addressed in idealized 1D or 2D geometries.

Recently, two groups have attempted detailed 3D simulations of the formation process of the first stars in a halo of ~ 10⁶ M by following the dynamics of both the dark matter and the gas components, including H₂ chemistry and cooling (Deuterium is not expected to play a significant role; Bromm 2000). Bromm et al. (1999) have used a Smooth Particle Hydrodynamics (SPH) code to simulate the collapse of a top-hat overdensity with a prescribed solid-body rotation (corresponding to a spin parameter = 5%) and additional small perturbations with P(k) k^-3 added to the top-hat profile. Abel et al. (2000) isolated a high-density filament out of a larger simulated cosmological volume and followed the evolution of its density maximum with exceedingly high resolution using an Adaptive Mesh Refinement (AMR) algorithm.

The generic results of Bromm et al. (1999; see also Bromm 2000) are illustrated in Figure 13. The collapsing region forms a disk which fragments into many clumps. The clumps have a typical mass ~ 10²-10³ M. This mass scale corresponds to the Jeans mass for a temperature of ~ 500K and the density ~ 10⁴ cm^-3 where the gas lingers because its cooling time is longer than its collapse time at that point (see Figure 14). This characteristic density is determined by the fact that hydrogen molecules reach local thermodynamic equilibrium at this density. At lower densities, each collision leads to an excited state and to radiative cooling, so the overall cooling rate is proportional to the collision rate, and the cooling time is inversely proportional to the gas density. Above the density of ~ 10⁴ cm^-3, however, the relative occupancy of each excited state is fixed at the thermal equilibrium value (for a given temperature), and the cooling time is nearly independent of density (e.g., Lepp & Shull 1983). Each clump accretes mass slowly until it exceeds the Jeans mass and collapses at a roughly constant temperature (i.e., isothermally) due to H₂ cooling. The clump formation efficiency is high in this simulation due to the synchronized collapse of the overall top-hat perturbation.

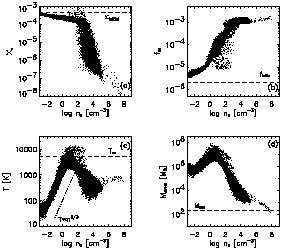
Figure 13. Numerical results from Bromm et al. (1999), showing gas properties at z = 31.2 for a collapsing slightly inhomogeneous top-hat region with a prescribed solid-body rotation. Each point in the figure is a gas particle in the simulation. (a) Free electron fraction (by number) vs. hydrogen number density (in cm-3). At densities exceeding n ~ 103 cm-3, recombination is very efficient, and the gas becomes almost completely neutral. (b) Molecular hydrogen fraction vs. number density. After a quick initial rise, the H2 fraction approaches the asymptotic value of f ~ 10-3, due to the H- channel. (c) Gas temperature vs. number density. At densities below ~ 1 cm-3, the gas temperature rises because of adiabatic compression until it reaches the virial value of Tvir 5000 K. At higher densities, cooling due to H2 drives the temperature down again, until the gas settles into a quasi-hydrostatic state at T ~ 500 K and n ~ 104 cm-3. Upon further compression due to accretion and the onset of gravitational collapse, the gas shows a further modest rise in temperature. (d) Jeans mass (in M) vs. number density. The Jeans mass reaches a value of MJ ~ 103 M for the quasi-hydrostatic gas in the center of the potential well, and reaches the resolution limit of the simulation, Mres 200 M, for densities close to n = 108 cm-3.

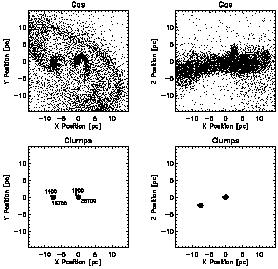
Figure 14. Gas and clump morphology at z = 28.9 in the simulation of Bromm et al. (1999). Top row: The remaining gas in the diffuse phase. Bottom row: Distribution of clumps. The numbers next to the dots denote clump mass in units of M. Left panels: Face-on view. Right panels: Edge-on view. The length of the box is 30 pc. The gas has settled into a flattened configuration with two dominant clumps of mass close to 20, 000M. During the subsequent evolution, the clumps survive without merging, and grow in mass only slightly by accretion of surrounding gas.

Bromm (2000, Chapter 7) has simulated the collapse of one of the above-mentioned clumps with ~ 1000 M and demonstrated that it does not tend to fragment into sub-components. Rather, the clump core of ~ 100 M free-falls towards the center leaving an extended envelope behind with a roughly isothermal density profile. At very high gas densities, three-body reactions become important in the chemistry of H₂. Omukai & Nishi (1999) have included these reactions as well as radiative transfer and followed the collapse in spherical symmetry up to stellar densities. Radiation pressure from nuclear burning at the center is unlikely to reverse the infall as the stellar mass builds up. These calculations indicate that each clump may end up as a single massive star; however, it is possible that angular momentum or nuclear burning may eventually halt the monolithic collapse and lead to further fragmentation.

The Jeans mass (Section 3.1), which is defined based on small fluctuations in a background of uniform density, does not strictly apply in the context of collapsing gas cores. We can instead use a slightly modified critical mass known as the Bonnor-Ebert mass (Bonnor 1956; Ebert 1955). For baryons in a background of uniform density _b, perturbations are unstable to gravitational collapse in a region more massive than the Jeans mass

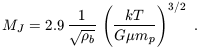
(52)

Instead of a uniform background, we consider a spherical, non-singular, isothermal, self-gravitating gas in hydrostatic equilibrium, i.e., a centrally-concentrated object which more closely resembles the gas cores found in the above-mentioned simulations. We consider a finite sphere in equilibrium with an external pressure. In this case, small fluctuations are unstable and lead to collapse if the sphere is more massive than the Bonnor-Ebert mass M_BE, given by the same expression as equation (52) but with a different coefficient (1.2 instead of 2.9) and with _b denoting in this case the gas (volume) density at the surface of the sphere.

In their simulation, Abel et al. (2000) adopted the actual cosmological density perturbations as initial conditions. The simulation focused on the density peak of a filament within the IGM, and evolved it to very high densities (Figure 15). Following the initial collapse of the filament, a clump core formed with ~ 200 M, amounting to only ~ 1% of the virialized gas mass. Subsequently due to slow cooling, the clump collapsed subsonically in a state close to hydrostatic equilibrium (see Figure 16). Unlike the idealized top-hat simulation of Bromm et al. (2000), the collapse of the different clumps within the filament is not synchronized. Once the first star forms at the center of the first collapsing clump, it is likely to affect the formation of other stars in its vicinity.

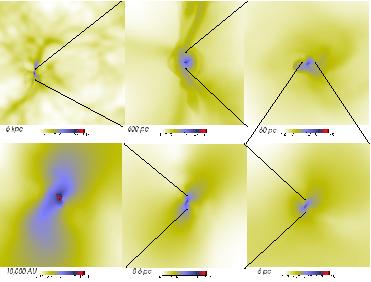
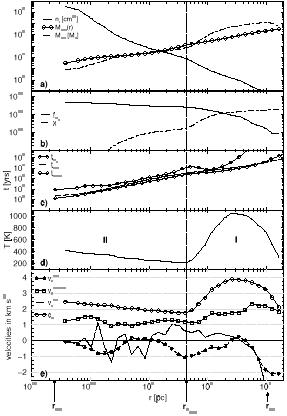
Figure 15. Zooming in on the core of a star forming region with the Adaptive Mesh Refinement simulation of Abel et al. (2000). The panels show different length scales, decreasing clockwise by an order of magnitude between adjacent panels. Note the large dynamic range of scales which are being resolved, from 6 kpc (top left panel) down to 10,000 AU (bottom left panel).

Figure 16. Gas profiles from the simulation of Abel et al. (2000). The cell size on the finest grid corresponds to 0.024 pc, while the simulation box size corresponds to 6.4 kpc. Shown are spherically-averaged mass-weighted profiles around the baryon density peak shortly before a well defined fragment forms (z = 19.1). Panel (a) shows the baryonic number density (solid line), enclosed gas mass in solar mass (thin solid line with circles), and the local Bonnor-Ebert mass MBE (dashed line; see text). Panel (b) plots the molecular hydrogen fraction (by number) fH2 (solid line) and the free electron fraction x (dashed line). The H2 cooling time, tH2, the time it takes a sound wave to travel to the center, tcross, and the free-fall time tff = [3 / (32 G ]1/2 are given in panel (c). Panel (d) gives the temperature in K as a function of radius. The bottom panel gives the local sound speed, cs (solid line with circles), the root-mean-square radial velocities of the dark matter (dashed line) and the gas (dashed line with asterisks) as well as the root-mean-square gas velocity (solid line with square symbols). The vertical dotted line indicates the radius (~ 5 pc) at which the gas has reached its minimum temperature allowed by H2 cooling. The virial radius of the 5.6 × 106 M halo is 106 pc.

If the clumps in the above simulations end up forming individual very massive stars, then these stars will likely radiate copious amounts of ionizing radiation (Carr, Bond, & Arnett 1984; Tumlinson & Shull 2000; Bromm et al. 2000) and expel strong winds. Hence, the stars will have a large effect on their interstellar environment, and feedback is likely to control the overall star formation efficiency. This efficiency is likely to be small in galactic potential wells which have a virial temperature lower than the temperature of photoionized gas, ~ 10⁴K. In such potential wells, the gas may go through only a single generation of star formation, leading to a ``suicidal'' population of massive stars.

The final state in the evolution of these stars is uncertain; but if their mass loss is not too extensive, then they are likely to end up as black holes (Bond, Carr, & Arnett 1984; Fryer, Woosley, & Heger 2000). The remnants may provide the seeds of quasar black holes (Larson 1999). Some of the massive stars may end their lives by producing -ray bursts. If so then the broad-band afterglows of these bursts could provide a powerful tool for probing the epoch of reionization (Lamb & Reichart 2000; Ciardi & Loeb 2000). There is no better way to end the dark ages than with -ray burst fireworks.

Where are the first stars or their remnants located today? The very first stars formed in rare high- peaks and hence are likely to populate the cores of present-day galaxies (White & Springel 1999). However, the star clusters which formed in low- peaks at later times are expected to behave similarly to the collisionless dark matter particles and populate galaxy halos (Loeb 1998).

4.1.2. Emission Spectrum of Metal-Free Stars

The evolution of metal-free (Population III) stars is qualitatively different from that of enriched (Population I and II) stars. In the absence of the catalysts necessary for the operation of the CNO cycle, nuclear burning does not proceed in the standard way. At first, hydrogen burning can only occur via the inefficient PP chain. To provide the necessary luminosity, the star has to reach very high central temperatures (T_c 10^8.1 K). These temperatures are high enough for the spontaneous turn-on of helium burning via the triple- process. After a brief initial period of triple- burning, a trace amount of heavy elements forms. Subsequently, the star follows the CNO cycle. In constructing main-sequence models, it is customary to assume that a trace mass fraction of metals (Z ~ 10^-9) is already present in the star (El Eid et al. 1983; Castellani et al. 1983).

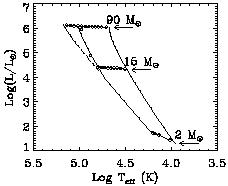
Figures 17 and 18 show the luminosity L vs. effective temperature T for zero-age main sequence stars in the mass ranges of 2-90 M (Figure 17) and 100-1000 M (Figure 18). Note that above ~ 100 M the effective temperature is roughly constant, T_eff ~ 10⁵K, implying that the spectrum is independent of the mass distribution of the stars in this regime (Bromm et al. 2000). As is evident from these Figures (see also Tumlinson & Shull 2000), both the effective temperature and the ionizing power of metal-free (Pop III) stars are substantially larger than those of metal-rich (Pop I) stars. Metal-free stars with masses 20 M emit between 10⁴⁷ and 10⁴⁸ H1 and He1 ionizing photons per second per solar mass of stars, where the lower value applies to stars of ~ 20 M and the upper value applies to stars of 100 M (see Tumlinson & Shull 2000 and Bromm et al. 2000 for more details). These massive stars produce 10⁴-10⁵ ionizing photons per stellar baryon over a lifetime of ~ 3 × 10⁶ years [which is much shorter than the age of the universe, equation (10) in Section 2.1]. However, this powerful UV emission is suppressed as soon as the interstellar medium out of which new stars form is enriched by trace amounts of metals. Even though the collapsed fraction of baryons is small at the epoch of reionization, it is likely that most of the stars responsible for the reionization of the universe formed out of enriched gas.

Figure 17. Luminosity vs. effective temperature for zero-age main sequences stars in the mass range of 2-90 M (from Tumlinson & Shull 2000). The curves show Pop I (Z = 0.02, on the right) and Pop III stars (on the left) in the mass range 2-90 M. The diamonds mark decades in metallicity in the approach to Z = 0 from 10-2 down to 10-5 at 2 M, down to 10-10 at 15 M, and down to 10-13 at 90 M. The dashed line along the Pop III zero-age main sequence assumes pure H-He composition, while the solid line (on the left) marks the upper MS with ZC = 10-10 for the M 15 M models. Squares mark the points corresponding to pre-enriched evolutionary models from El Eid et al. (1983) at 80 M and from Castellani et al. (1983) at 25 M.

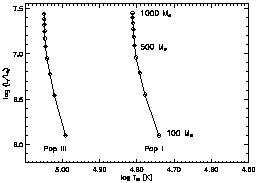
Figure 18. Same as Figure 17 but for very massive stars above 100 M (from Bromm et al. 2000). Left solid line: Pop III zero-age main sequence (ZAMS). Right solid line: Pop I ZAMS. In each case, stellar luminosity (in L) is plotted vs. effective temperature (in K). Diamond-shaped symbols: Stellar masses along the sequence, from 100M (bottom) to 1000M (top) in increments of 100M. The Pop III ZAMS is systematically shifted to higher effective temperature, with a value of ~ 105 K which is approximately independent of mass. The luminosities, on the other hand, are almost identical in the two cases.

Will it be possible to infer the initial mass function (IMF) of the first stars from spectroscopic observations of the first galaxies? Figure 19 compares the observed spectrum from a Salpeter IMF (dN_* / dM M^-2.35) and a heavy IMF (with all stars more massive than 100 M) for a galaxy at z_s = 10. The latter case follows from the assumption that each of the dense clumps in the simulations described in the previous section ends up as a single star with no significant fragmentation or mass loss. The difference between the plotted spectra cannot be confused with simple reddening due to normal dust. Another distinguishing feature of the IMF is the expected flux in the hydrogen and helium recombination lines, such as Ly and He II 1640 Å, from the interstellar medium surrounding these stars. We discuss this next.

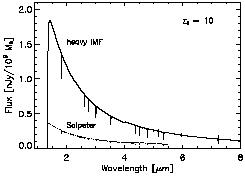
Figure 19. Comparison of the predicted flux from a Pop III star cluster at zs = 10 for a Salpeter IMF (Tumlinson & Shull 2000) and a massive IMF (Bromm et al. 2000). Plotted is the observed flux (in nJy per 106 M of stars) vs. observed wavelength (in µm) for a flat universe with = 0.7 and h = 0.65. Solid line: The case of a heavy IMF. Dotted line: The fiducial case of a standard Salpeter IMF. The cutoff below obs = 1216 Å (1 + zs) = 1.34µm is due to Gunn-Peterson absorption. (The cutoff has been slightly smoothed here by the damping wing of the Ly line, with reionization assumed to occur at z = 7; see Section 9.1.1 for details.) Clearly, for the same total stellar mass, the observable flux is larger by an order of magnitude for stars which are biased towards having masses 100 M .

4.1.3. Emission of Recombination Lines from the First Galaxies

The hard UV emission from a star cluster or a quasar at high redshift is likely reprocessed by the surrounding interstellar medium, producing very strong recombination lines of hydrogen and helium (Oh 1999; Tumlinson & Shull 2000; see also Baltz, Gnedin & Silk 1998). We define 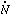_ion to be the production rate per unit stellar mass of ionizing photons by the source. The emitted luminosity L_line^em per unit stellar mass in a particular recombination line is then estimated to be

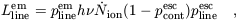
(53)

where p_line^em is the probability that a recombination leads to the emission of a photon in the corresponding line, is the frequency of the line and p^esc_cont and p^esc_line are the escape probabilities for the ionizing photons and the line photons, respectively. It is natural to assume that the stellar cluster is surrounded by a finite H II region, and hence that p^esc_cont is close to zero (Wood & Loeb 2000; Ricotti & Shull 2000). In addition, p^esc_line is likely close to unity in the H II region, due to the lack of dust in the ambient metal-free gas. Although the emitted line photons may be scattered by neutral gas, they diffuse out to the observer and in the end survive if the gas is dust free. Thus, for simplicity, we adopt a value of unity for p^esc_line (two-photon decay is generally negligible as a way of losing line photons in these environments).

As a particular example we consider case B recombination which yields p_line^em of about 0.65 and 0.47 for the Ly and He II 1640Å lines, respectively. These numbers correspond to an electron temperature of ~ 3 × 10⁴K and an electron density of ~ 10² - 10³ cm^-3 inside the H II region (Storey & Hummer 1995). For example, we consider the extreme and most favorable case of metal-free stars all of which are more massive than ~ 100 M. In this case L_line^em = 1.7 × 10³⁷ and 2.2 × 10³⁶ erg s^-1 M^-1 for the recombination luminosities of Ly and He II 1640Å per stellar mass (Bromm et al. 2000). A cluster of 10⁶ M in such stars would then produce 4.4 and 0.6 × 10⁹ L in the Ly and He II 1640Å lines. Comparably-high luminosities would be produced in other recombination lines at longer wavelengths, such as He II 4686Å and H (Oh 2000; Oh, Haiman, & Rees 2000).

The rest-frame equivalent width of the above emission lines measured against the stellar continuum of the embedded star cluster at the line wavelengths is given by

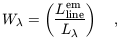
(54)

where L is the spectral luminosity per unit wavelength of the stars at the line resonance. The extreme case of metal-free stars which are more massive than 100 M yields a spectral luminosity per unit frequency L = 2.7 × 10²¹ and 1.8 × 10²¹ erg s^-1 Hz^-1 M^-1 at the corresponding wavelengths (Bromm et al. 2000). Converting to L, this yields rest-frame equivalent widths of W = 3100Å and 1100Å for Ly and He II 1640Å, respectively. These extreme emission equivalent widths are more than an order of magnitude larger than the expectation for a normal cluster of hot metal-free stars with the same total mass and a Salpeter IMF under the same assumptions concerning the escape probabilities and recombination (Kudritzki et al. 2000). The equivalent widths are, of course, larger by a factor of (1 + z_s) in the observer frame. Extremely strong recombination lines, such as Ly and He II 1640Å, are therefore expected to be an additional spectral signature that is unique to very massive stars in the early universe. The strong recombination lines from the first luminous objects are potentially detectable with NGST (Oh, Haiman, & Rees 2000).

High-redshift objects could also, in principle, be detected through their cooling radiation. However, a simple estimate of the radiated energy shows that it is very difficult to detect the corresponding signal in practice. As it cools, the gas loses much of its gravitational binding energy, which is of order k_BT_vir per baryon, with the virial temperature given by equation (26) in Section 2.3. Some fraction of this energy is then radiated as Ly photons. The typical galaxy halos around the reionization redshift have T_vir ~ 1 eV, and this must be compared to the nuclear energy output of 7 MeV per baryon in stellar interiors. Clearly, for a star formation efficiency of 1%, the stellar radiation is expected to be far more energetic than the cooling radiation. Both forms of energy should come out on a time-scale of order the dynamical time. Thus, even if the cooling radiation is concentrated in the Ly line, its detection is more promising for low redshift objects, while NGST will only be able to detect this radiation from the rare 4- halos (with masses 10¹1 M) at z ~ 10 (Haiman, Spaans, & Quataert 2000; Fardal et al. 2000).

4.2. Black Hole Formation

Quasars are more effective than stars in ionizing the intergalactic hydrogen because (i) their emission spectrum is harder, (ii) the radiative efficiency of accretion flows can be more than an order of magnitude higher than the radiative efficiency of a star, and (iii) quasars are brighter, and for a given density distribution in their host system, the escape fraction of their ionizing photons is higher than for stars.

Thus, the history of reionization may have been greatly altered by the existence of massive black holes in the low-mass galaxies that populate the universe at high redshifts. For this reason, it is important to understand the formation of massive black holes (i.e., black holes with a mass far greater than a stellar mass). The problem of black hole formation is not a priori more complicated than the problem of star formation. Surprisingly, however, the amount of theoretical work on star formation far exceeds that on massive black hole formation. One of the reasons is that stars form routinely in our interstellar neighborhood where much data can be gathered, while black holes formed mainly in the distant past at great distances from our telescopes. As more information is gathered on the high-redshift universe, this state of affairs may begin to change.

Here we adopt the view that massive black holes form out of gas and not through the dynamical evolution of dense stellar systems (see Rees 1984 for a review of the alternatives). To form a black hole inside a given dark matter halo, the baryons must cool. For most objects, this is only possible with atomic line cooling at virial temperatures T_vir 10⁴K and thus baryonic masses 10⁷ M[(1 + z) / 10]^3/2. After losing their thermal pressure, the cold baryons collapse and form a thin disk on a dynamical time (Loeb & Rasio 1994). The basic question is then the following: what fraction of the cold baryons is able to sink to the very center of the potential well and form a massive black hole? Just as for star formation, the main barrier in this process is angular momentum. The centrifugal force opposes radial infall and keeps the gas in disks at a typical distance which is 6-8 orders of magnitude larger than the Schwarzschild radius corresponding to the total gas mass. Eisenstein & Loeb (1995b) demonstrated that a small fraction of all objects have a sufficiently low angular momentum that the gas in them inevitably forms a compact semi-relativistic disk that evolves to a black hole on a short viscous time-scale. These low-spin systems are born in special cosmological environments that exert unusually small tidal torques on them during their cosmological collapse. As long as the initial cooling time of the gas is short and its star formation efficiency is low, the gas forms the compact disk on a free-fall time. In most systems the baryons dominate gravity inside the scale length of the disk. Therefore, if the baryons in a low-spin system acquire a spin parameter which is only one sixth of the typical value, i.e., an initial rotation speed ~ (16% × 0.05) × V_c, then with angular momentum conservation they would reach rotational support at a radius r_disk and circular velocity V_disk such that V_disk r_disk ~ (16% × 0.05) V_c r_vir, where r_vir is the virial radius and V_c the circular velocity of the halo. Using the relations: (G M_halo / r_vir) ~ V_c², and [G(_b / _m M_halo / r_disk] ~ V_disk², we get V_disk ~ 18V_c. For T_vir ~ 10⁴K, the dark matter halo has a potential depth corresponding to a circular velocity of V_c ~ 17 km s^-1, and the low-spin disk attains a characteristic rotation velocity of V_disk ~ 300 km s^-1 (sufficient to retain the gas against supernova-driven winds), a size 1 pc, and a viscous evolution time which is extremely short compared to the Hubble time.

Low-spin dwarf galaxies populate the universe with a significant volume density at high redshift; these systems are eventually incorporated into higher mass galaxies which form later. For example, a galactic bulge of ~ 10¹⁰ M in baryons forms out of ~ 10³ building blocks of ~ 10⁷ M each. In order to seed the growth of a quasar, it is sufficient that only one of these systems had formed a low-spin disk that produced a black hole progenitor. Note that if a low-spin object is embedded in an overdense region that eventually becomes a galactic bulge, then the black hole progenitor will sink to the center of the bulge by dynamical friction in less than a Hubble time (for a sufficiently high mass 10⁶ M ; p. 428 of Binney & Tremaine) and seed quasar activity. Based on the phase-space volume accessible to low-spin systems ( j³), we expect a fraction ~ 6^-3 = 5 × 10^-3 of all the collapsed gas mass in the universe to be associated with low-spin disks (Eisenstein & Loeb 1995b). However, this is a conservative estimate. Additional angular momentum loss due to dynamical friction of gaseous clumps in dark matter halos (Navarro, Frenk, & White 1995) or bar instabilities in self-gravitating disks (Shlosman, Begelman, & Frank 1990) could only contribute to the black hole formation process. The popular paradigm that all galaxies harbor black holes at their center simply postulates that in all massive systems, a small fraction of the gas ends up as a black hole, but does not explain quantitatively why this fraction obtains its particular small value. The above scenario offers a possible physical context for this result.

If the viscous evolution time is shorter than the cooling time and if the gas entropy is raised by viscous dissipation or shocks to a sufficiently high value, then the black hole formation process will go through the phase of a supermassive star (Shapiro & Teukolsky 1983, Section 17; see also Zel'dovich & Novikov 1971). The existence of angular momentum (Wagoner 1969) tends to stabilize the collapse against the instability which itself is due to general-relativistic corrections to the Newtonian potential (Shapiro & Teukolsky 1983, Section 17.4). However, shedding of mass and angular momentum along the equatorial plane eventually leads to collapse (Bisnovati-Kogan, Zel'dovich & Novikov 1967; Loeb & Rasio 1994; Baumgarte & Shapiro 1999a). Since it is convectively unstable (Loeb & Rasio 1994) and supported by radiation pressure, a supermassive star should radiate close to the Eddington limit (with modifications due to rotation; see Baumgarte & Shapiro 1999b) and generate a strong wind, especially if the gas is enriched with metals. The thermal+wind emission associated with the collapse of a supermassive star should be short-lived and could account for only a minority of all observed quasars.

After the seed black hole forms, it is continually fed with gas during mergers. Mihos & Hernquist (1996) have demonstrated that mergers tend to deposit large quantities of gas at the centers of the merging galaxies, a process which could fuel a starburst or a quasar. If both of the merging galaxies contain black holes at their centers, dynamical friction will bring the black holes together. The final spiral-in of the black hole binary depends on the injection of new stars into orbits which allow them to extract angular momentum from the binary (Begelman, Blandford, & Rees 1980). If the orbital radius of the binary shrinks to a sufficiently small value, gravitational radiation takes over and leads to coalescence of the two black holes. This will provide powerful sources for future gravitational wave detectors (such as the LISA project; see http://lisa.jpl.nasa.gov).

The fact that black holes are found in low-mass galaxies in the local universe implies that they are likely to exist also at high redshift. Local examples include the compact ellipticals M32 and NGC 4486B. In particular, van der Marel et al. (1997) infer a black hole mass of ~ 3.4 × 10⁶ M in M32, which is a fraction ~ 8 × 10^-3 of the stellar mass of the galaxy, ~ 4 × 10⁸ M, for a central mass-to-light ratio of _V = 2. In NGC 4486B, Kormendy et al. (1997) infer a black hole mass of 6 × 10⁸ M, which is a fraction ~ 9% of the stellar mass.

Despite the poor current understanding of the black hole formation process, it is possible to formulate reasonable phenomenological prescriptions that fit the quasar luminosity function within the context of popular galaxy formation models. These prescription are described in Section 8.2.2.