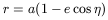
| (64) |
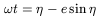
| (65) |



Globular clusters and satellite galaxies are stellar components at large distances from the centre and are therefore ideal probes of the gravitational potential of a galaxy. The Milky Way may constitute, once more, the best example. Actually, globular clusters are typically at distances of less than 10 kpc, much lower than typical halo sizes, and are therefore not so suitable. Satellite galaxies are further away but they are statistically scarce, probably only nine satellites belonging to our Galaxy. However, satellites are also observable in other galaxies.
Suppose a Keplerian potential - GM/r and that, therefore, for satellites with elliptical orbits
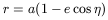
| (64) |
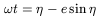
| (65) |
as in 3.5.1. Time derivatives are
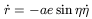
| (66) |
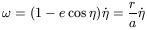
| (67) |
Therefore
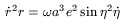
| (68) |
Let us calculate the mean time value of this quantity during a complete orbit
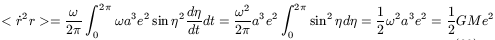
| (69) |
Therefore, the galactic mass M could be obtained from the quantity
< ![]() r >. If we now consider not a single
cluster or satellite but an
assemblage of them in a given time, the mean time value would not differ
from the mean value of
r >. If we now consider not a single
cluster or satellite but an
assemblage of them in a given time, the mean time value would not differ
from the mean value of
![]() ri of the different clusters, at
present. We need to know the eccentricity, which would be different
for the different clusters. The mean-square value for isotropic orbits
is 1/2.
Binney and Tremaine (1987),
who have presented this argument, propose
ri of the different clusters, at
present. We need to know the eccentricity, which would be different
for the different clusters. The mean-square value for isotropic orbits
is 1/2.
Binney and Tremaine (1987),
who have presented this argument, propose
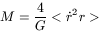
| (70) |
This method was applied by
Lynden-Bell et al. (1983),
who obtained
M = 3.8 × 1011M![]() with 9 satellites of the Milky Way
(both Magellanic Clouds, Leo I and II,
Fornax, Sculptor, Ursa Minor,
Draco and Carina).
with 9 satellites of the Milky Way
(both Magellanic Clouds, Leo I and II,
Fornax, Sculptor, Ursa Minor,
Draco and Carina).
The adoption of a Keplerian potential was not fully justified as 6 out
of the 9 selected satellites are at distances of less than 100 kpc, lower
than a
reasonable size of the dark matter halo. The unknown value of the
eccentricities is also a major source of errors. If the orbits were
radially elongated, with e = 1, the calculated mass would be closer
to the galactic mass deduced from the visible matter alone. That
orbits could be elongated rather than isotropic is somewhat suggested
by the fact that (with the exceptions of Leo I and Leo II, which are
too far away)
all the satellites of the Milky Way are roughly aligned in a line
connecting (
b = - 45o, l = 270o)
![]() (b = 45o, l = 90o).
(b = 45o, l = 90o).
Ashman (1992) and
Trimble (1987)
have summarized previous work carried out by
Little and Tremaine (1991),
Zaritsky et al. (1989),
Salucci and Frenk (1989),
Peterson and Latham (1989),
Kulessa and Lynden-Bell (1992)
and others. The results obtained by the different authors are
very different, depending on the inclusion or exclusion of some distant
satellites, in particular on the inclusion or exclusion of Leo I. However, a
mass of
1012M![]() and a halo radius of 100 kpc are typical
values.
and a halo radius of 100 kpc are typical
values.
This type of analysis will be more promising in the future, when proper
motions of the satellites of the Milky Way become available.
Wilkinson and Evans (1999)
have incorporated into the
computation the known proper motions of 6 satellites. They obtain a
value of about
2 × 1012M![]() for the mass of the Milky
Way, with the inclusion or exclusion of Leo I not being so important as
when only radial motions are considered. The results are model
dependent and these authors have chosen a peculiar one, called the
"truncated flat" rotation curve, in which the density decreases as
r-2 in the inner parts and decreases as r-5 in the outer ones.
for the mass of the Milky
Way, with the inclusion or exclusion of Leo I not being so important as
when only radial motions are considered. The results are model
dependent and these authors have chosen a peculiar one, called the
"truncated flat" rotation curve, in which the density decreases as
r-2 in the inner parts and decreases as r-5 in the outer ones.
Tidal radii (see Section 3.3) of globular
clusters and satellite galaxies have also been considered (e.g.
Innanen et al. 1983)
but these
radii are obtained by an extrapolation of the photometric data, which
introduces a lot of uncertainty. A mass of about
9 × 1011M![]() and a halo size of at least 44 kpc
were obtained by these authors.
and a halo size of at least 44 kpc
were obtained by these authors.
Satellites of other galaxies have been studied by
Zaritsky et al. (1993),
Zaritsky and White (1994),
Zaritsky (1997)
and others. The
problem has much in common with that of binary galaxies but presents
particular interest because, as satellites are supposed to be low mass
systems they can be considered as test particles orbiting in the total
mass of the primary. The above authors have observed 115 satellites
around 69
isolated primary galaxies. They conclude that DM halos do exist and
that they extend to distances of over 400 kpc, actually a
very large figure, but many characteristic facts are
difficult to explain: a) There is a complete lack of correlation
between ![]() v and
v and ![]() r, which impedes the obtention of the
mean value of galaxies. b) There is a complete lack of correlation
between
r, which impedes the obtention of the
mean value of galaxies. b) There is a complete lack of correlation
between ![]() v and the HI widths. It has been mentioned that
Salucci and Persic (1997)
and, as will be mentioned later,
theoretical models do not expect a large correlation between these
two quantities, but not a vanishing one, either. c) Satellites seem to be
preferentially distributed near the plane perpendicular to the rotation
axis of the primary. d) The assemblage of all the satellites seems to
present a "rotation curve" around a typical primary without signs of
becoming flat. Note that the possibility of a common DM halo
without an internal DM structure is a picture compatible with these
observations.
v and the HI widths. It has been mentioned that
Salucci and Persic (1997)
and, as will be mentioned later,
theoretical models do not expect a large correlation between these
two quantities, but not a vanishing one, either. c) Satellites seem to be
preferentially distributed near the plane perpendicular to the rotation
axis of the primary. d) The assemblage of all the satellites seems to
present a "rotation curve" around a typical primary without signs of
becoming flat. Note that the possibility of a common DM halo
without an internal DM structure is a picture compatible with these
observations.