Dark Energy and the Preposterous Universe

1. THE PREPOSTEROUS UNIVERSE

Surprising experimental results are the most common driving force behind significant advances in scientific understanding. The recent discovery that the universe appears to be dominated by a component of "dark energy" qualifies as an extraordinarily surprising result; we have every reason to be optimistic that attempts to understand this phenomenon will lead to profound improvements in our pictures of gravitation, particle physics, and gravitation.

1.1. Dark energy

In general relativity, a homogeneous and isotropic universe is characterized by two quantities, the spatial curvature kappa and scale factor a(t). These are related to the energy density $\rho$ by the Friedmann equation:

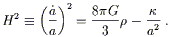
(1)

For any value of the Hubble expansion parameter H, there is a critical density which solves this equation for zero spatial curvature: $\rho_{\rm crit}^{}$ = 3H²/8 $\pi$ G. The energy density is conveniently characterized by a density parameter constructed by normalizing with respect to the critical density: $\Omega$ = $\rho$ / $\rho_{\rm crit}^{}$ .

Observations of the dynamics of galaxies and clusters have shown that the amount of ``matter'' (slowly-moving particles that can fall into local gravitational potential wells) is $\Omega_{\rm M}^{}$ = 0.3 ± 0.1, short of the critical density. At the same time, however, observations of temperature anisotropies in the cosmic microwave background (CMB) are consistent with nearly scale-free, gaussian, adiabatic primordial density perturbations (the kind predicted by the inflationary universe scenario) for a nearly spatially flat universe, $\Omega_{\rm total}^{}$ approx 1. We therefore infer the existence of a dark energy component $\rho_{\rm dark}^{}$ smoothly distributed through space (so that it does not influence the local motions of galaxies and clusters), with $\Omega_{\rm dark}^{}$ approx 0.7. (See [1] for a recent overview and references.)

Meanwhile, measurements of the distance vs. redshift relation for Type Ia supernovae [2, 3] have provided evidence that the universe is accelerating - that $\ddot{a}$ > 0. The significance of this discovery can be appreciated by rewriting the Friedmann equation (1) after multiplying by a²:

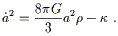
(2)

The energy density in matter (non-relativistic particles) diminishes as the number density is diluted by expansion, so that $\rho_{\rm M}^{}$ propto a^-3. If particles are relativistic, and thus classified as "radiation", they are both diluted in number density and have their individual energies redshift as a^-1, so that $\rho_{\rm R}^{}$ propto a^-4. For either of these conventional sources of energy density, the right-hand side of (2) will be decreasing in an expanding universe (since a² $\rho$ is decreasing, while kappa is a constant), so that $\dot{a}$ will be decreasing. The supernova data therefore imply that, to make the universe accelerate, the dark energy must be varying slowly with time (roughly speaking, redshifting away more slowly than a^-2) as well as with space.

There is a straightforward candidate for a dark energy component that varies slowly in both space and time: vacuum energy, or the cosmological constant (for reviews see [1, 4, 5, 6, 7, 8]). The distinguishing feature of vacuum energy is that it is a minimum amount of energy density in any region, strictly constant throughout spacetime. To match the data, we require a vacuum energy

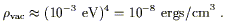
(3)

(In units where $\hbar$ = c = 1, energy density has units of [energy]⁴.) The idea that the dark energy density is simply a constant inherent in the fabric of spacetime is in excellent agreement with the data, but raises two very difficult questions: first, why is the vacuum energy so much smaller than what we would think of as its natural value (the cosmological constant problem); and second, why are the matter and vacuum energy densities approximately equal today (the coincidence problem)? Of course the first question is important even if the dark energy is not a cosmological constant, although a nonzero value for the vacuum energy makes its smallness perhaps even more puzzling than if it were simply zero.

1.2. The cosmological constant problem

Let us turn first to the issue of why the vacuum energy is smaller than we might expect. Although the notion that empty space has a nonzero energy density can seem surprising at first, it is a very natural occurrence in any generic pairing of general relativity with field theory (quantum or classical). We can consider for definiteness a simple model of a single real scalar field $\phi$ with a potential energy density V( $\phi$ ). The total energy density is

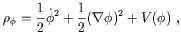
(4)

where $\nabla$ represents the spatial gradient. It is immediately clear that any solution in which the field takes on a constant value $\phi_{0}^{}$ throughout spacetime will have an energy density which is constant throughout spacetime, $\rho_{\phi}^{}$ = V( $\phi_{0}^{}$ ). The crucial point is that there is no principle or symmetry in such a theory which would prefer that V( $\phi_{0}^{}$ ) have the value zero rather than any other value. In richer theories there may be such principles, such as supersymmetry or conformal invariance; the observed world, however, shows no sign of such symmetries, so they must be severely broken if they exist at all. Hence, it requires fine-tuning to obtain a vanishing $\rho_{\rm vac}^{}$ .

We are unable to reliably calculate the expected vacuum energy in the real world, or even in some specific field theory such as the Standard Model of particle physics; at best we can offer order-of-magnitude estimates for the contributions from different sectors. In the Standard Model there are at least two important contributions, from nonvanishing condensates in the vacuum: the potential energy of the Higgs field, expected to be of the order (100 GeV)⁴ = (10¹¹ eV)⁴, and a QCD energy density in the condensate of quark bilinears $\bar{q}$ q responsible for chiral symmetry breaking, expected to be of the order (100 MeV)⁴ = (10⁸ eV)⁴. There is also a contribution from the quantum-mechanical zero-point vacuum fluctuations of each field in the model. This contribution actually diverges due to effects of very high-frequency modes; it is necessary to introduce a cutoff and hope that a more complete theory will eventually provide a physical justification for doing so. If this cutoff is at the Planck scale M_Planck = 1/ $\sqrt{8\pi G}$ = 10¹⁸ GeV, we obtain a vacuum energy of order (10¹⁸ GeV)⁴ = (10²⁷ eV)⁴. Similarly, there is no reason to exclude a "bare" classical contribution to the cosmological constant at the Planck scale, $\rho_{\Lambda_0}^{}$ ~ (10¹⁸ GeV)⁴. For any of these examples, we cannot even say with confidence whether the corresponding energy density is positive or negative; nevertheless, since there is no apparent relationship between the values of the disparate contributions, we expect the total vacuum energy to be of the same order as that of the largest components:

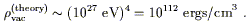
(5)

There is clearly a mismatch between the theoretical prediction (5) and the observed value (3):

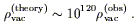
(6)

This is the famous 120-orders-of-magnitude discrepancy that makes the cosmological constant problem such a glaring embarrassment. Of course, it is somewhat unfair to emphasize the factor of 10¹²⁰, which depends on the fact that energy density has units of [energy]⁴. If we express the vacuum energy in terms of a mass scale, $\rho_{\rm vac}^{}$ = M_vac⁴, the discrepancy becomes M_vac^(theory) ~ 10³⁰M_vac^(obs); it is more accurate to think of the cosmological constant problem as a discrepancy of 30 orders of magnitude in energy scale. In fact, this problem can be ameliorated in theories where supersymmetry is spontaneously broken at a low scale, since the vacuum energy will then be given by the scale at which supersymmetry is broken (above that energy, for example, the zero-point contributions from fermions are exactly canceled by equal and opposite contributions from bosonic superpartners). If supersymmetry is preserved down to just above the weak scale, so that M_vac approx M_SUSY approx 10³ GeV, we would have M_vac^(SUSY) = 10¹⁵M_vac^(obs). In the most optimistic reading, therefore, we are left with a discrepancy of a mere fifteen orders of magnitude that we have no idea how to resolve; still, this qualifies as a problem worthy of our attention.

There have been a large number of suggested resolutions to the cosmological constant problem; see [1, 4, 6, 7, 8] for reviews. To date none has seemed exceptionally compelling, and most researchers believe that the correct solution has yet to be found.

1.3. The coincidence problem

The second issue mentioned above is the coincidence between the observed vacuum energy (3) and the current matter density. The "best-fit universe" model has $\Omega_{\Lambda 0}^{}$ = 0.7 and $\Omega_{{\rm M}0}^{}$ = 0.3, but the relative balance of vacuum and matter changes rapidly as the universe expands:

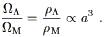
(7)

As a consequence, at early times the vacuum energy was negligible in comparison to matter and radiation, while at late times matter and radiation are negligible. There is only a brief epoch of the universe's history during which it would be possible to witness the transition from domination by one type of component to another. This is illustrated in Figure 1, in which the rate of change of $\Omega_{\Lambda}^{}$ is plotted as a function of the scale factor. At early times $\Omega_{\Lambda}^{}$ is close to zero and changing very slowly, while at late times it is close to unity and changing very slowly. It seems remarkable that we live during the short transitional period between these two eras.

Figure 1. The rate of change of the vacuum energy density parameter, d $\Omega_{\Lambda}^{}$ /da, as a function of the scale factor a, in a universe with $\Omega_{\Lambda 0}^{}$ = 0.7, $\Omega_{{\rm M}0}^{}$ = 0.3. Scale factors corresponding to the Planck era, electroweak symmetry breaking (EW), and Big Bang nucleosynthesis (BBN) are indicated, as well as the present day. The spike reflects the fact that, in such a universe, there is only a short period in which $\Omega_{\Lambda}^{}$ is evolving noticeably with time.

The approximate coincidence between matter and vacuum energies in the current universe is one of several puzzling features of the composition of the total energy density. Another great surprise is the comparable magnitudes of the baryon density ( $\Omega_{\rm b}^{}$ approx 0.04) and the density of cold non-baryonic dark matter ( $\Omega_{\rm CDM}^{}$ approx 0.25), and perhaps also that in massive neutrinos ( $\Omega_{\nu}^{}$ leq 0.01). In our current understanding, these components are relics of completely unrelated processes in the very early universe, and there seems to be no good reason why they should be of the same order of magnitude (although some specific models have been proposed). The real world seems to be a more rich and complex place than Occam's razor might have predicted. It is important to keep in mind, however, the crucial distinction between the coincidences relating the various matter components and that relating the matter and vacuum energy: the former are set once and for all by primordial processes and remain unchanged as the universe evolves, while the latter holds true only during a certain era. It is fruitless to try to explain the matter/vacuum coincidence by invoking mechanisms which make the dark energy density time-dependent in such a way as to always be proportional to that in matter; such a scenario would either imply that the dark energy would redshift away as $\rho_{\rm dark}^{}$ propto a^-3, which from (2) would lead to a non-accelerating universe, or require dramatic departures from conventional general relativity, which would in turn make it difficult to recover the successes of conventional cosmology (Big Bang nucleosynthesis, CMB anisotropy, growth of structure, and the age of the universe, to name a few). Recent observations provide some evidence that the universe has only recently entered an era of acceleration out of a previous era of deceleration [9]; although the observational case is not airtight, the conclusion seems inescapable.