2.1. An honest cosmological constant
The simplest interpretation of the dark energy is that we have
discovered that the cosmological constant is not quite zero: we
are in the lowest energy state possible (or, more properly, that
the particles we observe are excitations of such a state)
but that energy does not vanish. Although simple, this scenario
is perhaps the hardest to analyze without an understanding of
the complete cosmological constant problem, and there is
correspondingly little to say about such a possibility. As targets
to shoot for, various numerological coincidences have been
pointed out, which may some day find homes as predictions of an
actual theory. For example, the observed vacuum energy scale
Mvac = 10-3 eV
is related to the 1 TeV scale of low-energy supersymmetry breaking
models by a "supergravity suppression factor":

| (8)
|
In other words,
MSUSY is the geometric mean of
Mvac and
MPlanck. Unfortunately, nobody knows why this should be
the case. In a similar spirit, the vacuum energy density is
related to the Planck energy density by the kind of suppression
factor familiar from instanton calculations in gauge theories:

| (9)
|
In other words, the natural log of 10120 is twice 137.
Again, this is not a relation we have any right to expect to
hold (although it has been suggested that nonperturbative
effects in non-supersymmetric string theories could lead to such
an answer
[10]).
Theorists attempting to build models of a small nonzero vacuum
energy must keep in mind the requirement of remaining compatible
with some as-yet-undiscovered solution to the cosmological
constant problem. In particular, it is certainly insufficient
to describe a specific contribution to the vacuum energy which
by itself is of the right magnitude; it is necessary at the same
time for there to be some plausible reason why the well-known
and large contributions from the Standard Model could be suppressed,
while the new contribution is not.
One way to avoid this problem is to imagine that an unknown
mechanism sets the vacuum energy to zero in the state of lowest
energy, but that we actually live
in a distinct false vacuum state, almost but not quite degenerate
in energy with the true vacuum
[11,
12,
13].
From an observational point of view, false vacuum energy
and true vacuum energy are utterly indistinguishable - they both appear
as a strictly constant dark energy density. The issue with such
models is why the splitting in energies between the true and
false vacua should be so much smaller than all of the characteristic
scales of the problem; model-building approaches generally invoke
symmetries to suppress some but not all of the effects that could
split these levels.
The only theory (if one can call it that) which leads a vacuum
energy density of approximately the right order of magnitude
without suspicious fine-tuning is the anthropic principle --
the notion that intelligent observers will not witness the full
range of conditions in the universe, but only those conditions which
are compatible with the existence of such observers. Thus, we do
not consider it unnatural that human beings evolved on the surface of
the Earth rather than on that of the Sun, even though the surface
area of the Sun is much larger, since the conditions are rather
less hospitable there. If, then, there exist distinct parts of
the universe (whether they be separate spatial regions or branches
of a quantum wavefunction) in which the vacuum energy takes on
different values, we would expect to observe a value which favored the
appearance of life. Although most humans don't think of the
vacuum energy as playing any role in their lives, a substantially
larger value than we presently observe would either have led to
a rapid recollapse of the universe (if 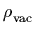 were negative)
or an inability to form galaxies (if
were negative)
or an inability to form galaxies (if 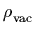 were positive).
Depending on the distribution of possible values of
were positive).
Depending on the distribution of possible values of
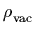 ,
one can argue that the recently observed value is in excellent
agreement with what we should expect
[14,
15,
16,
17].
Many physicists find it unappealing to think that an apparent
constant of nature would turn out to simply be a feature of our
local environment that was chosen from an ensemble of possibilities,
although we should perhaps not expect that the universe takes our
feelings into account on these matters.
More importantly, relying on the anthropic principle involves
the invocation of a large collection of alternative possibilities
for the vacuum energy, closely spaced in energy but not continuously
connected to each other (unless the light scalar
fields implied by such connected vacua is very weakly
coupled, as it must also be in the quintessence models discussed
below). It is by no means an
economical solution to the vacuum energy puzzle.
,
one can argue that the recently observed value is in excellent
agreement with what we should expect
[14,
15,
16,
17].
Many physicists find it unappealing to think that an apparent
constant of nature would turn out to simply be a feature of our
local environment that was chosen from an ensemble of possibilities,
although we should perhaps not expect that the universe takes our
feelings into account on these matters.
More importantly, relying on the anthropic principle involves
the invocation of a large collection of alternative possibilities
for the vacuum energy, closely spaced in energy but not continuously
connected to each other (unless the light scalar
fields implied by such connected vacua is very weakly
coupled, as it must also be in the quintessence models discussed
below). It is by no means an
economical solution to the vacuum energy puzzle.
As an interesting sidelight to this issue, it has been claimed that
a positive vacuum energy would be incompatible with our current
understanding of string theory
[18,
19,
20,
21].
At issue is the fact that such a universe eventually approaches a de Sitter
solution (exponentially expanding), which implies future horizons
which make it impossible to derive a gauge-invariant S-matrix.
One possible resolution might involve a dynamical
dark energy component such as
those discussed in the next section. While few string theorists
would be willing to concede that a definitive measurement that the
vacuum energy is constant with time would rule out string theory as
a description of nature, the possibility of saying something important
about fundamental theory from cosmological observations presents an
extremely exciting opportunity.
2.2. Dynamical dark energy
Although the observational evidence for dark energy implies a
component which is unclustered in space as well as slowly-varying
in time, we may still imagine that it is not perfectly
constant. The simplest possibility along these lines
involves the same kind of source
typically invoked in models of inflation in the very early universe:
a scalar field rolling slowly in a potential, sometimes known as
"quintessence"
[22,
23,
24].
There are also a number of more
exotic possibilities, including tangled topological defects and
variable-mass particles (see
[1,
7]
for references and discussion).
There are good reasons to consider dynamical dark
energy as an alternative to an honest cosmological constant.
First, a dynamical energy density can be evolving slowly to zero,
allowing for a solution to the cosmological constant problem which
makes the ultimate vacuum energy vanish exactly. Second, it poses
an interesting and challenging observational problem to study the
evolution of the dark energy, from which we might learn something
about the underlying physical mechanism. Perhaps most intriguingly,
allowing the dark energy to evolve opens the possibility
of finding a dynamical solution to the coincidence problem, if the
dynamics are such as to trigger a recent takeover by the dark energy
(independently of, or at least for a wide range of, the
parameters in the theory).
At the same time, introducing dynamics opens up the possibility
of introducing new problems, the form and severity
of which will depend on the specific
kind of model being considered. The most popular quintessence
models feature scalar fields 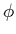 with masses of order the
current Hubble scale,
with masses of order the
current Hubble scale,

| (10)
|
(Fields with larger masses would typically have already rolled
to the minimum of their potentials.)
In quantum field theory, light scalar fields are
unnatural; renormalization effects tend to drive scalar masses
up to the scale of new physics. The well-known hierarchy
problem of particle physics amounts to asking why the Higgs
mass, thought to be of order 1011 eV, should be so much
smaller than the grand unification/Planck scale,
1025-1027 eV. Masses of 10-33 eV are
correspondingly harder to understand. At the same time, such a
low mass implies that 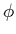 gives rise to a long-range force;
even if
gives rise to a long-range force;
even if 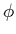 interacts with ordinary matter only through
indirect gravitational-strength couplings, searches
for fifth forces and time-dependence of coupling constants
should have already enabled us to detect the quintessence field
[25].
interacts with ordinary matter only through
indirect gravitational-strength couplings, searches
for fifth forces and time-dependence of coupling constants
should have already enabled us to detect the quintessence field
[25].
The need for delicate fine-tunings of masses and couplings in
quintessence models is certainly a strike against them, but
is not a sufficiently serious one that the idea is not worth
pursuing; until we understand much more about the dark energy,
it would be premature to rule out any idea on the basis of
simple naturalness arguments. One promising route to gaining
more understanding is to observationally characterize the time
evolution of the dark energy density. In principle any
behavior is possible, but it is sensible to choose a simple
parameterization which would characterize
dark energy evolution in the measurable regime of relatively
nearby redshifts (order unity or less). For this purpose it is
common to imagine that the dark energy evolves as a power law
with the scale factor:

| (11)
|
Even if
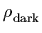 is not strictly a power law, this ansatz
can be a useful characterization of its effective behavior at
low redshifts. It is common to define an equation-of-state
parameter relating the energy density to the pressure,
is not strictly a power law, this ansatz
can be a useful characterization of its effective behavior at
low redshifts. It is common to define an equation-of-state
parameter relating the energy density to the pressure,

| (12)
|
Using the equation of energy-momentum conservation,

| (13)
|
a constant exponent n of (11) implies a constant w with

| (14)
|
As n varies from 3 (matter) to 0 (cosmological constant), w
varies from 0 to -1. (Imposing mild energy conditions implies
that | w|  1
[26];
however, models with w < - 1 are still worth considering
[27].)
1
[26];
however, models with w < - 1 are still worth considering
[27].)
Some limits from supernovae and large-scale structure from
[28]
are shown in Figure (2). These constraints
apply to the 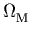 -w plane, under the assumption that the
universe is flat (
-w plane, under the assumption that the
universe is flat (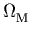 +
+ 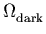 = 1). We see that
the observationally favored region features
= 1). We see that
the observationally favored region features 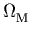
 0.35 and an honest cosmological constant, w =
- 1. However, there
is plenty of room for alternatives; one of the most important tasks
of observational cosmology will be to reduce the error regions on plots
such of these to pin down precise values of these parameters.
0.35 and an honest cosmological constant, w =
- 1. However, there
is plenty of room for alternatives; one of the most important tasks
of observational cosmology will be to reduce the error regions on plots
such of these to pin down precise values of these parameters.
To date, many investigations have considered scalar fields with
potentials that asymptote gradually to zero, of the form
e1 / 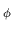 or 1/
or 1/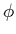 . These can have cosmologically interesting
properties, including "tracking" behavior that makes the current
energy density largely independent of the initial conditions
[29];
they can also be derived from particle-physics models, such as
the dilaton or moduli of string theory. They do not, however,
provide a solution to the coincidence problem, as the era in which
the scalar field begins to dominate is still set by finely-tuned
parameters in the theory. There have been
two scalar-field models which come closer to being solutions:
"k-essence", and oscillating dark energy. The k-essence idea
[30]
does not put the field in a shallow potential, but
rather modifies the form of the kinetic energy. We imagine that
the Lagrange density is of the form
. These can have cosmologically interesting
properties, including "tracking" behavior that makes the current
energy density largely independent of the initial conditions
[29];
they can also be derived from particle-physics models, such as
the dilaton or moduli of string theory. They do not, however,
provide a solution to the coincidence problem, as the era in which
the scalar field begins to dominate is still set by finely-tuned
parameters in the theory. There have been
two scalar-field models which come closer to being solutions:
"k-essence", and oscillating dark energy. The k-essence idea
[30]
does not put the field in a shallow potential, but
rather modifies the form of the kinetic energy. We imagine that
the Lagrange density is of the form

| (15)
|
where
X = 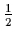 (
(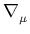
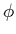 )2 is the conventional
kinetic term. For certain choices of the functions f (
)2 is the conventional
kinetic term. For certain choices of the functions f (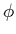 ) and
g(X), the k-essence field naturally tracks the
evolution of
the total radiation energy density during radiation domination,
but switches to being almost constant once matter begins to
dominate. In such a model the coincidence problem is explained
by the fact that matter/radiation equality was a relatively
recent occurrence (at least on a logarithmic scale). The oscillating
models
[31]
involve ordinary kinetic terms and potentials,
but the potentials take the form of a decaying exponential with
small perturbations superimposed:
) and
g(X), the k-essence field naturally tracks the
evolution of
the total radiation energy density during radiation domination,
but switches to being almost constant once matter begins to
dominate. In such a model the coincidence problem is explained
by the fact that matter/radiation equality was a relatively
recent occurrence (at least on a logarithmic scale). The oscillating
models
[31]
involve ordinary kinetic terms and potentials,
but the potentials take the form of a decaying exponential with
small perturbations superimposed:

| (16)
|
On average, the dark energy in such a model will track that of
the dominant matter/radiation component; however, there will be
gradual oscillations from a negligible density to a dominant
density and back, on a timescale set by the Hubble parameter.
Consequently, in such models the
acceleration of the universe is just something that
happens from time to time. Unfortunately, in neither
the k-essence models nor the oscillating models do we have a
compelling particle-physics motivation for the chosen dynamics,
and in both cases the behavior still depends sensitively on the
precise form of parameters and interactions chosen. Nevertheless,
these theories stand as interesting attempts to address the
coincidence problem by dynamical means.
Rather than constructing models on the basis of cosmologically
interesting dynamical properties, we may take the complementary
route of considering which models would appear most sensible from
a particle-physics point of view, and then exploring what
cosmological properties they exhibit. An acceptable particle
physics model of quintessence would be one in which the scalar
mass was naturally small and its coupling to ordinary matter
was naturally suppressed. These requirements are met by
Pseudo-Nambu-Goldstone bosons (PNGB's)
[23],
which arise in models with approximate global symmetries of the form

| (17)
|
Clearly such a symmetry should not be exact, or the potential would
be precisely flat; however, even an approximate symmetry can
naturally suppress masses and couplings. PNGB's typically
arise as the angular degrees of freedom in Mexican-hat
potentials that are "tilted" by a small explicitly symmetry
breaking, and the PNGB potential takes on a sinusoidal form:

| (18)
|
As a consequence, there is no easily characterized tracking or
attractor behavior; the equation of state parameter w will
depend on both the potential and the initial conditions, and
can take on any value from -1 to 0 (and in fact will change
with time). We therefore find that
the properties of models which are constructed by taking
particle-physics requirements as our primary concern appear
quite different from those motivated by cosmology alone. The
lesson to observational cosmologists is that a wide variety of
possible behaviors should be taken seriously, with data providing
the ultimate guidance.
2.3. Was Einstein wrong?
Given the uncomfortable tension between observational evidence for
dark energy on one hand and our intuition for what seems
natural in the context of the standard cosmological model
on the other, there is an irresistible
temptation to contemplate the possibility that we are witnessing
a breakdown of the Friedmann equation of conventional
general relativity (GR) rather than merely a novel
source of energy. Alternatives to GR are highly
constrained by tests in the solar system and in binary pulsars;
however, if we are contemplating the space of all conceivable
alternatives rather than examining one specific proposal, we are
free to imagine theories which deviate on cosmological scales while
being indistinguishable from GR in small stellar systems.
Speculations along these lines are also constrained by
observations: any alternative must predict the right abundances
of light elements from Big Bang nucleosynthesis (BBN), the correct
evolution of a sensible spectrum of primordial density fluctuations
into the observed spectrum of temperature anisotropies in the
Cosmic Microwave Background and the power spectrum of large-scale
structure, and that the age of the universe is approximately twelve
billion years. Of these phenomena, the sharpest test of
Friedmann behavior comes from BBN, since perturbation growth
depends both on the scale factor and on the local gravitational
interactions of the perturbations, while a large number of
alternative expansion histories could in principle give the same
age of the universe. As an example, Figure (3)
provides a graphical representation of alternative expansion
histories in the vicinity of BBN (
HBBN ~ 0.1 sec-1)
which predict the same light element abundances as the standard
picture [32].
The point of this figure is that expansion
histories which are not among the family portrayed, due to
differences either in the slope or the overall normalization,
will not give the right abundances. So it is possible to find
interesting nonstandard cosmologies which are consistent with
the data, but they describe a small set in the
space of all such alternatives.
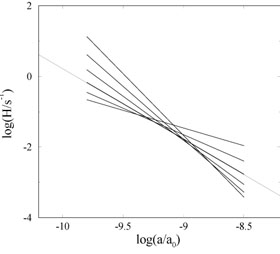
|
Figure 3. The range of allowed evolution
histories during Big Bang
nucleosynthesis (between temperatures of 1 MeV to 50 keV),
expressed as the behavior of the Hubble parameter
H = 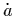 /a as a function of a. Changes in the
normalization
of H can be compensated by a change in the slope while
predicting the same abundances of 4He, 2D, and
7Li.
The extended thin line represents the standard radiation-dominated
Friedmann universe model. From
[32]. /a as a function of a. Changes in the
normalization
of H can be compensated by a change in the slope while
predicting the same abundances of 4He, 2D, and
7Li.
The extended thin line represents the standard radiation-dominated
Friedmann universe model. From
[32].
|
Rather than imagining that gravity follows the predictions of
standard GR in localized systems but deviates in cosmology, another
approach would be to imagine that GR breaks down whenever the
gravitational field becomes (in some sense) sufficiently weak.
This would be unusual behavior, as we are used to thinking of
effective field theories as breaking down at high energies and
small length scales, but being completely reliable in the
opposite regime. On the other hand, we might be ambitious enough to
hope that an alternative theory of gravity could explain away
not only the need for dark energy but also that for dark matter.
It has been famously pointed out by Milgrom
[33]
that the observed dynamics of galaxies only requires the
introduction of dark matter in regimes where the acceleration
due to gravity (in the Newtonian sense) falls below a certain
fixed value,

| (19)
|
Meanwhile, we seem to need to invoke dark energy when the Hubble
parameter drops approximately to its current value,

| (20)
|
A priori, there seems to be little reason to expect that
these two phenomena should be characterized by timescales of
the same order of magnitude; one involves the local dynamics of
baryons and non-baryonic dark matter, while the other involves
dark energy and the overall matter density (although see
[34]
for a suggested explanation).
It is natural to wonder whether this is simply a numerical
coincidence, or the reflection of some new underlying theory
characterized by a single dimensionful parameter. To date,
nobody has succeeded in inventing a theory which comes anything
close to explaining away both the dark matter and dark energy
in terms of modified gravitational dynamics. Given the
manifold successes of the dark matter paradigm, from gravitational
lensing to structure formation to CMB anisotropy, is seems a good
bet to think that this numerical coincidence is simply an
accident. Of course, given the incredible importance of finding
a successful alternative theory, there seems to be little harm in
keeping an open mind.
It was mentioned above, and bears repeating, that modified-gravity
models do not hold any unique promise for solving the
coincidence problem. At first glance we might hope that an
alternative to the conventional Friedmann equation might lead to
a naturally occurring acceleration at all times; but a moment's
reflection reveals that perpetual acceleration is not consistent
with the data, so we still require an explanation for why the
acceleration began recently. In other words, the observations
seem to be indicating the importance of a fixed scale at which
the universe departs from ordinary matter domination; if we
are fortunate we will explain this scale either in terms of
combinations of other scales in our particle-physics model or
as an outcome of dynamical processes, while if we are
unfortunate it will have to be a new input parameter to our
theory. In either case, finding the origin of this new scale is
the task for theorists and experimenters in the near future.








![]() were negative)
or an inability to form galaxies (if
were negative)
or an inability to form galaxies (if ![]() were positive).
Depending on the distribution of possible values of
were positive).
Depending on the distribution of possible values of
![]() ,
one can argue that the recently observed value is in excellent
agreement with what we should expect
[14,
15,
16,
17].
Many physicists find it unappealing to think that an apparent
constant of nature would turn out to simply be a feature of our
local environment that was chosen from an ensemble of possibilities,
although we should perhaps not expect that the universe takes our
feelings into account on these matters.
More importantly, relying on the anthropic principle involves
the invocation of a large collection of alternative possibilities
for the vacuum energy, closely spaced in energy but not continuously
connected to each other (unless the light scalar
fields implied by such connected vacua is very weakly
coupled, as it must also be in the quintessence models discussed
below). It is by no means an
economical solution to the vacuum energy puzzle.
,
one can argue that the recently observed value is in excellent
agreement with what we should expect
[14,
15,
16,
17].
Many physicists find it unappealing to think that an apparent
constant of nature would turn out to simply be a feature of our
local environment that was chosen from an ensemble of possibilities,
although we should perhaps not expect that the universe takes our
feelings into account on these matters.
More importantly, relying on the anthropic principle involves
the invocation of a large collection of alternative possibilities
for the vacuum energy, closely spaced in energy but not continuously
connected to each other (unless the light scalar
fields implied by such connected vacua is very weakly
coupled, as it must also be in the quintessence models discussed
below). It is by no means an
economical solution to the vacuum energy puzzle.
![]() with masses of order the
current Hubble scale,
with masses of order the
current Hubble scale,

![]() gives rise to a long-range force;
even if
gives rise to a long-range force;
even if ![]() interacts with ordinary matter only through
indirect gravitational-strength couplings, searches
for fifth forces and time-dependence of coupling constants
should have already enabled us to detect the quintessence field
[25].
interacts with ordinary matter only through
indirect gravitational-strength couplings, searches
for fifth forces and time-dependence of coupling constants
should have already enabled us to detect the quintessence field
[25].

![]() is not strictly a power law, this ansatz
can be a useful characterization of its effective behavior at
low redshifts. It is common to define an equation-of-state
parameter relating the energy density to the pressure,
is not strictly a power law, this ansatz
can be a useful characterization of its effective behavior at
low redshifts. It is common to define an equation-of-state
parameter relating the energy density to the pressure,



 1
[26];
however, models with w < - 1 are still worth considering
[27].)
1
[26];
however, models with w < - 1 are still worth considering
[27].)
![]() -w plane, under the assumption that the
universe is flat (
-w plane, under the assumption that the
universe is flat (![]() +
+ ![]() = 1). We see that
the observationally favored region features
= 1). We see that
the observationally favored region features ![]()
![]() 0.35 and an honest cosmological constant, w =
- 1. However, there
is plenty of room for alternatives; one of the most important tasks
of observational cosmology will be to reduce the error regions on plots
such of these to pin down precise values of these parameters.
0.35 and an honest cosmological constant, w =
- 1. However, there
is plenty of room for alternatives; one of the most important tasks
of observational cosmology will be to reduce the error regions on plots
such of these to pin down precise values of these parameters.
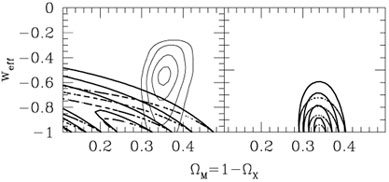
![]() +
+ ![]() = 1. The left-hand panel
shows limits from supernova data (lower left corner) and large-scale
structure (ellipses); the right-hand panel shows combined
constraints. From
[28].
= 1. The left-hand panel
shows limits from supernova data (lower left corner) and large-scale
structure (ellipses); the right-hand panel shows combined
constraints. From
[28].
![]() or 1/
or 1/![]() . These can have cosmologically interesting
properties, including "tracking" behavior that makes the current
energy density largely independent of the initial conditions
[29];
they can also be derived from particle-physics models, such as
the dilaton or moduli of string theory. They do not, however,
provide a solution to the coincidence problem, as the era in which
the scalar field begins to dominate is still set by finely-tuned
parameters in the theory. There have been
two scalar-field models which come closer to being solutions:
"k-essence", and oscillating dark energy. The k-essence idea
[30]
does not put the field in a shallow potential, but
rather modifies the form of the kinetic energy. We imagine that
the Lagrange density is of the form
. These can have cosmologically interesting
properties, including "tracking" behavior that makes the current
energy density largely independent of the initial conditions
[29];
they can also be derived from particle-physics models, such as
the dilaton or moduli of string theory. They do not, however,
provide a solution to the coincidence problem, as the era in which
the scalar field begins to dominate is still set by finely-tuned
parameters in the theory. There have been
two scalar-field models which come closer to being solutions:
"k-essence", and oscillating dark energy. The k-essence idea
[30]
does not put the field in a shallow potential, but
rather modifies the form of the kinetic energy. We imagine that
the Lagrange density is of the form

![]() (
(![]()
![]() )2 is the conventional
kinetic term. For certain choices of the functions f (
)2 is the conventional
kinetic term. For certain choices of the functions f (![]() ) and
g(X), the k-essence field naturally tracks the
evolution of
the total radiation energy density during radiation domination,
but switches to being almost constant once matter begins to
dominate. In such a model the coincidence problem is explained
by the fact that matter/radiation equality was a relatively
recent occurrence (at least on a logarithmic scale). The oscillating
models
[31]
involve ordinary kinetic terms and potentials,
but the potentials take the form of a decaying exponential with
small perturbations superimposed:
) and
g(X), the k-essence field naturally tracks the
evolution of
the total radiation energy density during radiation domination,
but switches to being almost constant once matter begins to
dominate. In such a model the coincidence problem is explained
by the fact that matter/radiation equality was a relatively
recent occurrence (at least on a logarithmic scale). The oscillating
models
[31]
involve ordinary kinetic terms and potentials,
but the potentials take the form of a decaying exponential with
small perturbations superimposed:




![]() /a as a function of a. Changes in the
normalization
of H can be compensated by a change in the slope while
predicting the same abundances of 4He, 2D, and
7Li.
The extended thin line represents the standard radiation-dominated
Friedmann universe model. From
[32].
/a as a function of a. Changes in the
normalization
of H can be compensated by a change in the slope while
predicting the same abundances of 4He, 2D, and
7Li.
The extended thin line represents the standard radiation-dominated
Friedmann universe model. From
[32].

