


The biggest stumbling-block for attempts to confront theories of cosmological structure formation with observations of galaxy clustering is the uncertain and possibly biased relationship between galaxies and the distribution of gravitating matter. The idea that galaxy formation might be biased goes back to the realization by Kaiser (1984) that the reason Abell clusters display stronger correlations than galaxies at a given separation is that these objects are selected to be particularly dense concentrations of matter. As such, they are very rare events, occurring in the tail of the distribution function of density fluctuations. Under such conditions a ``high-peak'' bias prevails: rare high peaks are much more strongly clustered than more typical fluctuations (Bardeen et al. 1986). If the properties of a galaxy (its morphology, color, luminosity) are influenced by the density of its parent halo, for example, then differently-selected galaxies are expected to a different bias (e.g. Dekel & Rees 1987). Observations show that different kinds of galaxy do cluster in different ways (e.g. Loveday et al. 1995; Hermit et al. 1996).
In local bias models, the propensity of a galaxy to form at
a point where the total (local) density of matter is
 is
taken to be some function f
(
is
taken to be some function f
( )
(Coles 1993,
hereafter C93;
Fry & Gaztanaga
1993,
hereafter FG93). It is possible to place
stringent constraints on the effect this kind of bias can have on
galaxy clustering statistics without making any particular
assumption about the form of f. In this Letter, we
describe the results of a different approach to local bias models
that exploits new results from the theory of hierarchical
clustering in order to place stronger constraints on what a local
bias can do to galaxy clustering. We leave the technical details to
Munshi et al. (1999a,
b) and
Bernardeau &
Schaeffer (1999);
here we shall simply motivate and present the results and explain
their importance in a wider context.
)
(Coles 1993,
hereafter C93;
Fry & Gaztanaga
1993,
hereafter FG93). It is possible to place
stringent constraints on the effect this kind of bias can have on
galaxy clustering statistics without making any particular
assumption about the form of f. In this Letter, we
describe the results of a different approach to local bias models
that exploits new results from the theory of hierarchical
clustering in order to place stronger constraints on what a local
bias can do to galaxy clustering. We leave the technical details to
Munshi et al. (1999a,
b) and
Bernardeau &
Schaeffer (1999);
here we shall simply motivate and present the results and explain
their importance in a wider context.
The fact that Newtonian
gravity is scale-free suggests that the N-point correlation
functions of self-gravitating particles,
 N,
evolved into the
large-fluctuation regime by the action of gravity, should obey a
scaling relation of the form
N,
evolved into the
large-fluctuation regime by the action of gravity, should obey a
scaling relation of the form
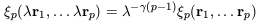
| (39) |
when the elements of a structure are scaled by a factor
 (e.g. Balian & Schaeffer 1989).
Observations offer some support
for such an idea, in that the observed two-point correlation
function
(e.g. Balian & Schaeffer 1989).
Observations offer some support
for such an idea, in that the observed two-point correlation
function  (r)
of galaxies is reasonably well represented by a
power law over a large range of length scales,
(r)
of galaxies is reasonably well represented by a
power law over a large range of length scales,
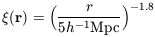
| (40) |
(Groth & Peebles
1977;
Davis & Peebles
1977)
for r between, say, 100h-1 kpc and
10h-1 Mpc. The observed three point function,
 3,
is well-established to have a hierarchical form
3,
is well-established to have a hierarchical form
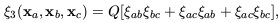
| (41) |
where
 ab =
ab =
 (xa,
xb), etc, and Q is a constant
(Davis & Peebles
1977;
Groth & Peebles
1977).
The four-point
correlation function can be expressed as a combination of graphs
with two different topologies - ``snake'' and ``star'' - with
corresponding (constant) amplitudes Ra and
Rb respectively:
(xa,
xb), etc, and Q is a constant
(Davis & Peebles
1977;
Groth & Peebles
1977).
The four-point
correlation function can be expressed as a combination of graphs
with two different topologies - ``snake'' and ``star'' - with
corresponding (constant) amplitudes Ra and
Rb respectively:
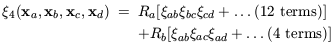
| (42) |
(e.g. Fry & Peebles 1978; Fry 1984).
It is natural to guess that all p-point correlation functions can
be expressed as a sum over all possible p-tree graphs with (in
general) different amplitudes
Qp,  for
each tree diagram topology
for
each tree diagram topology  .
If it is further assumed that there is
no dependence of these amplitudes upon the shape of the diagram,
rather than its topology, the correlation functions should obey
the following relation:
.
If it is further assumed that there is
no dependence of these amplitudes upon the shape of the diagram,
rather than its topology, the correlation functions should obey
the following relation:
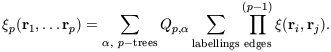
| (43) |
To go further it is necessary to find a way of
calculating Qp. One possibility, which appears remarkably
successful when compared with numerical experiments
(Munshi et al. 1999b;
Bernardeau &
Schaeffer 1999),
is to calculate the
amplitude for a given graph by simply assigning a weight to each
vertex of the diagram  n,
where n is the order of the
vertex (the number of lines that come out of it), regardless of
the topology of the diagram in which it occurs. In this case
n,
where n is the order of the
vertex (the number of lines that come out of it), regardless of
the topology of the diagram in which it occurs. In this case
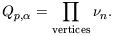
| (44) |
Averages of higher-order correlation functions can be defined as
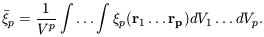
| (45) |
Higher-order statistical properties of galaxy counts
are often described in terms of the scaling parameters Sp
constructed from the
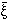 p
via
p
via
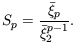
| (46) |
It is a consequence of the particular class of hierarchical clustering models defined by equations (5) & (6) that all the Sp should be constant, independent of scale.
Using a generating function technique
[Bernardeau &
Schaeffer 1992]
it is possible
to derive a series expansion for the m-point count probability
distribution function of the objects
Pm(N1, .... Nm)
(the joint
probability of finding Ni objects in the i-th
cell, where i runs from 1 to m) from the
 n. The hierarchical model
outlined above is therefore statistically complete. In principle,
therefore, any statistical property of the evolved distribution of
matter can be calculated just as it can for a Gaussian random
field. This allows us to extend various results concerning the
effects of biasing on the initial conditions into the nonlinear
regime in a more elegant way than is possible using other
approaches to hierarchical clustering.
n. The hierarchical model
outlined above is therefore statistically complete. In principle,
therefore, any statistical property of the evolved distribution of
matter can be calculated just as it can for a Gaussian random
field. This allows us to extend various results concerning the
effects of biasing on the initial conditions into the nonlinear
regime in a more elegant way than is possible using other
approaches to hierarchical clustering.
For example, let us consider the joint probability P2(N1, N2) for two cells to contain N1 and N2 particles respectively. Using the generating-function approach outlined above, it is quite easy to show that, at lowest order,
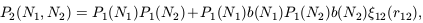
| (47) |
where the P1(Ni) are the
individual count probabilities of each volume separately and
 12 is the
underlying mass correlation function. The
function b(Ni) we have introduced in (9)
depends on the set of
12 is the
underlying mass correlation function. The
function b(Ni) we have introduced in (9)
depends on the set of
 n appearing in equation
(6); its precise form does not
matter in this context, but the structure of equation (9) is very
useful. We can use (9) to define
n appearing in equation
(6); its precise form does not
matter in this context, but the structure of equation (9) is very
useful. We can use (9) to define
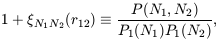
| (48) |
where  N1N2(r12)
is the cross-correlation of
``cells'' of occupancy N1 and N2
respectively. From this
definition and equation (9) it follows that
N1N2(r12)
is the cross-correlation of
``cells'' of occupancy N1 and N2
respectively. From this
definition and equation (9) it follows that
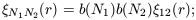
| (49) |
we have dropped the subscripts on r for clarity from now on. From (11) we can obtain
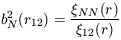
| (50) |
for the special case where N1 = N2 =
N which can be identified
with the usual definition of the bias parameter associated with
the correlations among a given set of objects
 obj(r)
= b2obj
obj(r)
= b2obj
 mass(r).
Moreover, note that at
this order (which is valid on large scales), the correlation bias
defined by equation (11) factorizes into contributions
bNi
from each individual cell
(Bernardeau 1996;
Munshi et al. 1999b).
mass(r).
Moreover, note that at
this order (which is valid on large scales), the correlation bias
defined by equation (11) factorizes into contributions
bNi
from each individual cell
(Bernardeau 1996;
Munshi et al. 1999b).
Coles (1993)
proved, under weak conditions on the form of a local
bias f ( )
as discussed in the introduction, that the
large-scale biased correlation function would generally have a
leading order term proportional to
)
as discussed in the introduction, that the
large-scale biased correlation function would generally have a
leading order term proportional to  12(r12).
In other words, one cannot change the large-scale slope of the correlation
function of locally-biased galaxies with respect to that of the
mass. This ``theorem'' was proved for bias applied to Gaussian
fluctuations only and therefore does not obviously apply to galaxy
clustering, since even on large scales deviations from Gaussian
behaviour are significant. It also has a more minor loophole,
which is that for certain peculiar forms of f the leading order
term is proportional to
12(r12).
In other words, one cannot change the large-scale slope of the correlation
function of locally-biased galaxies with respect to that of the
mass. This ``theorem'' was proved for bias applied to Gaussian
fluctuations only and therefore does not obviously apply to galaxy
clustering, since even on large scales deviations from Gaussian
behaviour are significant. It also has a more minor loophole,
which is that for certain peculiar forms of f the leading order
term is proportional to
 122,
which falls off more sharply
than
122,
which falls off more sharply
than  12
on large scales.
12
on large scales.
Steps towards the plugging of this gap began with FG93 who used an
expansion of f in powers of
 and weakly non-linear
(perturbative) calculations of
and weakly non-linear
(perturbative) calculations of
 12(r)
to explore the
statistical consequences of biasing in more realistic (i.e.
non-Gaussian) fields. Based largely on these arguments,
Scherrer &
Weinberg (1998),
hereafter SW98, confirmed the validity of the
C93 result in the non-linear regime, and also showed explicitly
that non-linear evolution always guarantees the existence of a
linear leading-order term regardless of f, thus plugging the
small gap in the original C93 argument. These works have a similar
motivation the approach I am discussing here, and also exploit
hierarchical scaling arguments of the type discussed above en
route to their conclusions. What is different about the approach
we have used in this paper is that the somewhat cumbersome
simultaneous expansion of f and
12(r)
to explore the
statistical consequences of biasing in more realistic (i.e.
non-Gaussian) fields. Based largely on these arguments,
Scherrer &
Weinberg (1998),
hereafter SW98, confirmed the validity of the
C93 result in the non-linear regime, and also showed explicitly
that non-linear evolution always guarantees the existence of a
linear leading-order term regardless of f, thus plugging the
small gap in the original C93 argument. These works have a similar
motivation the approach I am discussing here, and also exploit
hierarchical scaling arguments of the type discussed above en
route to their conclusions. What is different about the approach
we have used in this paper is that the somewhat cumbersome
simultaneous expansion of f and
 12 used
by SW98 is not
required in this calculation. The generating functions to proceed
directly to the joint probability (9), while SW98 have to perform
a complicated sum over moments of a bivariate distribution. The
factorization of the probability distribution (9) is also a
stronger result than that presented by SW98, in that it leads
almost trivially to the C93 ``theorem'' but also generalizes to
higher-order correlations than the two-point case under discussion here.
12 used
by SW98 is not
required in this calculation. The generating functions to proceed
directly to the joint probability (9), while SW98 have to perform
a complicated sum over moments of a bivariate distribution. The
factorization of the probability distribution (9) is also a
stronger result than that presented by SW98, in that it leads
almost trivially to the C93 ``theorem'' but also generalizes to
higher-order correlations than the two-point case under discussion here.
Note that the density of a cell of given volume is simply
proportional to its occupation number N. The factorizability of
the dependence of
 N1N2(r12)
upon b(N1) and
b(N2) in (11) means that applying a local bias
f (
N1N2(r12)
upon b(N1) and
b(N2) in (11) means that applying a local bias
f ( ) boils
down to applying some bias function
F(N) = f[b(N)] to each cell.
Integrating over all N thus leads directly to the same
conclusion as C93, i.e. that the large-scale
) boils
down to applying some bias function
F(N) = f[b(N)] to each cell.
Integrating over all N thus leads directly to the same
conclusion as C93, i.e. that the large-scale
 (r) of
locally-biased objects is proportional to the underlying matter
correlation function. This has also been confirmed by numerically
using N-body experiments
(Mann et al. 1998;
Narayanan et al. 1998).
(r) of
locally-biased objects is proportional to the underlying matter
correlation function. This has also been confirmed by numerically
using N-body experiments
(Mann et al. 1998;
Narayanan et al. 1998).
In hierarchical models, galaxy formation involves the following three stages:
Rather than attempting to model these stages in one go by a simple function f of the underlying density field it is interesting to see how each of these selections might influence the resulting statistical properties. Bardeen et al. (1986), inspired by Kaiser (1984), pioneered this approach by calculating detailed statistical properties of high-density regions in Gaussian fluctuations fields. Mo & White (1996) and Mo et al. (1997) went further along this road by using an extension of the Press-Schechter (1974) theory to calculate the correlation bias of halos, thus making an attempt to correct for the dynamical evolution absent in the Bardeen et al. approach. The extended Press-Schechter approach seem to be in good agreement with numerical simulations, except for small halo masses (Jing 1998). It forms the basis of many models for halo bias in the subsequent literature (e.g. Moscardini et al. 1998; Tegmark & Peebles 1998).
The hierarchical models furnish an elegant extension of this work that incorporates both density-selection and non-linear dynamics in an alternative to the Mo & White (1996) approach. We exploit the properties of equation (47) to construct the correlation function of volumes where the occupation number exceeds some critical value. For very high occupations these volumes should be in good correspondence with collapsed objects.
The way of proceeding is to construct a tree graph for all the
points in both volumes. One then has to re-partition the elements
of this graph into internal lines (representing the correlations
within each cell) and external lines (representing inter-cell
correlations). Using this approach the distribution of
high-density regions in a field whose correlations are given by
eq. (5) can be shown to be itself described by a hierarchical
model, but one in which the vertex weights, say Mn, are
different from the underlying weights
 n
(Bernardeau &
Schaeffer 1992,
1999;
Munshi et al. 1999a,
b).
n
(Bernardeau &
Schaeffer 1992,
1999;
Munshi et al. 1999a,
b).
First note that a density threshold is in fact a form of local bias, so the effects of halo bias are governed by the same strictures as described in the previous section. Many of the other statistical properties of the distribution of dense regions can be reduced to a dependence on a scaling parameter x, where
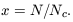
| (51) |
In this definition
Nc = 
 2,
where
2,
where 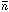 is the mean number of
objects in the cell and
is the mean number of
objects in the cell and
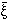 2 is
defined by eq.
(45) with p = 2. The scaling parameters Sp can be
calculated as functions of x, but are generally rather messy
(Munshi et al. 1999a).
The most interesting limit when x >> 1
is, however, rather simple. This is because the vertex weights
describing the distribution of halos depend only on the
2 is
defined by eq.
(45) with p = 2. The scaling parameters Sp can be
calculated as functions of x, but are generally rather messy
(Munshi et al. 1999a).
The most interesting limit when x >> 1
is, however, rather simple. This is because the vertex weights
describing the distribution of halos depend only on the
 n
and this dependence cancels in the ratio (46). In this regime,
n
and this dependence cancels in the ratio (46). In this regime,
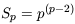
| (52) |
for all possible hierarchical models. The reader is referred to Munshi et al. (1999a) for details. This result is also obtained in the corresponding limit for very massive halos by Mo et al. (1997). The agreement between these two very different calculations supports the inference that this is a robust prediction for the bias inherent in dense regions of a distribution of objects undergoing gravity-driven hierarchical clustering.
The main purpose of this lecture has been to discuss recent developments in the theory of gravitational-driven hierarchical clustering. The model described in equations (5) & (6) provides a statistically-complete prescription for a density field that has undergone hierarchical clustering. This allows us to improve considerably upon biasing arguments based on an underlying Gaussian field.
These methods allow a simpler proof of the result obtained by SW98 that strong non-linear evolution does not invalidate the local bias theorem of C93. They also imply that the effect of bias on a hierarchical density field is factorizable. A special case of this is the bias induced by selecting regions above a density threshold. The separability of bias predicted in this kind of model could be put to the test if a population of objects could be found whose observed characteristics (luminosity, morphology, etc.) were known to be in one-to-one correspondence with the halo mass. Likewise, the generic prediction of higher-order correlation behaviour described by the behaviour of Sp in equation (46) can also be used to construct a test of this particular form of bias.
Referring to the three stages of galaxy formation described in §
4, analytic theory has now developed to the point where it is
fairly convincing on (1) the formation of halos. Numerical
experiments are beginning now to handle (2) the behaviour of the gas component
(Blanton et al. 1998,
1999).
But it is unlikely that
much will be learned about (3) by theoretical arguments in the
near future as the physics involved is poorly understood (though
see Benson et
al. 1999).
Arguments have already been advanced to
suggest that bias might not be a deterministic function of
 ,
perhaps because of stochastic or other hidden effects
(Dekel & Lahav
1998;
Tegmark &
Bromley 1999).
It also remains possible
that large-scale non-local bias might be induced by environmental effects
(Babul & White
1991;
Bower et al. 1993).
,
perhaps because of stochastic or other hidden effects
(Dekel & Lahav
1998;
Tegmark &
Bromley 1999).
It also remains possible
that large-scale non-local bias might be induced by environmental effects
(Babul & White
1991;
Bower et al. 1993).
Before adopting these more complex models, however, it is important to exclude the simplest ones, or at least deal with that part of the bias that is attributable to known physics. At this stage this means that the `minimal' bias model should be that based on the selection of dark matter halos. Establishing the extent to which observed galaxy biases can be explained in this minimal way is clearly an important task.