Hubble (1936) divided the "regular nebulae" into two classes, the spirals and the ellipticals, defining the latter as "highly concentrated and [showing] no indications of resolution into stars." He emphasized the featureless appearance of most "elliptical nebulae" and noted that only two of their characteristics were useful for further classification: the shapes of their isophotal contours; and their luminosity gradients. The latter were difficult to measure quantitatively at the time, and Hubble based his classification scheme entirely on the ellipticity (a - b)/a, with a and b the major and minor axis lengths. Hubble understood that the observed ellipticity was only a lower limit to the true elongation due to the unknown orientation of a galaxy's "polar axis;" he called this uncertainty "serious, but unavoidable." Nevertheless he was able to compute an estimate of the frequency function of intrinsic shapes by assuming that elliptical galaxies were oblate spheroids with random orientations ([Hubble 1926]).
Hubble's remarks remain nearly as valid today as they were six decades ago. Classification of elliptical galaxies is still based almost entirely on their luminosity distributions; and although Hubble's analysis of the intrinsic shape distribution has been considerably refined, we still know little of a definite nature about the three-dimensional shapes of these systems. An important shift in our understanding of elliptical galaxies took place in 1975, following the discovery that most ellipticals rotate significantly more slowly than expected for a fluid body with the same flattening ([Bertola & Capaccioli 1975]). Elliptical galaxies were revealed to be "hot" stellar systems, in which most of the support against gravitational collapse comes from essentially random motions rather than from ordered rotation. Two questions immediately arose from these observations: what produces the observed flattenings; and, given that rotation plays only a minor role, are elliptical galaxies axisymmetric or fully triaxial? Binney (1978) suggested that the flattenings were due in large part to anisotropic velocity distributions and noted that triaxial figures were no less likely than axisymmetric ones. His suggestion was quickly followed up by Schwarzschild (1979, 1982) who showed that self-consistent triaxial models could be constructed by superposition of time-averaged orbits. The phenomenon of triaxiality has since remained central to our understanding of elliptical galaxy dynamics.
Following Schwarzschild's pioneering work, a common theme of dynamical studies has been the essentially regular character of the motion in triaxial potentials, a point of view reflected also in many review articles ([Binney 1982c]; [de Zeeuw & Franx 1991]; [Gerhard 1994]; [de Zeeuw 1996]) and texts ([Fridman & Polyachenko 1984]; [Saslaw 1985]; [Binney & Tremaine 1987]). Regular motion - that is, motion that respects as many integrals as there are degrees of freedom - is crucial for the success of the self-consistency studies, since regular orbits have a variety of time-averaged shapes that make them well suited to reproducing the mass distribution of an elongated or triaxial galaxy ([Schwarzschild 1981]). However this view was challenged by the discovery, around 1993, that the luminosity profiles of real elliptical galaxies continue to rise, roughly as power laws, into the smallest observable radii ([Crane et al. 1993]; [Ferrarese et al. 1994]). There is also growing evidence that most elliptical galaxies and bulges contain supermassive black holes at their centers, presumably relics of the quasar epoch ([Kormendy & Richstone 1995]). The orbital motion in triaxial models with central cusps or black holes can be very different from the motion in models like Schwarzschild's, which had a large, constant-density core. Many orbits - particulary the box-like orbits that visit the center - are found to be chaotic, densely filling a region that is much rounder than an isodensity contour. The non-integrability of realistic triaxial potentials is reflected also in the character of the regular orbits, which are strongly influenced by resonances between the frequencies of motion in different directions. A growing body of work supports the view that the dynamical influence of central density cusps and black holes can extend far beyond the nucleus of a triaxial galaxy, and may be responsible for many of the large-scale systematic properties of elliptical galaxies, including the fact that few of these systems exhibit strong evidence for triaxiality.
Non-integrability and its consequences are therefore the major themes of the present review. A number of other topics are highlighted here, both because of their intrinsic importance and because of their relative neglect in recent reviews. These topics include torus construction; dynamical instabilities; and mechanisms for collisionless relaxation. Among the important topics not treated in detail here are intrinsic shapes (recently reviewed by Statler 1995); galaxy interactions and mergers ([Barnes 1996]); and dynamical studies of the distribution of dark matter ([Bridges 1999]; [Sackett 1999]).
A number of standard formulae are in use for describing the density and potential of three-dimensional galaxies. Several of the most common are defined here and referred to below. Some of these formulae were intended to mimic the luminosity profiles of real galaxies; others are poor descriptions of real galaxies but have features that make them useful from a computational point of view. Models, like Hénon's isochrone, that were first defined in the spherical geometry are often generalized to the ellipsoidal case by replacing the radial variable r with m, where m2 = (x / a)2 + (y / b)2 + (z / c)2 is constant on ellipsoidal shells.
1. The logarithmic potential:
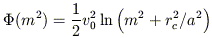
| (1) |
whose large-radius dependence corresponds to a density that falls off as r-2. The isodensity contours are peanut-shaped and the density falls below zero on the short axis when the elongation is sufficiently great.
2. The Perfect Ellipsoid:
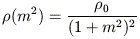
| (2) |
([Kuzmin 1956], 1973; [de Zeeuw 1985b]). The Perfect Ellipsoid is the most general, ellipsoidally-stratified mass model whose gravitational potential supports three isolating integrals of the motion.
3. The "imperfect ellipsoid":
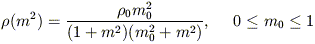
| (3) |
where
0 =
M(1 + m0) /
(2
2
abcm02)
([Merritt &
Valluri 1996]).
For m0 = 1, the Perfect density law is recovered,
while for m0 = 0 the density increases as
r-2 near the center.
The potential and forces can be efficiently calculated after a
transformation to ellipsoidal coordinates.
4. Hénon's isochrone, a spherical model with the potential:
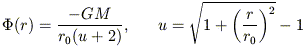
| (4) |
([Hénon 1959a], b). The name "isochrone" refers to the independence of the radial frequency of an orbit on its angular momentum. The action-angle variables corresponding to quasiperiodic motion in the isochrone potential can be expressed in terms of simple functions (e.g. [Gerhard & Saha 1991]).
5. Dehnen's law:
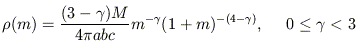
| (5) |
with M the total mass ([Dehnen 1993]). The potential in the triaxial geometry may be expressed in terms of one-dimensional integrals ([Merritt & Fridman 1996]). Dehnen's law has a power-law central density dependence which approximates the observed luminosity profiles of early-type galaxies. Its large-radius dependence is steeper than that of real elliptical galaxies.