5. ORIGIN OF THE M - RELATION

The greatest dividend to come so far from the M - relation has been the resolution of the apparent discrepancy between black hole masses in nearby galaxies, the masses of black holes in AGN, and the mass density in black holes needed to explain quasar light. But the importance of the M - relation presumably goes beyond its ability to clarify the data. Like other tight, empirical correlations in astronomy, the M - relation must be telling us something fundamental about origins, and in particular, about the connection between black hole mass and bulge properties.

Probably the simplest way to relate black holes to bulges is to assume a fixed ratio of M to M_bulge. Since M (Eq. 2), this assumption implies M_bulge . In fact this is well known to be the case: bulge luminosities scale as ~ ⁴, the Faber-Jackson law, and mass-to-light ratios scale as ~ L^1/4 (Faber et al. 1987), giving M_bulge ~ ⁵, in agreement with the slope = 4.5±0.5 derived above for the M - relation.

On the other hand, the M - relation appears to be much tighter than the relation between and bulge mass or luminosity. And even if a tight correlation between black hole mass and bulge mass were set up in the early universe, it is hard to see how it could survive mergers, which readily convert disks to bulges and may also channel gas into the nucleus, producing (presumably) uncorrelated changes in M and M_bulge. The tightness of the M - relation suggests that some additional feedback mechanism acts to more directly connect black hole masses to stellar velocity dispersions and to maintain that connection in spite of mergers.

One such feedback mechanism was suggested by Silk & Rees (1998) even before the discovery of the M - relation. These authors explored a model in which supermassive black holes first form via collapse of ~ 10⁶ M gas clouds before most of the bulge mass has turned into stars. The black holes created in this way would then accrete and radiate, driving a wind which acts back on the accretion flow. Ignoring star formation, departures from spherical symmetry etc., the flow would stall if the rate of deposition of mechanical energy into the infalling gas was large enough to unbind the protogalaxy in a crossing time T_D. Taking for the energy deposition rate some fraction f of the Eddington luminosity L_E, we have

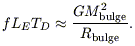
(3)

Writing GM_bulge ² R_bulge, T_D R_bulge / and L_E = 4 cGM / with the opacity,

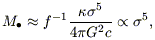
(4)

consistent with the observed relation. The constant of proportionality works out to be roughly correct if f ~ 0.01 - 0.1 (Silk & Rees 1998).

This model assumes that black holes acquire most of their mass during a fast accretion phase, t_acc 10⁷ yr. Kauffmann & Haehnelt (2000) developed a semi-analytic model for galaxy formation in which black holes grow progressively larger during galaxy mergers. The cooling of the gas that falls in during mergers is assumed to be partially balanced by energy input from supernovae. This feedback is stronger for smaller galaxies which has the effect of steepening the resulting relation between M and . Haehnelt & Kauffmann (2000) found M ~ ^3.5 but the slope could easily have been increased if the feedback had been set higher (M. Haehnelt, private communication). However the scatter in the M - relation derived by them was only slightly less than the scatter in M vs L_bulge, in apparent contradiction with the observations (Figure 1).

Burkert & Silk (2001) also considered a model in which black holes grow by accreting gas during mergers. In their model, accretion is halted when star formation begins to exhaust the gas in the outer accreting disk; the viscous accretion rate is proportional to, and assuming a star formation time scale that is proportional to T_D, Burkert & Silk found M R_bulge ²/G M_bulge, with a constant of proportionality that is again similar to that observed. This model does not give a convincing explanation for the tight correlation of M with however.

Feedback of a very different sort was proposed by Norman, Sellwood & Hasan (1996), Merritt & Quinlan (1998) and Sellwood & Moore (1999). These authors simulated the growth of massive compact objects at the centers of barred or triaxial systems and noted how the nonaxisymmetric component was weakened or dissolved when the central mass exceeded a few percent of the stellar mass. Since departures from axisymmetry are believed to be crucial for channeling gas into the nucleus, the growth of the black hole has the effect of cutting off its own supply of fuel. These models, being based purely on stellar dynamics, have the nice feature that they can be falsified, and in fact they probably have been: our new understanding of black hole demographics (Section 2.3) suggests that few if any galaxies have M / M_bulge as great as 10^-2. (At the time of these studies, several galaxies were believed from ground-based data to have M / M_bulge > 1%, including NGC 1399 (Magorrian et al. 1998), NGC 3115 (Kormendy et al. 1996a), and NGC 4486b (Kormendy et al. 1997)).

The tightness of the M - relation must place strong constraints on the growth of black holes during mergers. We know empirically that mergers manage to keep galaxies on the fundamental plane, which is a relation between , the bulge effective radius R_e and the surface brightness at R_e. The that appears in the fundamental plane relation is the same _c that appears in the M - relation (indeed, it was defined by Ferrarese & Merritt 2000 for just this reason) and furthermore _c is defined within a large enough aperture that it is unlikely to be significantly affected by dynamical processes associated with the formation of a black-hole binary during a merger (Milosavljevic & Merritt 2001). Hence the physics of the black-hole binary can be ignored and we can ask simply: How do mergers manage to grow black holes in such a way that logM 4.5 log, independent of changes in R_e and L?

This work was supported by NSF grant 00-71099 and by NASA grants NAG5-6037 and NAG5-9046. We thank B. Peterson and A. Wandel for useful discussions.