Published in "The Interstellar Medium in Galaxies",
eds. H.A. Thronson, Jr. and J. Michael Shull, 1990 Kluwer Academic
Publishers.
Thermal Phases of the Interstellar Medium in Galaxies
Mitchell C. Begelman
Joint Institute for Laboratory Astrophysics
University of Colorado
and National Institute of Standards and Technology, Boulder, CO
80309-0440
Abstract. This review deals with the theory of multiphase media in
astrophysical systems. I discuss the basic reasons for the existence of
multiple thermal phases, and the
fundamental connection between multiphase media and thermal
instability. After describing
important examples of multiphase media, I examine the interactions among
phases, i.e.,
mass exchange driven by thermal conduction and hydrodynamic
ablation. Mass exchange
may compete with radiative heating and cooling for control of the
thermal state of the hot
phase, and may alter the thermal stability properties of the system.
Table of Contents
 INTRODUCTION
INTRODUCTION
 THEORY OF MULTIPHASE MEDIA
THEORY OF MULTIPHASE MEDIA
 Why thermal phases?
Why thermal phases?
 Connection with thermal instability
Connection with thermal instability
 Examples of thermal phases
Examples of thermal phases
 INTERACTIONS AMONG PHASES
INTERACTIONS AMONG PHASES
 Evaporation and condensation
Evaporation and condensation
 Ablation
Ablation
 Consequences of Mass Exchange
Consequences of Mass Exchange
 Mass exchange vs. radiative heating/cooling
Mass exchange vs. radiative heating/cooling
 Evolution of multiphase systems
Evolution of multiphase systems
 CONCLUSIONS
CONCLUSIONS
 REFERENCES
REFERENCES
1. INTROUCTION
Astrophysical gases are often highly inhomogeneous, with two or more
"thermal phases"
coexisting in rough pressure balance with one another. Compared to the
scales of typical
inhomogeneities, the transitions between neighboring regions of
different temperature (and
density) can be quite sharp. Such systems are most often modeled as
consisting of cold
clouds, filaments or sheets embedded in a hotter intercloud medium,
although there may
be cases in which a model consisting of hot bubbles in a cold matrix is
more appropriate.
Usually the topology of the phases is highly uncertain, but the
conditions which lead to
their existence are more reliably established. The temperatures of the
phases sometimes
differ by orders of magnitude, and are frequently set within rather
narrow ranges by the
details of atomic and molecular processes or by the spectrum of ambient
radiation. It
should be stressed that thermal pressure balance may not be exact,
e.g., where magnetic
fields or cosmic rays supply a significant fraction of the pressure in
one or more phases,
where self-gravity or turbulent pressure are dynamically important,
where ram pressure
(associated with differential motion of the phases) provides part of the
confinement, in the
case of a cool cloud evaporating suprathermally in a hot background
(Balbus and McKee 1982),
or when there is simply too little time for a system to achieve
dynamical equilibrium.
Although the concepts of multiphase media are not generally used to
describe regions which
are wildly out of dynamical equilibrium with their surroundings (such as
material behind
a propagating shock front), localized pressure fluctuations may be an
important means of transferring material between phases
(Wang and Cowie 1988).
This review presents an overview of the theory of thermal phases, with
particular
attention to their role in the interstellar media of galaxies. In
Section 2 I discuss the basic reasons
for the existence of multiphase media, and show the connection between
multiple phases
and thermal instability. I also give examples of multiphase systems
which are important
in astrophysics. Since the phases are in physical contact, it is
unrealistic to treat them as
being isolated from one another. Section 3
deals with the principal interactions among phases,
thermal conduction and ablation. Taking these interactions into account
is particularly
important if one wishes to understand the temporal evolution of
multiphase media; Section 4
deals with the consequences of mass exchange and with evolutionary
models. The "state
of the art" is summarized in Section 5. Much
of the original material presented in this review
was developed in collaboration with C. F. McKee, and is described in
greater detail in
Begelman and McKee (1990).
2. THEORY OF MULTIPHASE MEDIA
2.1. Why thermal phases?
The existence of multiple thermal phases is made possible by the flow of
energy into and out
of a system. Multiple phases do not develop in systems which are
thermodynamically isolated
from their surroundings. If
 (n, T,
xj) is the heating rate per particle and
(n, T,
xj) is the heating rate per particle and
 (n,
T, xj)
is the cooling function, then the equation of thermal equilibrium may be
written
(n,
T, xj)
is the cooling function, then the equation of thermal equilibrium may be
written

| (1)
|
where n is the density of hydrogen nuclei, T is the
temperature, and xj represents the
fractional concentrations of various species,
xj  nj/n. The pressure is given by
p = xtnkT, where xt =
nj/n. The pressure is given by
p = xtnkT, where xt =
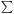 xj is the
number of particles per hydrogen nucleus. An equation analogous
to (1) determines the ionization equilibrium.
xj is the
number of particles per hydrogen nucleus. An equation analogous
to (1) determines the ionization equilibrium.
 , and sometimes
, and sometimes
 (e.g., in the
case of inverse Compton cooling), may also depend on the magnitude of some
external heating or ionization agent, which has energy density
u
(e.g., in the
case of inverse Compton cooling), may also depend on the magnitude of some
external heating or ionization agent, which has energy density
u . If
u
. If
u is held fixed then the solution of the
equilibrium equations generates a curve in the
p - n, p - V (where
V
is held fixed then the solution of the
equilibrium equations generates a curve in the
p - n, p - V (where
V  1/n is
the specific
density) or p - T plane which separates the heating region
(
1/n is
the specific
density) or p - T plane which separates the heating region
( >
n
>
n ) from the
cooling region (
) from the
cooling region ( <
n
<
n ). In
general these curves may have complex shapes and be multivalued.
). In
general these curves may have complex shapes and be multivalued.
If there are two or more values of n (or, equivalently, of
T), which correspond to a
given pressure, then a multiphase equilibrium is possible: a
relatively cool, dense region
can coexist with one or more warmer, less dense regions in pressure
equilibrium. If this configuration is thermally stable (see
Section 2.2 below), and if there
is no mass exchange between
phases, then this equilibrium can persist indefinitely. Simple generic
examples of multiphase
equilibria are shown in Figure 1. In all cases
we have assumed that there is a single stable "cloud" phase with a fixed
temperature Tcl.
Figs. 1 b and 1 d both show systems with
two stable phases, while the other panels show systems with only one
stable phase. More
realistic phase diagrams may show three or more stable phases, e.g.,
Lepp et al. (1985).

|
Figure 1. Radiative thermal equilibrium in
the p - V plane. Cooling exceeds heating above
the solid line. Clouds exist for pressures exceeding
pmin their temperature is fixed at
Tcl.
a) One thermally stable phase. b) Two thermally stable phases separated
by a thermally
unstable phase. c) Thermally stable clouds in a thermally unstable
intercloud medium.
d) If p(V) is multivalued (corresponding to gas at a given
density having one of several
temperatures), the gas may be isochorically as well as isobarically
unstable.
|
In most cases of astrophysical interest,
 is linear in
u
is linear in
u .
If both
.
If both  and
and
 are
independent of density (as in particle or photon heating and two-body
cooling) or depend on density through the ratio n /
u
are
independent of density (as in particle or photon heating and two-body
cooling) or depend on density through the ratio n /
u (as in the case of inverse Compton cooling), then both the
ionization level and the temperature depend on n and
u
(as in the case of inverse Compton cooling), then both the
ionization level and the temperature depend on n and
u only
through the combination n /
u
only
through the combination n /
u or, equivalently, p /
u
or, equivalently, p /
u .
This similarity
variable is very useful for characterizing the
state of gas heated by cosmic rays
(Dalgarno and McCray 1972)
or radiation (e.g.,
Tarter, Tucker and Salpeter 1969;
Davidson 1972;
Krolik, McKee and Tarter 1981);
in various forms it is referred to as the ionization parameter.
.
This similarity
variable is very useful for characterizing the
state of gas heated by cosmic rays
(Dalgarno and McCray 1972)
or radiation (e.g.,
Tarter, Tucker and Salpeter 1969;
Davidson 1972;
Krolik, McKee and Tarter 1981);
in various forms it is referred to as the ionization parameter.
Not all thermal phases which are observed in astrophysical systems
correspond to stable
equilibria. Examples of systems which exhibit long-lived non-equilibrium
hot phases, in pressure balance with a stable cold phase, are the
three-phase interstellar medium
(McKee and Ostriker 1977)
and cooling flows in clusters of galaxies
(Sarazin 1986,
and references therein). The non-equilibrium phases in these systems are
in fact thermally unstable, and
are observable only because their cooling time scales are extremely long
(Spitzer 1956).
An accurate analysis of such systems requires the treatment of
time-dependence
(McKee and Ostriker 1977)
and hydrodynamical effects such as buoyancy
(Balbus and Soker 1989).
2.2. Connection with thermal instability
There is an intimate connection between the existence of thermal phases
and the thermal
stability of a system: any system exhibiting multiphase equilibria must
be thermally
unstable over a range of thermodynamic parameters. The thermal stability
of astrophysical
gases was first studied systematically by Field (1965). His instability
criterion was
generalized to non-equilibrium systems by Balbus (1986 a), who
found the following condition for instability:

| (2)
|
Here s is the entropy per hydrogen nucleus and A is some
thermodynamic variable which
is held constant during the perturbation. In equilibrium,
 = 0 and this reduces
to Field's instability criterion
= 0 and this reduces
to Field's instability criterion

| (3)
|
In general, s is a complicated function of n, T,
and the state of ionization of the
gas. However, in many applications the gas is almost completely ionized
and the entropy
function may be approximated by the expression for an ideal gas,
s ~ lnpV5/3 + const. If
A is some power law combination of p and V, then
T( s /
s /
 T)A
is a constant specific heat which is positive for cases of interest. The
instability criterion then becomes
T)A
is a constant specific heat which is positive for cases of interest. The
instability criterion then becomes

| (4)
|
Since the cooling time is proportional to
T / n , this
criterion can be rephrased as stating
that instability occurs if the cooling time increases with temperature
(Balbus 1986a).
, this
criterion can be rephrased as stating
that instability occurs if the cooling time increases with temperature
(Balbus 1986a).
If the gas is in equilibrium
( = 0), the instability
criterion (4) reduces to
= 0), the instability
criterion (4) reduces to

| (5)
|
Field (1965) showed that for the equilibrium case the isobaric criterion
(
 /
/
 T)p
< 0 is
usually the correct one to apply. However, if the system is large enough
that the sound
crossing time is long compared to the heating or cooling times, then for
long wavelengths the isochoric criterion
(
T)p
< 0 is
usually the correct one to apply. However, if the system is large enough
that the sound
crossing time is long compared to the heating or cooling times, then for
long wavelengths the isochoric criterion
(
 /
/
 T)V
< 0 is applicable.
T)V
< 0 is applicable.
The stability criterion (5) may be interpreted geometrically in terms of
the equilibrium
curve (Figure 1). Typically the
cooling region
(n >
>
 )
lies above the heating region
because the cooling rate usually increases faster with n and
T than does the heating rate.
If, on the other hand, the heating region lay above the cooling region,
then over much of the
curve (wherever p(V) is single-valued) one would have
(
)
lies above the heating region
because the cooling rate usually increases faster with n and
T than does the heating rate.
If, on the other hand, the heating region lay above the cooling region,
then over much of the
curve (wherever p(V) is single-valued) one would have
(
 /
/
 T)V < 0 and the equilibrium
would be isochorically unstable. In this case systems large enough that
the sound crossing
time is much greater than the heating and cooling times could be
unstable even where
smaller systems are isobarically stable. This situation does not arise
in practice and we
therefore assume that the cooling region lies above the heating region
in the p - V plane, as shown in
Figure 1.
T)V < 0 and the equilibrium
would be isochorically unstable. In this case systems large enough that
the sound crossing
time is much greater than the heating and cooling times could be
unstable even where
smaller systems are isobarically stable. This situation does not arise
in practice and we
therefore assume that the cooling region lies above the heating region
in the p - V plane, as shown in
Figure 1.
The slope of the equilibrium curve in the p - V plane is
directly related to the stability of the system since

| (6)
|
(Field 1965).
For cases in which p(V) is single valued (as in
Fig. 1 a-c), the condition
that the cooling region lie above the heating region implies that the
system is isochorically
stable, so that the denominator in equation (6) is positive; hence, in
this case isobarically
stable regions have a negative slope in the p - V plane,
whereas unstable regions have a
positive slope. The condition for a multiphase equilibrium is that
V(p) be a multivalued
function, which is equivalent to having
d lnp / d ln V change
sign. Thus, a necessary and
sufficient condition for the existence of a multiphase equilibrium is
that the system be
thermally unstable over a finite range of V. This proves the
assertion at the beginning of
this section. Fig. 1 d
illustrates a case in which p(V) is
multivalued over a range in V. Such
a system can exhibit both isochoric and isobaric instability, where the
equilibrium curve
has a negative slope in the p - V plane.
A system with two stable phases (e.g.,
Fig. 1b) may be used to
illustrate the inevitability
of multiple phases under certain circumstances. A characteristic feature
of two-phase
systems is that the cold phase cannot exist below some minimum pressure
pmin, while the
hot phase cannot exist above some maximum pressure
pmax. The condition that there be
two stable phases implies that
pmax > pmin. Now consider
a homogeneous system with a density
n1 <  < n2, as shown in
Fig. 2a. Such a system is clearly
unstable in its
homogeneous state. However, it is always possible to stabilize the
system by making it
inhomogeneous, while keeping the mean density constant
(Fig. 2b). The trick is to put
most of the mass in the cold phase, with density
nc > n2,
while a small fraction of the
matter forms a hot intercloud medium, with density
nh < n1 and
temperature Th. Pressure balance requires
nc / nh = Th /
Tcl. If f is the filling factor in cold gas,
then the mean density constraint is
< n2, as shown in
Fig. 2a. Such a system is clearly
unstable in its
homogeneous state. However, it is always possible to stabilize the
system by making it
inhomogeneous, while keeping the mean density constant
(Fig. 2b). The trick is to put
most of the mass in the cold phase, with density
nc > n2,
while a small fraction of the
matter forms a hot intercloud medium, with density
nh < n1 and
temperature Th. Pressure balance requires
nc / nh = Th /
Tcl. If f is the filling factor in cold gas,
then the mean density constraint is
 = (1 -
f)nh + fnc, and
f satisfies
Tcl / Th << f <<
1 if n1 <<
= (1 -
f)nh + fnc, and
f satisfies
Tcl / Th << f <<
1 if n1 <<
 <<
n2.
<<
n2.

|
Figure 2. Inevitability of thermal
instability in a system with a fixed
mean density  and
variable pressure p. Equilibrium curve is identical to that in
Fig. 1b. a) Homogeneous
state is thermally unstable. b) In the stable two-phase state, most of
the mass is in the cold phase with
nc > n2 and a small filling factor. and
variable pressure p. Equilibrium curve is identical to that in
Fig. 1b. a) Homogeneous
state is thermally unstable. b) In the stable two-phase state, most of
the mass is in the cold phase with
nc > n2 and a small filling factor.
|
2.3. Examples of thermal phases
Field, Goldsmith and Habing (FGH: 1969)
produced the first specific
model for a two-phase
equilibrium of the interstellar medium (ISM), in which radiative cooling
is balanced
by cosmic ray heating. The two phases in the FGH model include cold
clouds (T ~ 100 K) and a warm intercloud medium (T ~
104 K). Other heating mechanisms which may be
important (probably more important than cosmic rays
[Spitzer 1978])
include diffuse UV and X-ray flux, photoelectric emission by normal grains
(Draine 1978;
de Jong 1980;
Shull and Woods 1985)
or polycyclic aromatic hydrocarbons (PAHs:
d'Hendecourt and Leger 1987;
Lepp and Dalgarno 1988),
mechanical heating
(Cox 1979),
magnetoacoustic waves
(Spitzer 1982;
Ikeuchi and Spitzer 1984),
and ion-neutral friction
(Scalo 1977; Ferrière,
Zweibel and Shull 1988).
The characteristic temperatures of the warm and cold thermal
phases are insensitive to the details of the heating processes; they
simply reflect the energies
of the resonance and fine-structure lines, respectively, responsible for
cooling the gas. Gas
at ~ 104 K may exist in a range of ionization states, and
McKee and Ostriker (1977)
drew a distinction between the "warm neutral medium" and a "warm
(photo)ionized medium"
irradiated by UV from hot stars. A molecular phase at ~ 10 K is now
known to contain most of the mass in the ISM of the Milky Way, but this
component appears to form
self-gravitating clouds which are out of pressure balance with the rest
of the ISM. A phase diagram for these phases is computed by
Lepp et al. (1985).
The gas which emits the broad emission lines in AGN has also been
modeled as part of a stable two-phase medium
(McCray 1979;
Krolik, McKee, and Tarter 1981
[KMT];
Lepp et al. 1985;
Krolik 1988).
On the basis of observations, the line-emitting gas is
inferred to be concentrated in many small clouds which fill a tiny
fraction of the volume of the emission line region
(Davidson 1972).
Compton heating by the observed X-rays
provides the minimum level of heating of the hot component of the
medium; additional
heating due to relativistic particles, radio frequency heating, cloud
friction, and shocks
may also be important (KMT). Cooling of the hot phase be homogeneous
and hot or in two phases; and finally, there is
usually a range of densities for which the gas must be in two
phases (cf. Fig. 2 and
Section 2.2).
KMT showed that unless the temperature of the hot gas in the broad line
region is well
above 108 K, most of the mass is in the hot phase,
corresponding to the hot/two-phase case.
Cox and Smith (1974)
pointed out that the cooling time of interstellar gas
shock-heated by supernova remnants could be longer than the interval
between the passage of
successive shocks. This suggestion led to the three-phase model of the
ISM (McKee and Ostriker 1977),
in which most of the volume is occupied by shock-heated
gas. This ~ 106 K
gas is an example of a non-equilibrium phase, the possibility of which
was foreseen by
Spitzer (1956).
Because it is produced dynamically, and has a
temperature of order the
virial temperature of the Galaxy, it has proven very difficult to
determine the fate of the
hot intercloud medium. It is not at all clear whether it cools
radiatively in a region close to the disk
(McKee and Ostriker 1977)
or is vented into the halo through "chimneys"
(McCray and Kafatos 1987;
Norman and Ikeuchi 1989),
where it undergoes a combination
of adiabatic and radiative cooling (the "Galactic fountain":
Shapiro and Field 1976;
Cox 1981;
Wang and Cowie 1988).
It is also not known whether the hot gas cools sufficiently in
the halo to form clouds which eventually rain down on the disk, remains
hot enough to drive
a galactic wind, or somehow does both. Finally, the effects of spatial
correlations among
Type II supernovae (in OB associations) are just beginning to be appreciated
(McCray and Kafatos 1987).
Cooling flows in elliptical galaxies and galaxy clusters are also
thought to have a
nonequilibrium two-phase structure. When the existence of cooling flows
was first recognized
(Cowie and Binney 1977;
Fabian and Nulsen 1977),
it was pointed out that the
cooling gas should be thermally unstable to the formation of cool
(~ 104 K) filaments
(Fabian and Nulsen 1977;
Mathews and Bregman 1978;
Cowie, Fabian and Nulsen 1980).
Optical emission lines have been observed in the central regions of many
cooling flows
(Lynds 1970;
Heckman 1981;
Cowie et al. 1983;
Ru, Cowie and Wang 1985;
Johnstone, Fabian and Nulsen 1987;
Heckman et al. 1989).
However, the development of linear thermal
instability is severely hampered by buoyancy
(Balbus 1988;
Balbus and Soker 1989),
and it is not clear whether the filaments grow from finite but small
perturbations or are advected inward in a highly nonlinear form
(Nulsen 1986).
Furthermore, the mechanism
which excites the emission lines is very uncertain, and may play a role
creating and
maintaining the multiphase structure. Multiphase models of cooling flows
have been studied
by Nulsen (1986);
Thomas, Fabian and Nulsen (1987);
Thomas (1988); and
Böhringer and Fabian (1989).
An extreme version of the cooling flow instability has been proposed to
account for
the masses of protogalaxies
(Rees and Ostriker 1977;
Silk 1977)
and of globular clusters
(Fall and Rees 1985).
The basic idea of these models is that a self-gravitating gas cloud
will fragment only when its cooling time becomes shorter than its
free-fall time, and then
it will develop a two-phase structure in which just enough material
drops out of the hot
phase to keep the cooling time roughly comparable to the free-fall
time. Characteristic
mass scales are determined by the Jeans mass of the cold phase in
pressure balance with
the hot phase. Triggering of star formation by radio lobes expanding
into a protogalactic multiphase medium has been proposed
(Rees 1989;
Begelman and Cioffi 1989)
to account for the observed radio/optical alignments in high-redshift radio
galaxies
(McCarthy et al. 1987;
Chambers, Miley and van Breugel 1987).
Cool gas in the multiphase protogalactic
environment might give rise to some quasar absorption line systems
(Hogan 1987)
as well as the extended emission-line "fuzz" around high-redshift quasars
(Rees 1988).
3. INTERACTIONS AMONG PHASES
3.1. Evaporation and condensation
Thermal conduction tries to destroy multiphase structure by erasing
temperature
gradients. Whether this tendency toward homogenization leads to
evaporation of clouds or
the condensation of hot phase onto existing clouds depends on the
cooling function in the
hot phase, as well as the sizes and distribution of clouds. The
efficiency of thermal
conduction also depends on the magnetic connectivity between the phases,
which is poorly
understood. Although the conductivity perpendicular to a magnetic field
line is almost
completely suppressed, any connection between the phases, albeit by
tangled field lines,
is likely to suppress the conductivity only by a factor of a few
(Tribble 1989).
In a fully
ionized cosmic plasma the "classical" coefficient of conductivity is

| (7)
|
(Spitzer 1962;
Draine and Giuliani 1984),
where the factor  c
c
 1 allows for a reduction in
the mean free path due to magnetic fields or turbulence. Equation (7) is
appropriate when
the electron mean free path is sufficiently short compared to
T / |
1 allows for a reduction in
the mean free path due to magnetic fields or turbulence. Equation (7) is
appropriate when
the electron mean free path is sufficiently short compared to
T / | T|
that heat conduction can be treated in the diffusion approximation,
T|
that heat conduction can be treated in the diffusion approximation,
 =
-
=
-
 T. When the
diffusion approximation breaks down, the conductive heat flux first
enters the saturated regime
(Cowie and McKee 1977),
qsat =
5
T. When the
diffusion approximation breaks down, the conductive heat flux first
enters the saturated regime
(Cowie and McKee 1977),
qsat =
5 s
cs p (where cs = (p /
s
cs p (where cs = (p /
 )1/2
is the isothermal sound speed in the intercloud medium and
)1/2
is the isothermal sound speed in the intercloud medium and
 s is a
suppression factor similar to
s is a
suppression factor similar to
 c), and
eventually the "suprathermal" regime
(Balbus and McKee 1982),
in which thermal conduction is best treated by a two-fluid approach.
c), and
eventually the "suprathermal" regime
(Balbus and McKee 1982),
in which thermal conduction is best treated by a two-fluid approach.
The inhibition of multiphase structure by thermal conduction was first
discussed by
Field (1965),
who found that conduction suppresses thermal instability
for wavelengths shorter than a critical value which
Begelman and McKee (1990)
have generalized and dubbed the Field length,

| (8)
|
where  M
M
 Max(
Max( ,
,
 / n).
/ n).
 F is
the maximum length scale across which thermal
conduction can dominate over radiative heating and cooling. Therefore,
the thickness of a
conductive interface with a radius of curvature rc is
~ min(
F is
the maximum length scale across which thermal
conduction can dominate over radiative heating and cooling. Therefore,
the thickness of a
conductive interface with a radius of curvature rc is
~ min( F,
rc)
(McKee and Cowie 1977).
This implies that conduction into clouds with radii smaller than
F,
rc)
(McKee and Cowie 1977).
This implies that conduction into clouds with radii smaller than
 F is
unaffected by heating and cooling processes in the surrounding
medium. Such "small" clouds always evaporate
(Graham and Langer 1973;
Cowie and McKee 1977),
at a rate given by
F is
unaffected by heating and cooling processes in the surrounding
medium. Such "small" clouds always evaporate
(Graham and Langer 1973;
Cowie and McKee 1977),
at a rate given by

| (9)
|
in the classical conduction limit. Clouds with radii larger than
 F have
conductive interfaces whose structures are independent of the cloud
size; such interfaces are dominated by
the balance between conduction and heating/cooling, and may be treated
as plane-parallel.
F have
conductive interfaces whose structures are independent of the cloud
size; such interfaces are dominated by
the balance between conduction and heating/cooling, and may be treated
as plane-parallel.
Steady plane-parallel conduction fronts have been analyzed by
Zel'dovich and Pikel'ner (1969),
Penston and Brown (1970),
and McKee and Begelman (1990).
Ballet, Arnaud and Rothenflug (1986)
and Böhringer and Hartquist (1987)
studied non-equilibrium ionization
in steady evaporative flows. Time-dependent mass exchange has been
analyzed in one dimension by
Doroshkevich and Zel'dovich (1981),
by Balbus (1986b),
who included magnetic fields, and by
Borkowski, Balbus and Fristrom (1989)
who also studied the ionization
structure. If the hot phase is cooling (and is thermally unstable) then
a cooling wave of
fixed thickness propagates into the hot gas following an evaporative
transi
Böhringer and Fabian 1989)
used this result to argue that steady-state
evaporation solutions are incorrect, i.e., that all clouds embedded in a
cooling background
medium should condense, not evaporate. However, the evaporative
transient lasts until
the temperature gradient relaxes to the Field length, and the timescale
for this to occur is the cooling time. The evaporative solutions found by
Cowie and McKee (1977)
persist over a time scale which is short compared to the cooling time,
but long compared to the
time required to set up the evaporation flow. If the hot phase is
thermally stable, then
there exists a "saturated vapor pressure"
psat above which "large" clouds condense, and
below which they evaporate
(Penston and Brown 1970).
Zel'dovich and Pikel'ner (1969)
devised an approximate method for calculating the evaporation rate when
p  psat, which was refined and generalized to spherical
clouds by
McKee and Begelman (1990).
psat, which was refined and generalized to spherical
clouds by
McKee and Begelman (1990).
3.2. Ablation
The motion of clouds with respect to the ambient hot medium leads to
Kelvin-Helrnholtz
and Rayleigh-Taylor instabilities, which can break up the clouds into
smaller pieces and
accelerate mass exchange between the phases. Both instabilities operate
on time scales ti ~
( c
/
c
/  h)1/2 rc /
v, where v is
the relative speed between the cloud and the hot medium and
h)1/2 rc /
v, where v is
the relative speed between the cloud and the hot medium and
 c /
c /
 h
~ Th/Tc in pressure
equilibrium. Most studies have concentrated on the fate
of a cloud overtaken by a strong supernova or spiral density-wave shock
(Woodward 1976;
Nittman, Falle and Gaskell 1982;
Heathcote and Brand 1983;
McKee 1988;
Klein, McKee and Colella 1989).
in this case ti is of the same order as the
"cloud-crushing" time, tcc,
which is the time scale required for a secondary shock to be driven into
a cloud once it is overrun by the main shock
(McKee 1988).
The cloud destruction process is accelerated by
the significant pressure differential between the sides of the cloud and
its front and back
(Nittman, Falle and Gaskell 1982).
The unbalanced forces cause the cloud to "pancake",
i.e., to spread sideways, and the increase in cross-section speeds up
the momentum
deposition which tears apart the cloud. Pressure fluctuations and
vorticity generation arising
from the interactions of multiple shocks also play an important role in
cloud disruption
(Klein, McKee and Colella 1989).
h
~ Th/Tc in pressure
equilibrium. Most studies have concentrated on the fate
of a cloud overtaken by a strong supernova or spiral density-wave shock
(Woodward 1976;
Nittman, Falle and Gaskell 1982;
Heathcote and Brand 1983;
McKee 1988;
Klein, McKee and Colella 1989).
in this case ti is of the same order as the
"cloud-crushing" time, tcc,
which is the time scale required for a secondary shock to be driven into
a cloud once it is overrun by the main shock
(McKee 1988).
The cloud destruction process is accelerated by
the significant pressure differential between the sides of the cloud and
its front and back
(Nittman, Falle and Gaskell 1982).
The unbalanced forces cause the cloud to "pancake",
i.e., to spread sideways, and the increase in cross-section speeds up
the momentum
deposition which tears apart the cloud. Pressure fluctuations and
vorticity generation arising
from the interactions of multiple shocks also play an important role in
cloud disruption
(Klein, McKee and Colella 1989).
The time scale for ablated cloud material to be effectively mixed with
the intercloud
medium should lie somewhere between ti and the
hydrodynamic drag time, td ~
( c
/
c
/  h)
rc/v.
Nulsen (1982),
using the
longer time scale td, estimated that cold gas would
be ablated from a cloud at a rate
h)
rc/v.
Nulsen (1982),
using the
longer time scale td, estimated that cold gas would
be ablated from a cloud at a rate
 ab ~
ab ~
 r2c
r2c
 h
v. If thermal conduction were negligible,
the cloud would leave behind a cylindrical "trail" with a radius
~ rc, containing cold material with a mean density
<
h
v. If thermal conduction were negligible,
the cloud would leave behind a cylindrical "trail" with a radius
~ rc, containing cold material with a mean density
< >tr ~
>tr ~
 h.
If the ablated gas is well-mixed with the hot phase
downstream of the cloud, as we might expect from a turbulent ablation
process, then the
global time scale for cooling the hot phase by ablation is simply the
time required for the trails to fill space,
tab ~ rc /
h.
If the ablated gas is well-mixed with the hot phase
downstream of the cloud, as we might expect from a turbulent ablation
process, then the
global time scale for cooling the hot phase by ablation is simply the
time required for the trails to fill space,
tab ~ rc /
 fv, where f
is the filling factor in clouds.
tab is shorter than the cloud
disruption time if the clouds contain more mass than the hot phase, and
it is longer than the saturated evaporation time by a f actor
~
fv, where f
is the filling factor in clouds.
tab is shorter than the cloud
disruption time if the clouds contain more mass than the hot phase, and
it is longer than the saturated evaporation time by a f actor
~  -1,
where
-1,
where  is the Mach
number of cloud motion relative to the hot phase.
is the Mach
number of cloud motion relative to the hot phase.
For diffuse interstellar clouds moving through the hot phase of the ISM
in the Milky Way,
 ~ 0.1.
According to the
Nulsen (1982)
model, ablation from subsonically moving
clouds is a less important mechanism for destroying clouds than
conduction in the
saturated limit, but may be more important than conduction in the
classical limit, i.e.,
for large clouds. For clouds moving nearly sonically, e.g., randomly
moving clouds in the
spheroidal component of a galaxy, hydrodynamical instabilities are
probably the most
efficient mechanism for shredding clouds to the point where thermal
mixing via conduction is very efficient.
~ 0.1.
According to the
Nulsen (1982)
model, ablation from subsonically moving
clouds is a less important mechanism for destroying clouds than
conduction in the
saturated limit, but may be more important than conduction in the
classical limit, i.e.,
for large clouds. For clouds moving nearly sonically, e.g., randomly
moving clouds in the
spheroidal component of a galaxy, hydrodynamical instabilities are
probably the most
efficient mechanism for shredding clouds to the point where thermal
mixing via conduction is very efficient.
Lateral expansion of the cloud can shorten the hydrodynamic drag time
considerably
(Nittman, Falle and Gaskell 1982;
Klein, McKee and Colella 1989).
Klein, McKee and
Colella find that the drag time is of order ti for
density contrasts
 c /
c /
 h
as high as 100, but
for much larger density contrasts the cloud is torn apart before it
slows significantly. These
calculations suggest that mixing can occur much more rapidly than
predicted by the
Nulsen (1982)
model. Further numerical simulations capable of following the
mixing process with
high resolution are clearly needed to test the basic assumptions of any
ablation model.
h
as high as 100, but
for much larger density contrasts the cloud is torn apart before it
slows significantly. These
calculations suggest that mixing can occur much more rapidly than
predicted by the
Nulsen (1982)
model. Further numerical simulations capable of following the
mixing process with
high resolution are clearly needed to test the basic assumptions of any
ablation model.
4. CONSEQUENCES OF MASS EXCHANGE
4.1. Mass exchange vs. radiative heating/cooling
When the bulk of the energy content and the bulk of the mass content
reside in different
phases, a relatively small amount of mass or energy transfer between
phases can have a
large effect on the structure of a multiphase medium. Such a situation
is believed to exist in the three-phase model of the ISM
(McKee and Ostriker 1977),
where the hot phase
occupies most of the volume while most of the mass is in cold
clouds. Physically, the effect
of mass exchange (either by conduction or ablation followed by effective
mixing) is to cool
the hot phase, since a fixed amount of energy is being distributed among
a larger number
of particles. Since radiative heating and cooling depend on both density
and temperature,
mass exchange can affect the radiative evolution of the medium as
well. We can illustrate
the global consequences of mass and energy exchange between phases by
considering a
medium with uniform pressure and subsonic motions, in which mass
exchange is driven by
thermal conduction. The approximate time-dependent equations governing
the medium are then
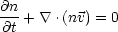
| (10)
|
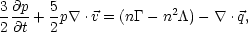
| (11)
|
where  represents
the conductive heat flux. Note that these equations are appropriate
in the single-fluid limit, corresponding to classical or mildly
saturated conduction
(Cowie and McKee 1977):
in the highly saturated suprathermal limit
(Balbus and McKee 1982),
both the single-fluid approximation and the assumption of pressure
balance break down.
The evolution of the medium is driven by the terms on the
right-hand-side of eq. (11), and
may be dominated either by the effects of conduction or by the effects
of radiative heating and cooling.
represents
the conductive heat flux. Note that these equations are appropriate
in the single-fluid limit, corresponding to classical or mildly
saturated conduction
(Cowie and McKee 1977):
in the highly saturated suprathermal limit
(Balbus and McKee 1982),
both the single-fluid approximation and the assumption of pressure
balance break down.
The evolution of the medium is driven by the terms on the
right-hand-side of eq. (11), and
may be dominated either by the effects of conduction or by the effects
of radiative heating and cooling.
There is a crucial distinction between the heat flux term and the
radiative loss term in
the energy equation: the energy entering or leaving a volume of radius
r due to conduction is proportional to r2
q( r
for classical conduction) whereas that due to heating or cooling
is proportional to r3. Thus, there is a critical
length scale which enters the problem, which
turns out to be the Field length,
r
for classical conduction) whereas that due to heating or cooling
is proportional to r3. Thus, there is a critical
length scale which enters the problem, which
turns out to be the Field length,
 F
(eq. [8]), when mass exchange is driven by classical conduction.
F
(eq. [8]), when mass exchange is driven by classical conduction.
The temperature structure of the intercloud medium in a system of clouds
extending
over a region of size R depends on the ratio of the Field length to
R.
Balbus (1985)
developed an elegant electrostatic analogy for an ensemble of clouds in
a hot intercloud
medium under conditions in which radiative heating and cooling are
negligible and the
temperature is specified on the boundary of the ensemble. This
corresponds to the case R <<
 F. In a
steady state, the
evaporation rate and the temperature structure in the intercloud
medium are then determined by a solution of Laplace's equation with
Dirichlet boundary
conditions. In the complementary case, R >>
F. In a
steady state, the
evaporation rate and the temperature structure in the intercloud
medium are then determined by a solution of Laplace's equation with
Dirichlet boundary
conditions. In the complementary case, R >>
 F, global heat
flows are insignificant and
the temperature structure of the intercloud gas is determined by a
competition between
cloud evaporation on the one hand and heating and cooling on the
other. Numerically, the Field length is
F, global heat
flows are insignificant and
the temperature structure of the intercloud gas is determined by a
competition between
cloud evaporation on the one hand and heating and cooling on the
other. Numerically, the Field length is
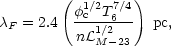
| (12)
|
where T6
 T/106
K and
T/106
K and  M-23
M-23

 M /
(10-23 erg cm3 s-1) is normalized to a
characteristic value of the radiative cooling rate for astrophysical
plasmas.
M /
(10-23 erg cm3 s-1) is normalized to a
characteristic value of the radiative cooling rate for astrophysical
plasmas.
To quantify the competition between mass exchange and radiative
heating/cooling,
consider the spatially averaged effect of cloud evaporation on the hot
phase. This is
meaningful only when the characteristic temperature of the hot phase
changes over a length
scale which exceeds the mean intercloud separation
r0. This condition is guaranteed to be
satisfied when r0 is smaller than
 F. When
r0 exceeds
F. When
r0 exceeds
 F, then
mass exchange cannot compete with radiative heating and cooling anyway,
so the point is moot. If there are
ncl(
F, then
mass exchange cannot compete with radiative heating and cooling anyway,
so the point is moot. If there are
ncl( 3/4
3/4 r30) clouds per unit volume
evaporating at a mean rate
r30) clouds per unit volume
evaporating at a mean rate
 ev per
cloud, then the density of the intercloud medium changes at a rate
ev per
cloud, then the density of the intercloud medium changes at a rate

| (13)
|
where  ev is
negative for condensation. We may then use
ev is
negative for condensation. We may then use
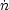 ev to define an
effective evaporative cooling rate,
ev to define an
effective evaporative cooling rate,
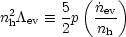
| (14)
|
(Begelman and McKee 1990).
The evaporative cooling coefficient
 ev is
analogous to the radiative cooling coefficient
ev is
analogous to the radiative cooling coefficient
 in that both
reduce the specific entropy s, but there are
crucial differences between the two:
in that both
reduce the specific entropy s, but there are
crucial differences between the two:
 reduces the total
entropy of a given volume of intercloud gas, whereas
reduces the total
entropy of a given volume of intercloud gas, whereas
 ev
increases it;
ev
increases it;  reduces the energy density of the intercloud gas, whereas
reduces the energy density of the intercloud gas, whereas
 ev
leaves it unchanged. Because of these distinctions,
ev
leaves it unchanged. Because of these distinctions,
 ev
should not be included in the net radiative cooling function
ev
should not be included in the net radiative cooling function
 . However, the relative
impact of mass exchange and
radiative heating/cooling on the thermal state of the intercloud medium
can be expressed by the radiation/evaporation ratio
(Begelman and McKee 1990),
. However, the relative
impact of mass exchange and
radiative heating/cooling on the thermal state of the intercloud medium
can be expressed by the radiation/evaporation ratio
(Begelman and McKee 1990),
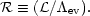
| (15)
|
When  M
M

 M /
M /
 ev is
>> 1( << 1), then radiative heating and cooling (mass exchange)
determines the thermal state of the intercloud medium.
ev is
>> 1( << 1), then radiative heating and cooling (mass exchange)
determines the thermal state of the intercloud medium.
One can express  in
terms of quantities which characterize the structure of the
two-phase medium. Writing the evaporation rate in the form
in
terms of quantities which characterize the structure of the
two-phase medium. Writing the evaporation rate in the form
 ev =
4
ev =
4 r2c
r2c
 h
csf, where cs
is the isothermal sound speed in the hot phase, we have
h
csf, where cs
is the isothermal sound speed in the hot phase, we have
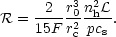
| (16)
|
r0 may be eliminated in favor of the cloud filling
factor f (assumed to be << 1) by substituting
rc/f for
r03 / rc2. In
the limit of saturated evaporation F ~ a few
(Cowie and McKee 1977),
while
F ~  / 4 in the
Nulsen (1982)
model of ablation. In the classical conduction
limit, F is twice the "saturation parameter"
/ 4 in the
Nulsen (1982)
model of ablation. In the classical conduction
limit, F is twice the "saturation parameter"
 '0 derived by
Cowie and McKee (1977),
with the result that
'0 derived by
Cowie and McKee (1977),
with the result that

| (17)
|
Cloud evaporation thus determines the intercloud temperature for
rc > r30 /
 F2.
The corresponding condition on the filling factor is
F2.
The corresponding condition on the filling factor is
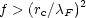
| (18)
|
or f > (r0 /
 F)6;
for f ~ 0.03, as in the ISM, this will
be true if
F)6;
for f ~ 0.03, as in the ISM, this will
be true if  F
F
 2r0. In terms of the
sound-crossing time across rc (measured in the hot phase),
ts ~ rc / 2cs, and
the radiative cooling time in the hot phase,
tc ~ 5kTh / 2nh
2r0. In terms of the
sound-crossing time across rc (measured in the hot phase),
ts ~ rc / 2cs, and
the radiative cooling time in the hot phase,
tc ~ 5kTh / 2nh
 (Th)
, we may express the condition for mass
exchange to dominate globally in the form
(Th)
, we may express the condition for mass
exchange to dominate globally in the form

| (19)
|
Writing (18) in the form
r0 < r1/3c
 F2/3,
we see that the intercloud spacing in a
conduction-dominated medium must also be smaller than the Field
length. This has
important consequences for the thermal stability of the hot phase in a
conduction-dominated system. Since
F2/3,
we see that the intercloud spacing in a
conduction-dominated medium must also be smaller than the Field
length. This has
important consequences for the thermal stability of the hot phase in a
conduction-dominated system. Since
 F is
roughly the minimum wavelength which is thermally unstable
(Field 1965),
potentially unstable regions must contain many clouds. The
conduction-modified
condition for thermal instability is obtained simply by including
F is
roughly the minimum wavelength which is thermally unstable
(Field 1965),
potentially unstable regions must contain many clouds. The
conduction-modified
condition for thermal instability is obtained simply by including
 ev
in Balbus's (1986a)
criterion (eq. [4]):
ev
in Balbus's (1986a)
criterion (eq. [4]):

| (20)
|
(Begelman and McKee 1990).
nh
 ev /
Th is
generally an increasing function of Th: for
isobaric perturbations nh
ev /
Th is
generally an increasing function of Th: for
isobaric perturbations nh
 ev /
Th ~ q
ev /
Th ~ q
 Th7/2(Th1/2)
for classical (saturated) conduction.
Therefore, evaporation has a stabilizing influence on the hot
phase, and in a
conduction-dominated medium thermal instability will be inhibited by the
presence of evaporating clouds
(Begelman and McKee 1990).
This will be true even if the radiative processes place
the hot phase in a thermally unstable regime. However, it should be
noted that the cooling
time scale in the hot phase of a conduction-dominated medium is shorter
than the radiative
cooling time scale. Therefore, conduction cannot stabilize a hot phase
over a time scale
which is longer than the time scale for radiative thermal
instability. However, it can lead
to the hot phase cooling down somewhat before the onset of thermal
instability. Since
thermal conduction generally becomes less important at low temperatures,
such a system
may evolve to a state in which evaporative cooling no longer dominates,
whereupon thermal
instability may occur. Since the Field length is generally a strongly
increasing function of
temperature, the operation of thermal instability may lead to the
production of smaller
and more closely spaced clouds than would have formed in the hotter medium.
Th7/2(Th1/2)
for classical (saturated) conduction.
Therefore, evaporation has a stabilizing influence on the hot
phase, and in a
conduction-dominated medium thermal instability will be inhibited by the
presence of evaporating clouds
(Begelman and McKee 1990).
This will be true even if the radiative processes place
the hot phase in a thermally unstable regime. However, it should be
noted that the cooling
time scale in the hot phase of a conduction-dominated medium is shorter
than the radiative
cooling time scale. Therefore, conduction cannot stabilize a hot phase
over a time scale
which is longer than the time scale for radiative thermal
instability. However, it can lead
to the hot phase cooling down somewhat before the onset of thermal
instability. Since
thermal conduction generally becomes less important at low temperatures,
such a system
may evolve to a state in which evaporative cooling no longer dominates,
whereupon thermal
instability may occur. Since the Field length is generally a strongly
increasing function of
temperature, the operation of thermal instability may lead to the
production of smaller
and more closely spaced clouds than would have formed in the hotter medium.
It is instructive to apply the ideas discussed above to the three-phase
model of the ISM
(McKee and Ostriker 1977).
The three-phase ISM consists of cold HI clouds
surrounded by warm HI and HII envelopes, all embedded in a pervasive hot
ionized medium
(HIM). The physical conditions in the HIM are governed by mass exchange
with the clouds
and energy injection by supernovae. The model is intrinsically
time-dependent: A given
element of gas is compressed and heated by SNRs at intervals of about
5 × 105 yr, and
this makes its evolution difficult to analyze using concepts developed
to treat steady-state
or slowly evolving systems. Nonetheless, it is of interest to evaluate
the Field length and
the radiation/evaporation ratio. Using the fit to the cooling function
of Raymond, Cox and Smith (1976)
for cosmic abundances,
 (T)
(T)
 1.6 ×
10-19T-1/2 erg cm3
s-1 (105 K
< T < 4 × 107 K), multiplied by an
enhancement factor
1.6 ×
10-19T-1/2 erg cm3
s-1 (105 K
< T < 4 × 107 K), multiplied by an
enhancement factor

 10
10 1
1
 10 to take account of
nonequilibrium ionization and density inhomogeneity near conduction fronts
(McKee and Ostriker 1977),
we have
10 to take account of
nonequilibrium ionization and density inhomogeneity near conduction fronts
(McKee and Ostriker 1977),
we have
 F =
44(
F =
44( c1/2
T36 /
c1/2
T36 /
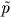 4
4
 11/2) pc, where
11/2) pc, where
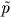 4
4
 p /
104k and
T6
p /
104k and
T6  Th/106 K. We can write condition (18) in
the form
Th/106 K. We can write condition (18) in
the form
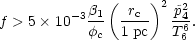
| (21)
|
It is evident that the relative importance of conductive and radiative
energy exchange
is sensitive to conditions in the hot phase, particularly to
Th, as well as to the filling
factor and typical size of clouds. Under the conditions deduced by McKee
and Ostriker
(T6 = 0.45,
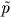 4 = 0.36,
4 = 0.36,
 1
= 1, rc = 2.1
pc, and f = 0.23), condition (21) is marginally
satisfied. Equivalently, the radiation/evaporation ratio is given by
R = 0.38, which implies
that evaporative cooling dominates radiative cooling and that the HIM is
thermally stable.
(The argument that evaporation can stabilize the HIM is originally due
to McCray [1986].)
However, even a small amount of cloud ablation by hydrodynamic processes
(Section 3.2) or a
slight increase in the HIM temperature would lead to a drastic increase
in the energetic
importance of evaporation. If the typical clouds were sufficiently small
that conduction
were saturated, i.e., for
1
= 1, rc = 2.1
pc, and f = 0.23), condition (21) is marginally
satisfied. Equivalently, the radiation/evaporation ratio is given by
R = 0.38, which implies
that evaporative cooling dominates radiative cooling and that the HIM is
thermally stable.
(The argument that evaporation can stabilize the HIM is originally due
to McCray [1986].)
However, even a small amount of cloud ablation by hydrodynamic processes
(Section 3.2) or a
slight increase in the HIM temperature would lead to a drastic increase
in the energetic
importance of evaporation. If the typical clouds were sufficiently small
that conduction
were saturated, i.e., for
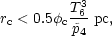
| (22)
|
(Cowie and McKee 1977;
Balbus and McKee 1982),
the appropriate version of condition (19) would be

| (23)
|
In the McKee-Ostriker picture, each region of HIM is overrun by another
supernova remnant before it has time relax to a stationary state with

 1. Stochastic heating
by SNR shocks thus leads to discontinuous trajectories in the p -
V plane, and heating
is balanced by radiative cooling. In the galactic fountain model
(Shapiro and Field 1976;
Wang and Cowie 1988),
the heat is advected into the galactic halo. If clouds are effectively
ablated then the accelerated lowering of Th by
evaporation may allow the large tracts of
the ISM to cool to a homogeneous state at
T
1. Stochastic heating
by SNR shocks thus leads to discontinuous trajectories in the p -
V plane, and heating
is balanced by radiative cooling. In the galactic fountain model
(Shapiro and Field 1976;
Wang and Cowie 1988),
the heat is advected into the galactic halo. If clouds are effectively
ablated then the accelerated lowering of Th by
evaporation may allow the large tracts of
the ISM to cool to a homogeneous state at
T  104 K. The intercloud medium remains
thermally stable until radiative cooling begins to dominate over
evaporative cooling, at Th
104 K. The intercloud medium remains
thermally stable until radiative cooling begins to dominate over
evaporative cooling, at Th
 105
K. Since the Field length is a strongly increasing
function of Th, the onset of
instability at a reduced temperature may lead to the formation of
sub-parsec size clouds.
105
K. Since the Field length is a strongly increasing
function of Th, the onset of
instability at a reduced temperature may lead to the formation of
sub-parsec size clouds.
4.2. Evolution of multiphase systems
By averaging the equations of mass and energy conservation over a volume
(V) which
contains many clouds, one can derive equations for the global evolution
of the hot intercloud medium in the presence of mass exchange with
embedded clouds
(Begelman and McKee 1990).
The mass of intercloud gas in
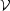 is
is
 h
µH
h
µH
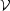 , where
, where
 h is the mean
density of the
intercloud gas in
h is the mean
density of the
intercloud gas in 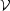 .
Choosing the volume
.
Choosing the volume 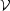 to comove with the intercloud gas implies that
this mass can change only by cloud evaporation, at a rate
to comove with the intercloud gas implies that
this mass can change only by cloud evaporation, at a rate
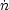 ev
µH
ev
µH
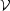 . Mass conservation for
the intercloud gas then becomes
. Mass conservation for
the intercloud gas then becomes

| (24)
|
Integration of equation (11) over
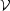 then implies
then implies

| (25)
|
where s is the surface bounding
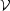 . By assuming that the
characteristic dimension of the
averaging volume is large compared to the Field length, we ensure that
the conductive heat
flux term in equation (25) is negligible compared to the heating and
cooling term. The global energy equation then simplifies to
. By assuming that the
characteristic dimension of the
averaging volume is large compared to the Field length, we ensure that
the conductive heat
flux term in equation (25) is negligible compared to the heating and
cooling term. The global energy equation then simplifies to

| (26)
|
where
< >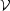 denotes an average over the volume
denotes an average over the volume
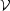 . Note that mass
exchange does not enter
this equation: mass exchange alters the density and temperature of the
intercloud gas, but not its pressure.
. Note that mass
exchange does not enter
this equation: mass exchange alters the density and temperature of the
intercloud gas, but not its pressure.
Additional constraints are required to solve for the evolution of a
specific system.
Since the cloud evaporation rate depends on the typical cloud size, it
is necessary to have
an equation for the evolution of rc in time. There are
also likely to be externally imposed
constraints on the intercloud medium; Begelman and McKee (1990)
considered two limiting
cases. In the isochoric limit, tile comoving volume
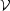 is
held constant as the system evolves.
If one assumes that the clouds are fixed as well, then the mean density
is
held constant as the system evolves.
If one assumes that the clouds are fixed as well, then the mean density
 also remains
constant. This condition would apply in a system in which the sound
crossing time R/cs is
long compared to both the characteristic heating/cooling time and the
evaporation time.
Such a situation might apply locally within a supersonic accretion flow
or wind. Setting
also remains
constant. This condition would apply in a system in which the sound
crossing time R/cs is
long compared to both the characteristic heating/cooling time and the
evaporation time.
Such a situation might apply locally within a supersonic accretion flow
or wind. Setting
 = 0 in
eqs. (24) and (26), we obtain
= 0 in
eqs. (24) and (26), we obtain

| (27)
|
and

| (28)
|
In the isobaric limit, the intercloud medium can exchange mass
with a reservoir in order
to maintain a constant pressure, so we set p(t) =
constant. Such a situation might apply,
for example, if the system were in contact with an X-ray heated wind
above an accretion disk
(Begelman, McKee and Shields 1983).
We then have

| (29)
|
The instantaneous state of the intercloud medium can be described by the
location of a point in the p - V plane (cf.
Fig. 1);
V  n-1h
is the specific volume of the intercloud
gas. The radiative equilibrium curve
n2h
n-1h
is the specific volume of the intercloud
gas. The radiative equilibrium curve
n2h
 = 0
divides the plane into two regions: above
the curve, radiative cooling exceeds the external heating, whereas below
the curve the converse is true. The net cooling rate
n2h
= 0
divides the plane into two regions: above
the curve, radiative cooling exceeds the external heating, whereas below
the curve the converse is true. The net cooling rate
n2h
 may be
assumed to be a known function of p
and V everywhere on the plane. However, the evaporation rate
may be
assumed to be a known function of p
and V everywhere on the plane. However, the evaporation rate
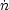 ev also depends
on the distribution of cloud sizes and separations.
ev also depends
on the distribution of cloud sizes and separations.
The character of a trajectory in the p - V plane is
determined by the
relative importance of energy exchange and mass exchange, which is expressed
quantitatively by the radiation/evaporation ratio
 (eq. [16]). in the
isochoric case, the slope of trajectories in
the p - V plane is governed by the ratio of equations (27)
and (28):
(eq. [16]). in the
isochoric case, the slope of trajectories in
the p - V plane is governed by the ratio of equations (27)
and (28):

| (30)
|
Trajectories are nearly vertical if radiative cooling and heating are
dominant
(| | >> 1),
and nearly horizontal if mass exchange is dominant
(|
| >> 1),
and nearly horizontal if mass exchange is dominant
(| | << 1). It
is immediately obvious
that trajectories must be locally horizontal
(dp / dV = 0) where they cross the equilibrium curve
(
| << 1). It
is immediately obvious
that trajectories must be locally horizontal
(dp / dV = 0) where they cross the equilibrium curve
( = 0), provided that
= 0), provided that
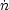 ev
ev
 0 at the
point of crossing. Points at which
0 at the
point of crossing. Points at which
 =
=
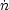 ev = 0
represent stationary states. The temperature evolves as
ev = 0
represent stationary states. The temperature evolves as

| (31)
|
Trajectories with
 = - 3/5 are
isothermal. Isobaric trajectories are constrained to be
horizontal in the p - V plane. The direction (and rate) of
motion is given by equation (29), which may be written in the form
= - 3/5 are
isothermal. Isobaric trajectories are constrained to be
horizontal in the p - V plane. The direction (and rate) of
motion is given by equation (29), which may be written in the form

| (32)
|
Since T  pV
pV
 V in the
isobaric case, this equation also describes the temperature
evolution of the system. The point
V in the
isobaric case, this equation also describes the temperature
evolution of the system. The point
 = - 1 represents a
steady state for the hot phase,
although mass continues to be lost (if
= - 1 represents a
steady state for the hot phase,
although mass continues to be lost (if
 < 0) or gained (if
< 0) or gained (if
 > 0) by clouds in
this state (unlike the "true" steady state
> 0) by clouds in
this state (unlike the "true" steady state
 =
=
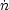 ev = 0
in the isochoric case). For a system
dominated by radiative heating or cooling
(|
ev = 0
in the isochoric case). For a system
dominated by radiative heating or cooling
(| | >> 1),
evolution is leftward above the
thermal equilibrium curve and rightward below the curve. In a system
dominated by mass exchange
(|
| >> 1),
evolution is leftward above the
thermal equilibrium curve and rightward below the curve. In a system
dominated by mass exchange
(| | << 1),
evolution is leftward for evaporation and rightward for condensation.
A more detailed discussion of p - V plane trajectories may
be found in
Begelman and McKee (1990),
who considered the specific case of a gas heated by
Compton scattering and
cooled by bremsstrahlung and the inverse Compton effect. They also
discuss the stability properties of evolving systems.
| << 1),
evolution is leftward for evaporation and rightward for condensation.
A more detailed discussion of p - V plane trajectories may
be found in
Begelman and McKee (1990),
who considered the specific case of a gas heated by
Compton scattering and
cooled by bremsstrahlung and the inverse Compton effect. They also
discuss the stability properties of evolving systems.
5. CONCLUSIONS
Multiple thermal phases are known to exist in many astrophysical
systems. The reasons
for their existence are understood in general terms, but the detailed
properties of specific
multiphase systems are poorly known. We can look forward to the further
development of
multiphase models for the ISM in elliptical galaxies, cooling flows in
clusters of galaxies,
the intergalactic medium, and protogalactic environments. The structures
of multiphase
media are sensitive to the rate of mass exchange between phases, which
tends to lower
the temperature of the hot phase and render it thermally
stable. Unfortunately, mass
exchange through thermal conduction depends on the topology of
conduction fronts and
on the magnetic connectivity of the phases, neither of which is
understood. However,
mixing of the phases may be driven by hydrodynamic instabilities at a
rate much faster
than that due to thermal conduction. Rapidly improving hydrodynamic
codes with a high
dynamic range in spatial resolution (e.g., using an adaptive mesh)
should clarify some of the physics of the ablation process within the
next few years.
ACKNOWLEDGMENTS. Many of the ideas presented above were developed
collaboratively
with C. F. McKee. Portions of the text borrow heavily (and in some cases
verbatim) from Begelman and McKee (1990), which is to be published in
The Astrophysical Journal.
Preparation of this article was supported in part by NSF grant
AST88-16140, NASA
Astrophysical Theory Center grant NAGW-766, and a grant from the Alfred
P. Sloan Foundation.
REFERENCES
-
Balbus, S. A.
1985, Ap. J., 291, 518.
-
Balbus, S. A.
1986a, Ap. J. (Letters), 303, L79.
-
Balbus, S. A.
1986b, Ap. J., 304, 787.
-
Balbus, S. A.
1988, Ap. J., 328, 395.
-
Balbus, S. A., and McKee, C. F.
1982, Ap. J., 252, 529.
-
Balbus, S. A., and Soker, N.
1989, Ap. J., 341, 611.
-
Ballet, J., Arnaud, M., and Rothenflug, R.
1986, Astr. Ap., 161, 12.
-
Begelman, M. C., and Cioffi, D. F.
1989, Ap. J. (Letters),
345, L21.
-
Begelman, M. C., and McKee, C. F.
1990, Ap. J., 358, 375.
-
Begelman, M. C., McKee, C. F., and Shields, G. A.
1983, Ap. J., 271, 70.
-
Böhringer, H., and Fabian, A. C.
1989, M.N.R.A.S., 237, 1147.
-
Böhringer, H., and Hartquist, T. W.
1987, M.N.R.A.S., 228, 915.
-
Borkowski, K. J., Balbus, S. A., and Fristrom, C. C. 1989, preprint.
-
Chambers, K. C., Miley, G. K., and van Breugel, W. J. M.
1987, Nature, 329, 604.
-
Cowie, L. L., and Binney, J.
1977, Ap. J., 215, 723.
-
Cowie, L. L., Fabian, A. C., and Nulsen, P. E. J.
1980, M.N.R.A.S., 191, 399.
-
Cowie, L. L., Hu, E. M., Jenkins, E., and York, D.
1983, Ap. J., 272, 29.
-
Cowie, L. L., and McKee, C. F.
1977, Ap. J., 211, 135.
-
Cox, D. P.
1979, Ap. J., 234, 863.
-
Cox, D. P.
1981, Ap. J., 245, 534.
-
Cox, D. P., and Smith, B. W.
1974, Ap. J. (Letters), 189, L105.
-
Dalgarno, A., and McCray, R. A.
1972, Ann. Rev. Astr. Ap., 10, 375.
-
Davidson, K.
1972, Ap. J., 171, 213.
-
de Jong, T.
1980, Highlights Astr., 5, 301.
-
d'Hendecourt, L. B., and Leger, A.
1987, Astr. Ap., 180, L9.
-
Doroshkevich, A. G., and Zel'dovich, Ya. B.
1981, Sov. Phys. J.E.T.P., 53, 405.
-
Draine, B. T.
1978, Ap. J. Suppl., 36, 595.
-
Draine, B. T., and Giuliani, J. L.
1984, Ap. J., 281, 690.
-
Fabian, A. C., Guilbert, P., Arnaud, K., Shafer, R., Tennant,
A., and Ward, M.
1986, M.N.R.A.S., 218, 457.
-
Fabian, A. C., and Nulsen, P. E. J.
1977, M.N.R.A.S., 180, 479.
-
Fall, S. M., and Rees, M. J.
1985, Ap. J., 298, 18.
-
Ferrière, K. M., Zweibel, E. G., and Shull, J. M.
1988, Ap. J., 332, 984.
-
Field, G. B.
1965, Ap. J., 142, 531.
-
Field, G. B., Goldsmith, D. W., and Habing, H. J.
1969, Ap. J. (Letters), 155, L149 (FGH).
-
Graham, R., and Langer, W. D.
1973, Ap. J., 179, 469.
-
Heathcote, S. R., and Brand, P. W. J. L.
1983, M.N.R.A.S., 203, 67.
-
Heckman, T. M.
1981, Ap. J. (Letters), 250, L59.
-
Heckman, T. M., Baum, S. A., van Breugel, W. J. M., and McCarthy, P.
1989, Ap. J., 338, 48.
-
Hogan, C. J.
1987, Ap. J. (Letters), 316, L59.
-
Hu, E. M., Cowie, L. L., and Wang, Z.
1985, Ap. J. Suppl.,
59, 447.
-
Ikeuchi, S., and Spitzer, L.
1984, Ap. J., 283, 825.
-
Johnstone, R. M., Fabian, A. C., and Nulsen, P. E. J.
1987, M.N.R.A.S., 224, 75.
-
Klein, R. I., McKee, C. F., and Colella, P. 1989, in
Evolution of the Interstellar Medium,
ed. L. Blitz (San Francisco: Astronomical Society of the Pacific), in press.
-
Krolik, J. H.
1988, Ap. J., 325, 148.
-
Krolik, J. H., McKee, C. F., and Tarter, C. B.
1981, Ap. J., 249, 422 (KMT).
-
Lepp, S., and Dalgarno, A.
1988, Ap. J., 335, 769.
-
Lepp, S., McCray, R., Shull, J. M., Woods, D. T., and Kallman, T.
1985, Ap. J., 288, 58.
-
Lynds, R.
1970, Ap. J. (Letters),
159, L151.
-
Mathews, W. G., and Bregman, J. N.
1978, Ap. J., 224, 308.
-
Mathews, W. G., and Ferland, G. J.
1987, Ap. J., 323, 456.
-
McCray, R. 1979, in
Active Galactic Nuclei,
ed. C. Hazard and S. Mitton (Cambridge: Cambridge U. Press), p. 227.
-
McCray, R. 1986, private communication.
-
McCray, R., and Kafatos, M. C.
1987, Ap. J., 317, 190.
-
McCarthy, P. J., van Breugel, W., Spinrad, H., and Djorgovski, S.
1987, Ap. J. (Letters),
321, L29.
-
McKee, C. F. 1988, in
Supernova Remnants and the Interstellar Medium, IAU
Colloq. 101,
ed. R. S. Roger and I. L. Landecker (Cambridge: Cambridge U. Press), p. 205.
-
McKee, C. F., and Begelman, M. C.
1990, Ap. J., 358, 392.
-
McKee, C. F., and Cowie, L. L.
1977, Ap. J., 215, 213.
-
McKee, C. F., and Ostriker, J. P.
1977, Ap. J., 218, 148.
-
Nittmann, J., Falle, S. A. E. G., and Gaskell, P. H.
1982, M.N.R.A.S., 201, 833.
-
Norman, C. A., and Ikeuchi, S.
1989, Ap. J., 345, 372.
-
Nulsen, P. E. J.
1982, M.N.R.A.S., 198, 1007.
-
Nulsen, P. E. J.
1986, M.N.R.A.S., 221, 377.
-
Penston, M. V., and Brown, F. E.
1970, M.N.R.A.S., 150, 373.
-
Raymond, J. C., Cox, D. P., and Smith, B. W.
1976, Ap. J., 204, 290.
-
Rees, M. J.
1988, M.N.R.A.S., 231, 91P.
-
Rees, M. J.
1989, M.N.R.A.S., 239, 1P.
-
Rees, M. J., and Ostriker, J. P.
1977, M.N.R.A.S., 179, 541.
-
Sarazin, C. L.
1986, Rev. Mod. Phys., 58, 1.
-
Scalo, J. M.
1977, Ap. J., 213, 705.
-
Shapiro, P. R., and Field, G. B.
1976, Ap. J., 205, 762.
-
Shull, J. M., and Woods, D. T.
1985, Ap. J., 288, 50.
-
Silk, J.
1977, Ap. J., 211, 638.
-
Spitzer, L.
1956, Ap. J., 124, 20.
-
Spitzer, L. 1962,
Physics of Fully Ionized Gases (New
York: wiley), 2n edition.
-
Spitzer, L. 1978,
Physical Processes in the Interstellar Medium
(New York: Wiley).
-
Spitzer, L.
1982, Ap, J., 262, 315.
-
Tarter, C. B., Tucker, W. H., and Salpeter, E. E.
1969, Ap. J., 156, 943.
-
Thomas, P.
1988, M.N.R.A.S., 235, 315.
-
Thomas, P. A., Fabian, A. C., and Nulsen, P. E. J.
1987, M.N.R.A.S., 228, 973.
-
Tribble, P. C.
1989, M.N.R.A.S.,
238, 1247.
-
Wang, Z., and Cowie, L. L.
1988, Ap. J., 335, 168.
-
Woodward, P.
1976, Ap. J., 207, 484.
-
Zel'dovich, Ya. B., and Pikel'ner, S. B.
1969, Sov. Phys. J.E.T.P., 29, 170.
-
Zweibel, E. G., and Josafatsson, K.
1983, Ap. J., 270, 511.
 INTRODUCTION
INTRODUCTION
 THEORY OF MULTIPHASE MEDIA
THEORY OF MULTIPHASE MEDIA
 Why thermal phases?
Why thermal phases?
 Connection with thermal instability
Connection with thermal instability
 Examples of thermal phases
Examples of thermal phases
 INTERACTIONS AMONG PHASES
INTERACTIONS AMONG PHASES
 Evaporation and condensation
Evaporation and condensation
 Ablation
Ablation
 Consequences of Mass Exchange
Consequences of Mass Exchange
 Mass exchange vs. radiative heating/cooling
Mass exchange vs. radiative heating/cooling
 Evolution of multiphase systems
Evolution of multiphase systems
 CONCLUSIONS
CONCLUSIONS
 REFERENCES
REFERENCES
 (n, T,
xj) is the heating rate per particle and
(n, T,
xj) is the heating rate per particle and
 (n,
T, xj)
is the cooling function, then the equation of thermal equilibrium may be
written
(n,
T, xj)
is the cooling function, then the equation of thermal equilibrium may be
written

 nj/n. The pressure is given by
p = xtnkT, where xt =
nj/n. The pressure is given by
p = xtnkT, where xt =
 xj is the
number of particles per hydrogen nucleus. An equation analogous
to (1) determines the ionization equilibrium.
xj is the
number of particles per hydrogen nucleus. An equation analogous
to (1) determines the ionization equilibrium.


 = 0 and this reduces
to Field's instability criterion
= 0 and this reduces
to Field's instability criterion

 s /
s /



 < n2, as shown in
< n2, as shown in


 c
c
 1 allows for a reduction in
the mean free path due to magnetic fields or turbulence. Equation (7) is
appropriate when
the electron mean free path is sufficiently short compared to
T / |
1 allows for a reduction in
the mean free path due to magnetic fields or turbulence. Equation (7) is
appropriate when
the electron mean free path is sufficiently short compared to
T / | T|
that heat conduction can be treated in the diffusion approximation,
T|
that heat conduction can be treated in the diffusion approximation,
 =
-
=
-
 )1/2
is the isothermal sound speed in the intercloud medium and
)1/2
is the isothermal sound speed in the intercloud medium and

 F is
the maximum length scale across which thermal
conduction can dominate over radiative heating and cooling. Therefore,
the thickness of a
conductive interface with a radius of curvature rc is
~ min(
F is
the maximum length scale across which thermal
conduction can dominate over radiative heating and cooling. Therefore,
the thickness of a
conductive interface with a radius of curvature rc is
~ min(
 psat, which was refined and generalized to spherical
clouds by
McKee and Begelman (1990).
psat, which was refined and generalized to spherical
clouds by
McKee and Begelman (1990).
 ab ~
ab ~
 r2c
r2c
 -1,
where
-1,
where 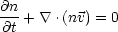
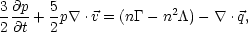
 r
for classical conduction) whereas that due to heating or cooling
is proportional to r3. Thus, there is a critical
length scale which enters the problem, which
turns out to be the Field length,
r
for classical conduction) whereas that due to heating or cooling
is proportional to r3. Thus, there is a critical
length scale which enters the problem, which
turns out to be the Field length,
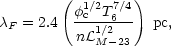

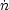 ev to define an
effective evaporative cooling rate,
ev to define an
effective evaporative cooling rate,
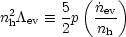
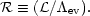
 M
M
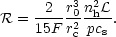
 '0 derived by
Cowie and McKee (1977),
with the result that
'0 derived by
Cowie and McKee (1977),
with the result that

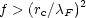
 2r0. In terms of the
sound-crossing time across rc (measured in the hot phase),
ts ~ rc / 2cs, and
the radiative cooling time in the hot phase,
tc ~ 5kTh / 2nh
2r0. In terms of the
sound-crossing time across rc (measured in the hot phase),
ts ~ rc / 2cs, and
the radiative cooling time in the hot phase,
tc ~ 5kTh / 2nh


 1.6 ×
10-19T-1/2 erg cm3
s-1 (105 K
< T < 4 × 107 K), multiplied by an
enhancement factor
1.6 ×
10-19T-1/2 erg cm3
s-1 (105 K
< T < 4 × 107 K), multiplied by an
enhancement factor

 10 to take account of
nonequilibrium ionization and density inhomogeneity near conduction fronts
(McKee and Ostriker 1977),
we have
10 to take account of
nonequilibrium ionization and density inhomogeneity near conduction fronts
(McKee and Ostriker 1977),
we have
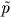 4
4
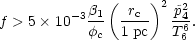
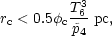

 104 K. The intercloud medium remains
thermally stable until radiative cooling begins to dominate over
evaporative cooling, at Th
104 K. The intercloud medium remains
thermally stable until radiative cooling begins to dominate over
evaporative cooling, at Th
 is
is



 = 0 in
eqs. (24) and (26), we obtain
= 0 in
eqs. (24) and (26), we obtain





